1. 介绍
点云配准(Point Cloud Registration)算法指的是输入两幅点云 Ps (source) 和 Pt (target),输出一个变换T(即旋转R和平移t)使得 T(Ps)和Pt的重合程度尽可能高。常用的有NDT、ICP。本文主要介绍ICP(Iterative Closest Point)算法及其各种变体。
点云配准首先要知道两组点云的匹配关系,对于视觉三维点来说,可以通过视觉特征匹配来获取,对于雷达点云,可以通过最近邻匹配来获取,关于匹配本文不深入介绍。
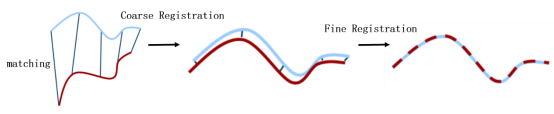
知道点云的匹配关系后,通过粗配准(Coarse Registration)和精配准(Fine Registration)两步来计算变换矩阵。粗配准指的是在两幅点云之间的变换完全未知的情况下进行较为粗糙的配准,目的主要是为精配准提供较好的变换初值;精配准则是给定一个初始变换,进一步优化得到更精确的变换。其中,粗配准存在解析解,精配准通过非线性优化的方式进一步优化结果。
2. 粗配准
粗配准目前来说还是一个难点。针对于不同的数据,有许多不同的方法被提出。
我们先介绍配准的评价标准,再在这个标准下提出一些搜索策略。
评价标准:比较通用的一个是LCP(Largetst Common Pointset)。给定两个点集P, Q,找到一个变换T(P),使得变换后的P与Q的重叠度最大。在变换后的P内任意一点,如果在容差范围内有另外一个Q的点,则认为该点是重合点。重合点占所有点数量的比例就是重叠度。
解决上述LCP问题,最简单粗暴的方法就是遍历。假设点集P, Q的大小分别为m, n。而找到一个刚体变换需要3对对应点。
那么 brute force 搜索的需要的复杂度。对于动辄几百万个点的点云,这种时间复杂度是不可接受的。
因此,许多搜索策略被提出。比较容易想到的是RANSAC之类的搜索方法。而对于不同的场景特点,可以利用需配准点云的特定信息加快搜索。(例如知道点云是由特定形状的面构成的)这里先介绍一个适用于各种点云,不需要先验信息的搜索策略,称为4PC(4 Point Congruent)。
搜索策略:4PC搜索策略是在P, Q中找到四个共面的对应点。
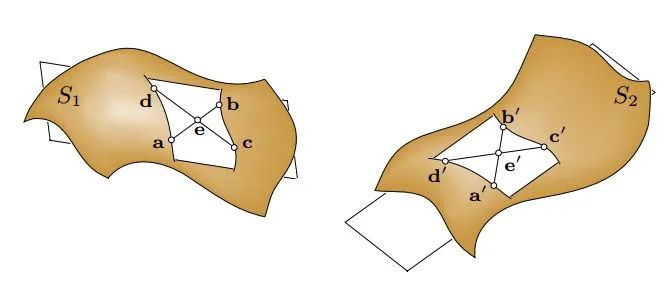
如上图所示(来自4PC原文),这四个共面的点相交于e。这里有两个比例在刚体变化下是不变的。(实际上在仿射变换下也是不变的)
![]()
而4PC将对于三个点的搜索转换为对ee'的搜索,从而将复杂度降低到了。
这四个点的距离越远,计算得到的转换越稳健。但是这里的四个点的搜索依赖于两个点云的重叠度。
4PC算法通用性较好,但是对于重叠度较小、或是噪声较大的数据也会出现配准错误或是运行时间过长的问题。针对于不同的场景很多其他的搜索策略也被提出。
3. 精配准
3.1. ICP算法
对于point-to-point ICP问题,最优变换是有解析解(closed-form solution)的,可以使用SVD 分解来计算。该解析解可以作为粗配准的结果。
3.1.1. SVD法
SVD法中求解旋转和平移是分开的。我们首先计算最优旋转,在根据最优结果计算最优平移。为了去除平移的影响,先将源点云和目标点云都转换到质心坐标下,即令
则点云配准问题的loss可以写为:
展开有:
因为点云是坐标是确定的,因此最小化loss转化为下式:
根据奇异值非负的性质和正交矩阵的性质(正交矩阵中的元素绝对值不大于 1),容易证得只有当M为单位阵时最大,即:
考虑到R为旋转矩阵的约束,最终解为:
自然地,最优平移可以得到:
3.1.2. 非线性优化法(迭代法)
我们发现,点对点的ICP问题存在最优解的解析解。但是仅使用解析解计算一次匹配误差还是比较大,这里可以采用迭代的方法次计算。每一次迭代我们都会得到当前的最优变换参数,然后将该变换作用于当前源点云;“找最近对应点”和“求解最优变换”这两步不停迭代进行,直到满足迭代终止条件,常用的终止条件有:
R, t的变化量小于一定值
loss 变化量小于一定值
达到最大迭代次数
3.2. PL(point-line)ICP算法(点到线)
点到点ICP算存在以下缺点:依赖初始值,初始值不好时,迭代次数增加;对于较大的初始误差,可能会出现错误的迭代结果;ICP是一阶收敛,收敛速度慢(为了弥补这一点,通常使用K-D树加快搜索);会有离群点及噪声。为此改善上述缺点,有人提出了PLICP,顾名思义,这种方式使用源点云到目标点云直线的距离度量来估计变换。主要区别在于误差函数的构建上。ICP是找最近邻的一点,以点与点之间的距离作为误差,而PLICP是找到最近邻的两点,两点连线,是以点到线的距离作为误差,实际上,后者的误差度量方式更符合结构化场景中的雷达点云的实际情况。因此具有更小的误差(图2)。然而,它对非常大的初始位移误差的鲁棒性较差,因此需要比较精确的初始值。
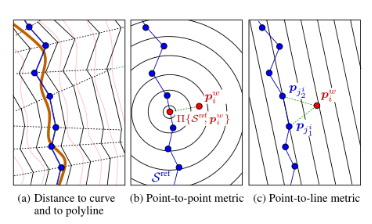
点到线的误差函数可以写为:
是目标点云中匹配到的最近两个点对应直线()的法线。作者设计了六个仿真实验,初始位移误差增加(均匀分布;从实验 1 中的 [±0.05m,±0.05m,±2°] 到实验 6 中的 [±0.2m,±0.2m,±45°])。对于每个实验,上述过程对 778 次扫描中的每一次重复 100 次。通过非线性优化的方式来求解点云的转换。这里给出算法的仿真结果:

3.3. Point-plane ICP
使用点到平面(point-plane)误差度量的迭代最近点 (ICP) 算法已被证明比使用点到点(point-point)误差度量的算法收敛得更快。在 ICP 算法的每次迭代中,产生最小点到平面误差的相对位姿变化通常使用标准的非线性最小二乘法来解决。例如 Levenberg-Marquardt 方法。当使用点到平面误差度量时,最小化的对象是每个源点与其对应目标点的切平面之间的平方距离之和(参见图 4)。

最小化损失函数可以写为:
其中是源点,是对应的目的点,是处的单位法线向量。这种方法的优缺点也很明显:首先,点到平面成本函数允许平坦区域相互滑动;点到平面通常比点到点收敛得更快;迭代次数更少 ;点到平面在每次迭代中速度较慢,并且需要表面法线。
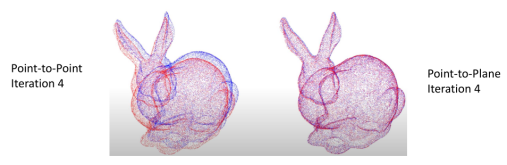
(8)式没有解析解,我们只能使用非线性最小二乘的方法求解,为了加快求解,有研究者发现当两个输入表面之间的相对方向较小时,可以使用近似的方法来有效地求解的线性最小二乘法近似非线性优化问题。
难以优化的原因是 R 太复杂,无法优化。在每次迭代中,我们假设旋转的角度很小,即

那么旋转矩阵可以近似表示为:

重写损失函数(8)为:
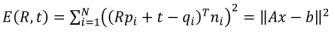
其中:

这样非线性的损失函数近似为线性,每一步迭代的最优解x为:

多次迭代后直到算法收敛。
3.4. NICP
Normal Iterative Closest Point (NICP)在匹配两组点云时,将点云的局部特征(法向量,曲率)考虑在内,即在迭代求解过程中,误差函数不仅包含点云之间的法向量的投影距离(同point to plane ICP),还包含了法向量方向误差。相比于上述的方法,NICP更加鲁棒。NICP 算法的特点在于,其在匹配两组点云时并非考虑匹配点云之间的欧氏距离,而是将点云曲面的局部特征作为点对匹配以及计算变换的准则。具体来说主要可以分为以下几部分:计算点云中每个点的特征,即其表面的的法向量(normal)和曲面曲率(curvature),以标记每个点;根据点的距离和特征找两组点云中的匹配点对;利用最小二乘法最小化,最小化目标函数,以求解点云变换矩阵。此处目标函数包括点面投影和法向量旋转误差。
令为带法线方向的三维点云,即T为由旋转矩阵R和平移向量t参数化的变换矩阵。具有法线的点的⊕算子是

则可以构造一个六维的误差函数:
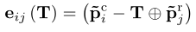
上述误差函数可以通过非线性优化的方法来求解,这里不再赘述
参考文献
4-Points Congruent Sets for Robust Pairwise Surface Registration
























 4万+
4万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








