1篇搞懂贝叶斯因果发现：如何用数据构建因果网络？理论详解与开源落地

贝叶斯方法正变得越来越流行，但初学者可能感到有些不知所措。这篇全面的指南将带您深入了解因果发现贝叶斯方法的应用、相关库及依赖项。

贝叶斯技术具有无限的可能性，这既是其优势，也带来挑战。由于其应用领域广泛，理解不同技术如何与具体解决方案和实际应用相关联，可能会让人感到困惑。

在本文中，我将带您了解贝叶斯方法的应用全景，并阐述不同的应用如何遵循不同的因果发现方法。换句话说，如何使用离散或连续数据集构建因果网络（即有向无环图）？在存在或不存在响应/处理变量的情况下，我们能否确定因果网络？针对特定问题，又该如何选择 PC、Hillclimbsearch 等搜索方法？

读完本文，您将对这些问题有所了解，知道从何处入手，以及如何为您的具体应用场景选择最合适的贝叶斯因果发现技术。希望这篇指南能帮助您更好地探索贝叶斯方法，请放松心情，享受阅读之旅。

简史回顾

在数据科学领域，贝叶斯方法正成为一股“新势力”。要预见贝叶斯领域未来的发展方向，了解其历史很有益处。您可能不会惊讶，贝叶斯统计学其实已经存在了相当长的时间。让我们从贝叶斯本人——精确地说，是托马斯·贝叶斯（Thomas Bayes）——开始。他在 1763 年发表的一篇论文 [[1]]中首次提出了 贝叶斯定理，这奠定了我们现在所知的基础。此后很长一段时间，贝叶斯方法几乎被遗忘，直到 20 世纪 50 年代到 60 年代马尔可夫链蒙特卡洛 (MCMC) 方法的发明。因此，MCMC 的发明至关重要，它提供了近似计算方法，使得在难以或无法获得精确解的情况下，仍能估计复杂的概率分布。

有趣的是，时间飞逝，距离贝叶斯最初提出理论已过去 261 年，我们依然在其原始工作的基础上不断构建新的方法。

什么是贝叶斯定理？

贝叶斯定理构成了贝叶斯网络的基础。贝叶斯规则本身用于更新模型信息，其公式如下：

公式：贝叶斯规则。图片作者自绘。

这个公式包含四种概率。让我们逐步分解它们。其中最常用的便是 先验概率 (prior)，也称为 信念概率 (belief probability)。它是基于已有知识或历史信息，在观察到证据之前对某一事件发生可能性的假设。例如，医生在实验室结果出来之前，根据患者的症状和年龄，可能会相信患者患有某种疾病的几率为 20%。或者在一个多云的日子，您相信下雨的几率有 80%，于是带着伞出门。 公式中的另一种概率是 条件概率 (conditional probability) 或称 似然 (likelihood)。这是在假设为真的条件下，出现证据的概率，这可以从数据中得出。接着是 边缘概率 (marginal probability)，它描述在所有可能的假设下出现新证据的概率，需要计算得出。最后是 后验概率 (posterior probability)，它是给定证据 X 发生时，Z 发生的概率。

漫漫流行之路

使用贝叶斯还是不使用，这是个问题。至今，关于 贝叶斯 方法与 频率学派 方法之间的争论仍在持续。哪种方法更好？ 首先，两种方法都能从信息（数据）的整体中发现模式。一个关键区别在于，只有贝叶斯统计能够纳入先验知识。这意味着可以预先包含某些假设，从而获得先发优势，并使分析更加可靠。这使得贝叶斯分析非常强大，尤其是在医学等领域，当存在关于疾病、人群和治疗的缺失数据，而医生拥有先验知识时，贝叶斯方法显得尤为重要。相比之下，频率学派方法需要提前选择实验设计，而贝叶斯分析则更加灵活，无需预先做出决定。

很长一段时间里，频率学派方法 占据主导地位，因为它们在大样本量下进行推断时计算相对容易，而贝叶斯方法则计算更复杂。我在 2010 年代初处理全基因组分子数据时深有体会。我当时试图对数千个特征（基因表达）建模，以分析与治疗相关的复杂因果关系。解决这个问题需要对高维概率分布进行复杂的积分运算。考虑到当时庞大的数据集和有限的计算能力，选择能够提供闭式解（closed-form solutions）的统计方法更为实际。这意味着当时利用贝叶斯技术，至少在计算能力有限的情况下，无法回答基因组层面的某些因果性问题。

贝叶斯技术现在开始受到关注！但我们还未完全摆脱困境。

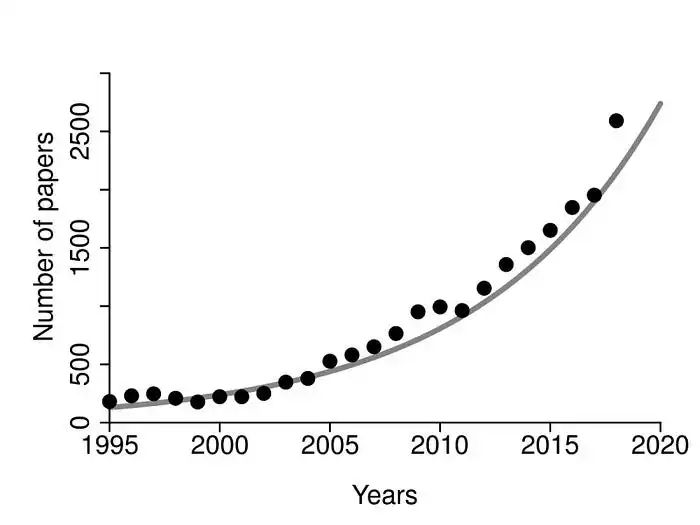1995 年至 2018 年期间，使用贝叶斯统计发表的医学文章数量。图片来源：https://www.ncbi.nlm.nih.gov/pmc/articles/PMC6406060/

近年来，计算能力飞速增长，这或许会充分激发贝叶斯技术的应用潜力。然而，挑战依然存在。尽管计算能力已大幅提升，但贝叶斯技术面临的新挑战在于如何有效地应用和解释贝叶斯统计结果。一般来说，任何技术、方法或统计数据，如果我们不知道如何正确使用、应用或解释它，都是毫无意义的。

尽管计算能力已大幅提升，但贝叶斯技术面临的新挑战在于如何有效地应用和解释贝叶斯统计结果。

贝叶斯思维的兴起

贝叶斯思维是一种自然的更新认知的方式，随着您收集更多数据，您的结论会变得更加准确。许多核心基本原理历经数百年形成，且大多源自学术界。然而，如今贝叶斯统计建模的框架正不断涌现，它们不仅来自开源社区，也有大型公司的贡献。因此，除了理论基础，我们正看到越来越多的框架问世。

我们正走向因果发现的“完美风暴”。我们拥有海量数据、可扩展的计算能力以及强大的贝叶斯分析框架。

近年来，许多行业都在努力实施 数据驱动的解决方案，其中机器学习解决方案是关键。如今，我们正逐步将其扩展到 数据驱动的决策制定。数据科学家认识到，将先验知识融入模型可以提高预测准确性并带来更好的结果，尤其是在可以进行干预以进一步优化的情况下。贝叶斯技术的例子包括改进统计推断、开发用于复杂决策的贝叶斯网络以及贝叶斯优化技术。在下一节中，我将介绍一些可以使用贝叶斯建模解决的实际应用问题。

因果发现的应用全景

贝叶斯统计学的应用全景可能相当复杂，因为它是一个总称，指代依赖于贝叶斯定理的广泛统计方法和途径。为了结构化地阐述，我将沿用数据科学领域常用的 监督 (supervised) 和 无监督 (unsupervised) 术语。值得注意的是，在贝叶斯语境下，这些术语并不常用，但我认为它们有助于理解，就像在机器学习中一样，进行受控实验并设定目标变量（即监督）并非总是可能或成本太高。从非受控或观测数据集中发现因果关系的方法（即无监督）很有价值，但它们与监督方法遵循不同的路径。因此，每个类别都有其独特的技术、方法和输入数据类型。在本节中，我将重点介绍一些可以使用贝叶斯建模解决的实际问题。大致来说，贝叶斯策略可以分为多个类别，其中包括：优化 (Optimization)、时间序列 (Time series)、因果发现（监督）和因果发现（无监督）。

贝叶斯应用的四个类别和相关库：时间序列、优化、监督式因果发现和无监督式因果发现。图片作者自绘。

贝叶斯优化

优化方法在许多应用中至关重要，因为它们能显著加速计算并减少计算负担。一个例子是 Bayesian-Optimization 库(https://github.com/bayesian-optimization/BayesianOptimization)，它试图在尽可能少的迭代次数内找到未知函数的最大值。另一个重要的优化应用是树形算法（如 XGBoost）中的网格搜索。使用暴力搜索方法确定最优超参数计算量和内存消耗巨大，而使用贝叶斯优化则可以高效地调优超参数。一个将传统网格搜索与贝叶斯优化相结合的库是 Hyperopt。该库包含三种优化算法：RandomSearch、Tree-Structured Parzen Estimators (TPEs) 和 Adaptive TPEs。然而，这些技术通常与具体方法无关，需要手动与目标模型集成。为了解决这个问题，Hyperopt 的整个优化策略与各种树形方法（如 XGBoost、lightGBM 和 Catboost）一起被集成到了 *Hgboost* 中。

贝叶斯时间序列

贝叶斯建模的第二个重要应用是估计干预措施随时间产生的因果效应。想象您是一位企业主，投放了一场营销活动后，销售额出现了增长。这太棒了，对吧？但问题是，这次增长是因为您的营销活动，还是由于季节性、天气等因素，仅仅是巧合？ 贝叶斯时间序列分析的作用正是在此。它能够帮助我们区分数据中的系统性变化与随机噪声。在这种情况下，它会估计营销活动的效果，并确定它是否是导致销售额随时间增长的因果因素。有多个库可以使用贝叶斯统计对随时间变化的趋势进行建模，其中两个知名的库是 PyMC 或 CausalImpact。CausalImpact 库使用贝叶斯结构时间序列模型，通过对给定干预的影响进行建模，来分析预期时间序列数据与观测时间序列数据之间的差异。而 PyMC 则可以处理因果推断、高斯过程、空间分析到时间序列分析等问题。以下表格列出了一些应用示例。

贝叶斯时间序列示例。表格作者自绘。

这些应用的共同点是，在一个现有流程或产品中引入了干预，这可能导致了随时间发生的变化。问题在于量化干预的因果效应。与其他所有方法一样，强有力的结论需要强有力的假设。因此，并非所有应用场景都适合使用贝叶斯方法，尤其是在量化主观结果（如“生产力”）或无形因素（如“员工士气”）时，往往面临较大困难。在这种情况下，由于混杂变量或难以将特定干预效果与其他影响隔离开来，精确衡量干预影响可能具有挑战性。

因果发现（监督式）

确定数据集中变量的因果效应可以分为两种方式，即第三和第四个类别。类似于机器学习方法，存在 监督式和无监督式方法。

在 监督式因果发现方法 中，您的数据集中有一个目标变量，并且（取决于用例）可能有一个处理变量。在监督式情境下，您就像一位侦探，带着明确的嫌疑人来到犯罪现场。您收集证据以确认或否定您的怀疑。这是一种受控的方式来审视因果关系。这种方法还提供了控制手段，以确定引入某些处理变量时结果是否会发生改变。一个很好的例子是 DoWhy 网站上描述的案例，他们旨在确定酒店预订取消的因果关系。这里的目标（或结果）变量是预订取消，但引入了一个处理变量“分配不同的房间”，以确定这是否能减少取消数量。可以对这类因果发现问题进行建模的知名库有 PyMC 和 DoWhy。这些库可以在给定结果变量和处理变量的情况下估计因果效应。以下表格列出了一些应用示例。在下一节中，我将更深入地探讨如何使用无监督方法进行因果发现。

监督式因果发现示例。表格作者自绘。

因果发现（无监督式）

发现因果关系的第四个类别是无监督贝叶斯方法。与监督式方法相比，这些方法更具挑战性。让我再次用您内心的侦探来解释这个问题，这位侦探想要找出因果关系。在无监督方法中，您来到犯罪现场，但没有任何嫌疑人。然而，现场留下了可能指向嫌疑人的线索（变量）。这意味着您需要调查线索的组合，以确定因果关系，这有助于您找到嫌疑人。 现在的问题是：您将如何处理现场留下的这一系列线索？ 也许是逐一独立检查，然后排除无效的？或者您会列出所有可能的组合，然后以结构化的方式逐一排查？因此，解决这个问题有多种方法。如果线索很少，追踪所有线索并查看它们是否指向嫌疑人相对容易。然而，当有数百或数千条线索时，追踪所有线索将变得非常耗时，甚至不可能。稍后我将演示，可能的组合数量会随着线索数量呈指数级增长。这使得在有太多线索时很难找到嫌疑人。幸运的是，有解决方案，因为您需要的是一种能够以巧妙方式遍历所有线索的 搜索策略。

无监督贝叶斯方法从大量变量中揭示隐藏的因果关系，而无需预设指导。挑战在于如何有效地遍历无数变量组合，识别潜在的因果联系。

无监督因果发现非常适合于没有受控实验但需要理解是否可以从非受控或观测数据中发现因果关系的情况。通过此类分析，可以进一步了解是否可以对因果因素进行干预。然而，如前所述，以无监督方式分析数据集是一项具有挑战性的任务，因为它没有响应变量或目标变量。此外，数据集可以是连续型、离散型或混合型，这带来了另一个挑战。

知名的无监督因果发现库有 Pgmpy，它包含低级别的统计函数，以及 Bnlearn 库，它包含了用于因果发现的即用型流程，形式为 结构学习、参数学习 和 概率推断。为了分解复杂性，我将逐步介绍三种方法：基于约束的方法、基于评分的方法 和 混合结构学习。在这些策略中，我将大量使用“结构学习”、“参数学习”和“概率推断”等术语。这些术语的定义如下：

• 结构学习：估计最能拟合数据集并捕获变量间依赖关系的有向无环图 (DAG)。
• 参数学习：给定数据集和 DAG，估计个体变量的（条件）概率分布。
• 概率推断：给定 DAG 和参数模型，计算查询的概率。

无监督因果发现的策略

无监督因果发现主要有三种策略：基于约束的方法 (Constraint-based)、基于评分的方法 (Score-based) 和 混合策略 (Hybrid Strategy)。下图描绘了这些策略以及与之相关的统计方法。每种策略都有一套特定的统计属性，并会产生一个因果网络。然而，就像机器学习中的无监督方法一样，选择合适的统计方法至关重要，因为因果发现网络的质量取决于统计方法与数据集属性的契合程度。别忘了，您还需要考虑用例的目标。这意味着您可能需要做出权衡。为了决定哪种统计方法最适合您的数据集和具体情况，我们需要理解这三种策略的属性和差异。请注意，下图描绘的策略是 BNlearn 库的一部分。这个框架提供了访问不同策略、搜索策略和评分函数的能力，将帮助您为用例选择最合适的模型。

无监督因果发现的应用全景。Bnlearn 库包含使用结构学习、参数学习和概率推断进行无监督因果发现的即用型流程。图片作者自绘。

1. 基于约束的方法 (PC)：在基于约束的策略中，如 PC (Peter-Clark) 算法，通过检验变量间的条件独立性来学习贝叶斯网络的结构。直观上，这种方法更像是一种经典的逻辑推理，通过演绎法来排除可能性。 例如，在洒水器数据集中，我们可以检验“下雨”和“洒水器开启”这两个事件在“多云”的条件下是否是条件独立的。如果它们是条件独立的，PC 算法就会移除“下雨”和“洒水器开启”之间的边。这种方法依赖于统计检验来确定两个变量在给定其他变量值的情况下是否相互独立。PC 算法首先在所有变量之间连接边（无向图），然后根据发现的条件独立性逐步移除变量之间的边。一旦确定了所有条件独立性，根据一套规则对无向边定向，形成有向无环图 (DAG)。PC 算法不依赖评分函数，而是侧重于数据中的条件独立性关系。
2. 基于评分的方法 (Score-based)：这种方法包含两个主要组件来确定最优的因果结果：搜索策略 和 评分函数。设定搜索策略和评分函数后，算法将在有向无环图 (DAG) 的整个空间中创建一个搜索路径，并使用评分函数评估每个 DAG。目标是找到得分最高的 DAG，这意味着它是在给定数据下最有可能的结构。换句话说，DAG 代表了基于数据的变量之间最佳的潜在依赖关系。DAG 中的每个节点对应一个变量，每个有向边代表变量之间的依赖关系（父节点到子节点的关系）。
3. 混合结构学习 (Hybrid structure learning)：混合结构学习方法结合了基于评分和基于约束这两种方法的元素。这些方法首先应用基于约束的技术，通过识别一些条件独立性来缩小搜索空间。一旦搜索空间缩小，再使用基于评分的方法来评估并选择最佳网络结构。混合方法旨在结合两者的优点：基于约束的方法能有效缩减潜在的 DAG 数量，而基于评分的方法则通过评估候选网络与数据之间的匹配水平进一步优化结构。这种组合可能更高效、更准确，特别是在包含数百个变量的数据集中，因为它同时利用了条件独立信息和评分函数。

无监督因果发现示例。表格作者自绘。

在下一节中，我将使用一些示例数据集来应用因果发现方法，并演示如何根据用例选择并应用不同的方法。

一个直观的无监督因果发现实际示例：基于评分的方法

为了直观地理解因果发现的概念，我们将通过一个实际示例来演示如何学习其结构，从经典的“洒水器数据集”开始。在这里，我们将先尝试创建所有可能的结构（即不使用搜索策略），然后对每一个进行评分。现在，想象您有一个花园，您想弄清楚草为什么会湿。您在过去 1000 天里测量了四个变量：“多云 (Cloudy)”、“洒水器 (Sprinkler)”、“下雨 (Rain)”和“湿草 (Wet Grass)”。每个变量有两种状态：“是”或“否”（如下图所示）。

对四个变量（洒水器、下雨、多云、湿草）测量 1000 天的数据。图片作者自绘。

如果我们能弄清楚这四个变量如何连接，就可以应用干预措施来防止草变湿。

在接下来的部分，我将通过实际示例演示如何根据数据集确定因果网络。我们将从包含四个变量的简单洒水器数据集开始，稍后也将探讨变量更多、数据类型（如类别型和连续型）不同的数据集。

# Install library
pip install bnlearn

# Load library
import bnlearn as bn

# Load sprinkler dataset
df = bn.import_example('sprinkler')
# Print to screen for illustration
print(df)
'''
+----+----------+-------------+--------+-------------+
|    |   Cloudy |   Sprinkler |   Rain |   Wet_Grass |
+====+==========+=============+========+=============+
|  0 |        0 |           0 |      0 |           0 |
+----+----------+-------------+--------+-------------+
|  1 |        1 |           0 |      1 |           1 |
+----+----------+-------------+--------+-------------+
|  2 |        0 |           1 |      0 |           1 |
+----+----------+-------------+--------+-------------+
| .. |        1 |           1 |      1 |           1 |
+----+----------+-------------+--------+-------------+
|999 |        1 |           1 |      1 |           1 |
+----+----------+-------------+--------+-------------+
'''

如何找到最优因果网络？

最优因果网络，换句话说，即有向无环图 (DAG)，代表了描述数据集中变量之间关系的最佳结构。为了演示目的，我们使用只有 4 个变量的洒水器数据集。一般来说，寻找因果 DAG 是一项具有挑战性的任务，因为可能的组合数量庞大。在我们的例子中，仅有四个变量，就已经有 543 种可能的 DAG。这意味着可以构建 543 种不同的网络，并且每一种都需要根据它与数据集的拟合程度进行评估。尽管您可能觉得 4 个节点应该只有更少的图，但其复杂性在于如何安排节点之间的有向边（同时确保没有环）。每对节点之间可能无边，或有从一个到另一个的有向边，或有相反方向的有向边（不形成环）。

总共有 543 个带有 4 个节点的唯一 DAG。图片作者自绘。

可以使用下面的公式计算给定节点数量 (n) 的可能 DAG 总数。总数 G(n) 是节点数 n 的函数，并且随 n 超指数增长。

计算给定节点数量 (n) 的可能 DAG 数量的公式。

如果我们计算不同节点数量下的总可能组合数，总数会随着节点数量呈指数级增长。例如，4 个节点会产生 543 种组合。当有 5 个节点时，组合数变为 29,281，依此类推。您可以在下面的代码块中亲自尝试这个运行示例。您会意识到这是一项计算量巨大的任务。

随着节点数量增加，可能的 DAG 数量呈指数增长。尝试使用代码块重复此练习。表格作者自绘。

import itertools

# Function to check if a graph is acyclic.
defis_acyclic(graph, n):
    visited = [False] * n
    rec_stack = [False] * n

    defvisit(v):
        if rec_stack[v]:
            returnFalse# Found a cycle
        if visited[v]:
            returnTrue# Already visited

        visited[v] = True
        rec_stack[v] = True

        for u inrange(n):
            if graph[v][u] andnot visit(u):
                returnFalse

        rec_stack[v] = False
        returnTrue

    returnall(visit(v) for v inrange(n) ifnot visited[v])

# Number of variables (nodes)
n = 4

# Generate all possible directed edges between the 4 variables
nodes = range(n)
edges = list(itertools.permutations(nodes, 2))  # All possible ordered pairs of nodes
total_graphs = 0

# Check all subsets of edges (2^number of possible edges)
for subset in itertools.product([0, 1], repeat=len(edges)):
    # Create the graph from the subset
    graph = [[0] * n for _ inrange(n)]
    for i, (u, v) inenumerate(edges):
        if subset[i]:
            graph[u][v] = 1# Add a directed edge

    # Check if the graph is acyclic
    if is_acyclic(graph, n):
        total_graphs += 1# Count the acyclic graphs

# Output the total number of acyclic graphs (DAGs)
print(f"Total number of possible DAGs for {n} variables: {total_graphs}")

要确定最佳因果 DAG，我们需要对每个 DAG 与数据集的拟合程度进行评分。一种朴素的方法是穷尽式地对所有可能的 DAG 进行评分，然后根据得分进行排名，最后选择得分最高的 DAG。这种方法并不少见，被称为 穷尽搜索 (exhaustive search)。其优点在于这种方法会评估每个 DAG，因此您可以确定地找到最佳解决方案（全局最优）。缺点是当变量数量超过少数几个时，所需的计算量巨大。因此，穷尽搜索仅建议用于变量数量较少的数据集。在下面的代码块中，我们将加载洒水器数据集，使用 exhaustive 方法，并对每个 DAG 进行评分。然后，我们可以绘制出最佳的 DAG。

pip install bnlearn
# Load libraries
import matplotlib.pyplot as plt
import bnlearn as bn

# Load sprinkler dataset
df = bn.import_example('sprinkler')

# Learn the DAG in data using Bayesian structure learning and return all possible DAGs:
model = bn.structure_learning.fit(df, methodtype='exhaustivesearch', scoretype='bic', return_all_dags=True)

# Compute edge weights using ChiSquare independence test.
# model = bn.independence_test(model, df, test='chi_square', prune=False)

# print adjacency matrix
print(model['adjmat'])
# target     Cloudy   Rain  Sprinkler  Wet_Grass
# source
# Cloudy      False   True       True      False
# Rain        False  False      False       True
# Sprinkler   False  False      False       True
# Wet_Grass   False  False      False      False
# 这个邻接矩阵展示了学习到的因果网络结构。矩阵中的 `True` 表示存在从行标签（source）指向列标签（target）的有向边。
# 例如，"Cloudy" 行的 "Rain" 列为 True，表示存在从 Cloudy 指向 Rain 的有向边。

# Plot the best DAG
G = bn.plot(model, interactive=False)

# Plot using graphiviz
dot = bn.plot_graphviz(model)

洒水器系统的最佳 DAG 示例。得分最高的 DAG 具有以下逻辑：湿草的概率取决于洒水器和下雨。洒水器开启的概率取决于多云。下雨的概率取决于多云。图片作者自绘。

上图中我们绘制了每个 DAG 的 BIC 得分。得分最高的 DAG 得分为 -1953，而得分最差的 DAG 得分约为 -2700。需要注意的是，这些分数仅在当前实验范围内具有相对意义，跨实验对比时需谨慎对待。既然我们了解了小规模数据集的处理方法，在下一节中，我将演示如何处理变量更多的数据集。请继续阅读！

针对包含大量变量的数据集：寻找最优因果网络

对于变量数量较少的数据集，通过穷举测试所有可能的 DAG 组合来发现有向无环图（DAG）是一种可行的方法。然而，在实际应用场景中，我们通常会处理包含 10 个以上变量的数据集，并且每个节点（变量）可能有多种状态。这意味着，由于计算负担过重，我们无法再对所有可能的 DAG 进行穷举测试。因此，我们需要一种搜索策略，能够高效地遍历整个 DAG 搜索空间，而无需逐一测试每个 DAG，从而找到最优解。目前存在多种可用于此任务的搜索策略，每种策略都有其独特的属性。

搜索策略能够高效地遍历整个 DAG 搜索空间，无需逐一测试每个 DAG，即可找到最优的 DAG。

接下来，让我们尝试使用一个中等到大型的数据集来实践这一方法。我们将加载 Alarm 监控系统数据集(https://archive.ics.uci.edu/dataset/11/alarm+monitoring+system) [7]，该数据集包含 37 个离散变量，每个变量都有 2 个或更多的状态。因此，全部可能的 DAG 数量巨大，形成的搜索空间是巨大的。我们不能再使用穷举搜索，而是需要一种智能的搜索策略。对于这类数据集（如 Alarm 监控系统数据集），*Hillclimbsearch* 是一个合适的例子，它是一种启发式搜索方法，执行贪婪的局部搜索。它从一个完全无连接的 DAG 开始，随后通过逐步调整单条边来最大化得分。搜索在达到局部最大值时停止。

# Load libraries
import matplotlib.pyplot as plt
import bnlearn as bn

# Load Alarm dataset
df = bn.import_example('alarm')

# Learn the DAG in data using hillclimbsearch and BIC
model = bn.structure_learning.fit(df, methodtype='hillclimbsearch', scoretype='bic')

# Compute edge weights using ChiSquare independence test.
model = bn.independence_test(model, df, test='chi_square', prune=False)

# Plot the best DAG
bn.plot(model, edge_labels='pvalue', params_static={'maxscale': 4, 'figsize': (15, 15), 'font_size': 14, 'arrowsize': 10})

# Plot using graphiviz
dot = bn.plot_graphviz(model)

# Store to pdf
# dotgraph.view(filename='bnlearn_alarm') # Uncomment to save PDF

这是使用 Hillclimbsearch 搜索策略和 BIC 评分函数在 Alarm 数据集上得到的最佳得分 DAG。边上的值是使用卡方检验确定的 -log10(P 值)。图由作者使用 Bnlearn 库创建。

至此，我们已经认识到，当变量数量较多时，搜索策略 是不可或缺的，它们能帮助我们在庞大的 DAG 搜索空间中高效地寻找最优解。此外，还需要一个 *评分函数* 来量化贝叶斯网络与数据集的拟合程度。将搜索策略与评分函数相结合的方法，被称为基于分数的方法（Score-based strategy）。在下一节中，我们将探讨使用不同搜索策略和评分函数时结果会有何差异。

改变搜索策略和评分函数会导致最终结果不同

在使用基于分数的方法进行因果发现时，最终的 DAG 将由所选择的搜索策略和评分函数的组合决定。这需要在速度和准确性之间取得平衡。因此，建议根据您的具体用例和数据集来选择合适的搜索策略和评分函数。

搜索策略

搜索策略是能够有效地遍历整个 DAG 搜索空间，最终找到最优 DAG，而无需逐一测试所有 DAG 的算法。每种方法都在复杂性、效率以及变量间依赖关系的表示准确性之间进行权衡。方法的选择取决于数据的大小和结构，以及手头的具体任务。

• ExhaustiveSearch (穷举搜索)：顾名思义，此方法评估所有可能的有向无环图（DAG），并选择得分最高的那个。虽然这能保证找到最优结构，但由于计算负担，它只能用于小型网络。换句话说，由于可能的 DAG 数量呈指数级增长，穷举搜索对于大型网络是不切实际的。如果您的计算机性能足够强大，典型的数据集大小上限约为 5 到 10 个节点。
• HillClimbSearch (爬山算法搜索)：这种启发式搜索策略适用于大型网络（在 Bnlearn 库中设为默认）。HillClimbSearch 使用贪婪的局部搜索算法，从一个完全无连接的 DAG 开始，然后通过迭代地进行单边更改来最大化分数。搜索在达到局部最大值时停止。因此，一个缺点是它可能无法总是找到全局最优解，因为它可能会陷入局部最优。此外，多次运行该方法得到的结果可能会有所不同。
• Chow-Liu Algorithm (Chow-Liu 算法)：此算法专门用于学习树形结构。它找到最大似然树，其中每个节点最多只有一个父节点。Chow-Liu 算法非常高效，因为其复杂性受限于其仅限于树形结构的特点，使其成为处理更简单依赖模型的理想选择。此外，设置根节点参数是可选的，这使您可以控制 DAG 的起始点，这对于某些用例可能很方便。
• Tree-Augmented Naive Bayes (TAN) (树增强朴素贝叶斯)：TAN 算法是基于树的方法的扩展，可以检索更复杂的关系。它对于具有许多相互依赖变量的大型数据集特别有用。TAN 通过用额外的基于树的依赖关系增强朴素贝叶斯模型，从而允许结构具有一定的灵活性，因此可以在保持计算效率的同时捕获更错综复杂的关系。这种搜索策略需要设置根节点参数，这迫使您从 DAG 中的某个特定节点开始。在某些用例中，这可能不受欢迎。
• Naive Bayes (朴素贝叶斯)：朴素贝叶斯是最简单的概率模型形式。假设在给定类别标签（或目标变量）的情况下，每个变量都与其他所有变量条件独立。虽然这个假设在真实世界的数据中很少成立，但朴素贝叶斯对于分类任务，特别是当特征之间的依赖关系较弱或需要快速、高效的模型时，对于大型数据集的效果出奇地好。然而，它无法表示变量之间的相互依赖关系，因此在建模复杂关系方面不如上述方法灵活。这种搜索策略也需要设置根节点参数，这迫使您从 DAG 中的某个特定节点开始。同样，在某些用例中，这可能不受欢迎。
• Direct-LiNGAM: 这种方法专门用于使用半参数方法建模连续和混合数据集。它假设观测变量之间存在线性关系，同时确保误差项遵循非高斯分布，并限制图必须是无环的。
• ICA-LiNGAM: 这种方法专门用于从数据集中估计因果图。它基于变量遵循具有非高斯噪声的线性模型的假设。该方法基于以下假设：数据集具有非高斯噪声，噪声在变量之间是独立的，并且不存在未观测的混杂因素。

搜索策略概述与对比。图由作者创建。

评分函数

评分函数量化了特定 DAG 解释观测数据的优劣程度。列出的评分函数是众所周知的，理解它们的特性将帮助您为您的用例仔细选择最合适的搜索策略和评分函数。

• Bayesian Information Criterion (BIC) (贝叶斯信息准则)：BIC 平衡了模型的拟合优度和复杂性。它通过惩罚具有更多边的 DAG 来避免过拟合。
• Bayesian Dirichlet Equivalent Uniform (BDeu) Score (贝叶斯狄利克雷等效均匀分数)：此分数基于贝叶斯统计，使用 Dirichlet 分布作为概率表的先验分布。多项分布用于模拟离散类别结果的概率。观测数据后，后验分布也将遵循 Dirichlet 分布。这简化了在具有离散变量的贝叶斯网络中信念的更新和后验概率的计算过程。
• The K2 score (K2 分数)：此分数假设对可能的网络结构使用均匀先验。它通过根据变量之间的父子关系估计观测数据的可能性来评估给定网络的拟合度。与使用特定先验（如 Dirichlet）的方法不同，K2 方法通过假设父节点之间独立来简化过程，从而使概率计算更易于处理。这种方法在不需要详细的变量先验分布的情况下高效地找到良好的网络结构。
• The BDS score (贝叶斯狄利克雷结构分数)：贝叶斯狄利克雷结构（BDS）分数通过纳入关于网络结构的先验知识来扩展 BDeu 分数。它像 BDeu 一样假设 Dirichlet 先验，但也包括了对可能的有向无环图（DAGs）的先验。这使得它在您对变量之间的关系或网络结构约束有一定领域知识时非常有用。BDS 分数平衡了数据的拟合度、网络的复杂性和先验结构的强度。通过结合参数和结构的先验，BDS 可以得到更准确和更适合的模型，特别是对于中小型数据集。
• The AIC score (赤池信息准则)：赤池信息准则（AIC）是一种频率派方法，它通过惩罚模型中参数的数量来平衡拟合优度和模型复杂性。它是根据模型的最大似然估计以及对自由参数数量的惩罚来计算的，更复杂的模型会受到更高的惩罚。与 BIC 在大型数据集中倾向于选择更简单的模型不同，AIC 对复杂性的惩罚没那么严格，因此更有可能选择具有更多参数的模型。当数据集很大且是连续型数据，并且模型简单性不是主要考虑因素时，通常更倾向于使用 AIC。

评分函数。图由作者创建。

连续和混合数据集的因果发现

到目前为止，我们已经看到了适用于离散数据集的基于分数的方法。然而，现实世界的场景常常包含连续变量。当数据集包含连续变量和/或混合变量时，学习 DAGs 大致有三种不同的方式。每种方式都有其自身的优缺点。处理连续/混合数据集的三种方法如下：

1. 使用领域知识手动离散化连续数据集，然后使用贝叶斯方法。
2. 自动离散化连续数据集，然后使用贝叶斯方法。
3. 使用贝叶斯方法直接建模连续和混合数据集。

1. 先手动离散化连续变量进行因果发现

基于领域知识手动离散化连续变量是最直接的方法。然而，这可能也是最费力的方法，因为它需要根据对数据背景的理解，将连续数据转换为一组离散区间。此外，这可能还需要考虑变量之间的关系，这会增加额外的复杂性。不过，如果离散化做得准确，将会产生反映真实世界属性的有意义的数据点分组，并可以提高模型的解释性。为了演示，我将加载 auto_mpg 数据集(https://archive.ics.uci.edu/dataset/9/auto+mpg) [8]，该数据集来源于 UCI 机器学习库。例如，我们可以根据真实世界的意义定义马力类别：

• 低 (Low)： 马力小于 100 的汽车（小型、燃油效率高的汽车）
• 中 (Medium)： 马力在 100 到 150 之间的汽车（性能适中的汽车）
• 高 (High)： 马力高于 150 的汽车（高性能汽车）

该数据集包含 392 个样本和 6 个变量，如下面的代码块所示。

# Libraries
import pandas as pd
import datazets as ds # Note: datazets was imported but not used in this block.
import bnlearn as bn

# Download dataset
df = pd.read_csv('http://archive.ics.uci.edu/ml/machine-learning-databases/auto-mpg/auto-mpg.data-original',
                 delim_whitespace=True, header=None,
                 names = ['mpg', 'cylinders', 'displacement', 'horsepower', 'weight', 'acceleration', 'model year', 'origin', 'car name'])

# Cleaning
df.dropna(inplace=True)
df.drop(['model year', 'origin', 'car name'], axis=1, inplace=True)

# Show dataset head
print(df.head())

#     mpg  cylinders  displacement  horsepower  weight  acceleration
# 0  18.0        8.0         307.0       130.0  3504.0          12.0
# 1  15.0        8.0         350.0       165.0  3693.0          11.5
# 2  18.0        8.0         318.0       150.0  3436.0          11.0
# 3  16.0        8.0         304.0       150.0  3433.0          12.0
# 4  17.0        8.0         302.0       140.0  3449.0          10.5
#
# [392 rows x 6 columns]


# Define horsepower bins based on domain knowledge
bins = [0, 100, 150, df['horsepower'].max()]
labels = ['low', 'medium', 'high']

# Discretize horsepower using the defined bins
df['horsepower_category'] = pd.cut(df['horsepower'], bins=bins, labels=labels, include_lowest=True)

print(df[['horsepower', 'horsepower_category']].head())
#    horsepower horsepower_category
# 0       130.0              medium
# 1       165.0                high
# 2       150.0              medium
# 3       150.0              medium
# 4       140.0              medium

有时，您可以像处理汽缸数一样，通过将连续值转换为整数来轻松实现分类。

# Set the cylinder to integers
df['cylinders'] = df['cylinders'].astype(int)

将所有连续变量分类后，即可应用常规的结构学习过程。

# Structure learning
model = bn.structure_learning.fit(df, methodtype='hc')

# Compute edge strength
model = bn.independence_test(model, df)

# Make plot and put the -log10(pvalues) on the edges
bn.plot(model, edge_labels='pvalue')
dotgraph = bn.plot_graphviz(model, edge_labels='pvalue')
# dotgraph # Display graphviz plot (optional)

2. 通过自动离散化连续变量进行因果发现

与手动离散化变量相反，我们也可以自动确定每个变量的最佳分箱。然而，与手动分箱方法相比，此类方法需要额外注意，因为自动生成的区间可能不对应于有意义的领域特定边界。为了自动创建比简单的等宽或等频分箱更有意义的箱，我们可以确定最适合数据的分布，然后使用 95% 置信区间来创建低、中、高类别。

此外，通过分布图对创建的分箱进行可视化检查是明智的。通过这种方式，您可以判断低端、中端和高端是否是有意义的阈值。例如，如果我们以acceleration（加速度）为例，并执行自动分箱方法，我们会发现低端为 8 秒到约 11 秒，这将代表快速汽车。高端则是加速度为 20 秒到 24 秒的慢速汽车。其余汽车则属于normal（普通）类别。这似乎非常合理，因此我们可以继续使用这些类别。参见下面的代码块。

# Install library
pip install distfit
# Import library
from distfit import distfit

# Initialize and set 95% CII
dist = distfit(alpha=0.05)

# Fit Transform
dist.fit_transform(df['acceleration'])

# Make plot
dist.plot()
plt.show()
bins = [df['acceleration'].min(), dist.model['CII_min_alpha'], dist.model['CII_max_alpha'], df['acceleration'].max()]

# Discretize acceleration using the defined bins
df['acceleration_category'] = pd.cut(df['acceleration'], bins=bins, labels=['fast', 'normal', 'slow'], include_lowest=True)
del df['acceleration']

使用 distfit 进行概率密度拟合。图由作者创建。

如果存在多个连续变量，我们也可以自动化分布拟合的过程：

# For all remaining continuous columns, the same approach can be performed:
cols = ['mpg', 'displacement', 'weight']

# Do for every variable
for col in cols:
    # Initialize and set 95% CII
    dist = distfit(alpha=0.05)
    dist.fit_transform(df[col])

    # Make plot
    dist.plot()
    plt.show()
    bins = [df[col].min(), dist.model['CII_min_alpha'], dist.model['CII_max_alpha'], df[col].max()]

    # Discretize the variable in loop using the defined bins
    df[col + '_category'] = pd.cut(df[col], bins=bins, labels=['low', 'medium', 'high'], include_lowest=True)
    del df[col]

将所有连续变量分类后，即可应用结构学习的因果发现方法。

# Structure learning
model = bn.structure_learning.fit(df, methodtype='hc')

# Compute edge strength
model = bn.independence_test(model, df)

# Make plot and put the -log10(pvalues) on the edges
bn.plot(model, edge_labels='pvalue')

dotgraph = bn.plot_graphviz(model, edge_labels='pvalue')
# dotgraph # Display graphviz plot (optional)

这是使用 Hillclimbsearch 和 BIC 评分函数对 Auto mpg 数据集进行的最佳得分 DAG。所有连续值都已自动离散化。Distfit 用于确定 95% 置信区间，检查分布图并使用相应的类别。边上的值是使用卡方检验确定的 -log10(P 值)。图由作者使用 Bnlearn 创建。

3. 通过建模连续变量进行因果发现（概念验证）

使用离散化方法具有重要意义，因为它使得可以应用多种贝叶斯统计方法。然而，并非总是能够或期望对变量进行离散化。也有直接建模连续数据集的方法，例如 Bnlearn 中也实现的 LiNGAM 方法。

Direct-LiNGAM 方法是一种半参数方法，假设观测变量之间存在线性关系，同时确保误差项遵循非高斯分布，并限制图必须是无环的。此方法涉及重复使用线性回归（最小二乘法）进行回归分析和独立性评估，其中在每次回归中，一个变量作为因变量，另一个作为自变量。该过程将应用于变量对。换句话说，lingam-direct 方法允许您建模连续和混合数据集。一个缺点是，使用此方法时，因果发现的结构学习是最终目标，因此无法执行参数学习和概率推断。

为了演示其工作原理，我们将创建一个包含六个变量的玩具示例数据集。此数据集的目标是展示不同变量之间的因果关系及其影响。样本大小设置为 n=1000，连续值采用均匀分布。我们将引入变量间的依赖关系，然后使用模型推断原始值。

• 步骤 1：x3 是根节点，使用均匀分布初始化。
• 步骤 2：x0 和 x2 通过乘以 x3 的值创建，使其依赖于 x3。
• 步骤 3：x5 通过乘以 x0 的值创建，使其依赖于 x0。
• 步骤 4：x1 和 x4 通过乘以 x0 和 x2 的值创建，使其依赖于 x0 和 x2。

实验 DAG 及其边上的因果值。图由作者使用 Bnlearn 创建。

import numpy as np
import pandas as pd
from lingam.utils import make_dot

# Number of samples
n=1000

# step 1
x3 = np.random.uniform(size=n)
# step 2
x0 = 3.0*x3 + np.random.uniform(size=n)
x2 = 6.0*x3 + np.random.uniform(size=n)
# step 3
x5 = 4.0*x0 + np.random.uniform(size=n)
# step 4
x1 = 3.0*x0 + 2.0*x2 + np.random.uniform(size=n)
x4 = 8.0*x0 - 1.0*x2 + np.random.uniform(size=n)
df = pd.DataFrame(np.array([x0, x1, x2, x3, x4, x5]).T ,columns=['x0', 'x1', 'x2', 'x3', 'x4', 'x5'])
print(df.head())

#     x0        x1       x2        x3        x4       x5
# 0  2.865624  8.403974  5.399000  0.954014  0.103734  3.544251
# 1  2.404482  9.233459  6.151153  0.751395 -3.048335  2.497600
# 2  2.812196  9.620275  5.780936  0.896724  2.637764  3.656403
# 3  1.237378  5.663474  3.611720  0.376238 -2.701573  1.884125
# 4  0.785370  3.883610  1.893362  0.167213  4.517477  0.984133

# Define the ground truth adjacency matrix for make_dot (not used in structure learning itself)
m = np.array([[0.0, 0.0, 0.0, 3.0, 0.0, 0.0],
              [3.0, 0.0, 2.0, 0.0, 0.0, 0.0],
              [0.0, 0.0, 0.0, 6.0, 0.0, 0.0],
              [0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
              [8.0, 0.0,-1.0, 0.0, 0.0, 0.0],
              [4.0, 0.0, 0.0, 0.0, 0.0, 0.0]])

# Use make_dot to visualize the ground truth DAG (optional, shown in original)
# dot = make_dot(m)
# dot # Display the ground truth DAG visualization

可以使用 direct-lingam 方法应用结构学习。

# Load library
import bnlearn as bn

# Structure learning
model = bn.structure_learning.fit(df, methodtype='direct-lingam')

查看学习到的邻接矩阵（即因果图结构）时，可以看到各种变量的依赖关系值得到了很好的恢复。

print(model['adjmat'])
# target        x0        x1       x2   x3        x4       x5
# source
# x0      0.000000  2.987320  0.00000  0.0  8.057757  3.99624
# x1      0.000000  0.000000  0.00000  0.0  0.000000  0.00000
# x2      0.000000  2.010043  0.00000  0.0 -0.915306  0.00000
# x3      2.971198  0.000000  5.98564  0.0 -0.704964  0.00000
# x4      0.000000  0.000000  0.00000  0.0  0.000000  0.00000
# x5      0.000000  0.000000  0.00000  0.0  0.000000  0.00000

使用卡方检验计算边强度。注意：此处使用 prune=False。

# Compute edge strength with the chi_square test statistic. Note: prune=False is used here.
model = bn.independence_test(model, df, test='chi_square', prune=False)

通过查看模型的 causal_order 属性，我们可以看到因果发现的结果排序。

print(model['causal_order'])
# ['x3', 'x0', 'x5', 'x2', 'x1', 'x4']

我们可以使用 utility function 绘制因果图。

# We can draw a causal graph using the utility function.
bn.plot(model)

下面的 DAG 展示了最终结果，不仅正确捕获了因果网络，还准确恢复了最初用于生成因果图的数值。

使用 Bnlearn 估计的因果图很好地表示了最初创建的 DAG。图由作者使用 Bnlearn 创建。

4. 使用 Auto MPG 数据集进行连续数据集的因果发现

最后一个例子，我们将再次加载 auto mpg 数据集，但这次我们将直接对连续变量进行建模，而不是离散化。对于这种方法，我们将把方法设置为 direct-lingam，然后在 bnlearn 中运行结构学习（Structure Learning）方法。

import bnlearn as bn

# Load example mixed dataset
df = bn.import_example(data='auto_mpg')
del df['origin']

# Structure learning or causal discovery
model = bn.structure_learning.fit(df, methodtype='direct-lingam', params_lingam = {'random_state': 2})

# Make plot (optional, before pruning)
# bn.plot(model)

# Compute edge strength with the chi_square test statistic
# prune=True will remove edges based on statistical significance
model = bn.independence_test(model, df, test='chi_square', prune=True)

############
# Plotting #
############
# Plot the pruned graph
bn.plot(model)
# bn.plot(model, edge_labels='pvalue'); # Redundant plot call

# Create interactive plot
# bn.plot(model, interactive=True) # Uncomment to enable interactive plot

# Create graphviz plot
dotgraph = bn.plot_graphviz(model)
# dotgraph # Display graphviz plot

# Create pdf
# dotgraph.view(filename='auto_mpg_bnlearn.pdf') # Uncomment to save PDF

# Create graphviz plot with Pvalue on the edges
dotgraph2 = bn.plot_graphviz(model, edge_labels='pvalue')
# dotgraph2 # Display graphviz plot with p-values

因果发现或结构学习的结果如下图所示。注意，此处绘制的是经过剪枝（prune=True）后的网络结构，即移除了统计上不显著的边。

使用 Bnlearn 中的 Direct-Lingam 方法对连续型 auto mpg 数据集进行因果发现。图 A 显示了边上的权重。图 B 显示了连接的两个变量之间的统计显著性（使用 -Log10(P 值)）。图由作者使用 Bnlearn 创建。

如何学习大模型 AI ？

由于新岗位的生产效率，要优于被取代岗位的生产效率，所以实际上整个社会的生产效率是提升的。

但是具体到个人，只能说是：

“最先掌握AI的人，将会比较晚掌握AI的人有竞争优势”。

这句话，放在计算机、互联网、移动互联网的开局时期，都是一样的道理。

我在一线互联网企业工作十余年里，指导过不少同行后辈。帮助很多人得到了学习和成长。

我意识到有很多经验和知识值得分享给大家，也可以通过我们的能力和经验解答大家在人工智能学习中的很多困惑，所以在工作繁忙的情况下还是坚持各种整理和分享。但苦于知识传播途径有限，很多互联网行业朋友无法获得正确的资料得到学习提升，故此将并将重要的AI大模型资料包括AI大模型入门学习思维导图、精品AI大模型学习书籍手册、视频教程、实战学习等录播视频免费分享出来。

第一阶段（10天）：初阶应用

该阶段让大家对大模型 AI有一个最前沿的认识，对大模型 AI 的理解超过 95% 的人，可以在相关讨论时发表高级、不跟风、又接地气的见解，别人只会和 AI 聊天，而你能调教 AI，并能用代码将大模型和业务衔接。

• 大模型 AI 能干什么？
• 大模型是怎样获得「智能」的？
• 用好 AI 的核心心法
• 大模型应用业务架构
• 大模型应用技术架构
• 代码示例：向 GPT-3.5 灌入新知识
• 提示工程的意义和核心思想
• Prompt 典型构成
• 指令调优方法论
• 思维链和思维树
• Prompt 攻击和防范
• …

第二阶段（30天）：高阶应用

该阶段我们正式进入大模型 AI 进阶实战学习，学会构造私有知识库，扩展 AI 的能力。快速开发一个完整的基于 agent 对话机器人。掌握功能最强的大模型开发框架，抓住最新的技术进展，适合 Python 和 JavaScript 程序员。

• 为什么要做 RAG
• 搭建一个简单的 ChatPDF
• 检索的基础概念
• 什么是向量表示（Embeddings）
• 向量数据库与向量检索
• 基于向量检索的 RAG
• 搭建 RAG 系统的扩展知识
• 混合检索与 RAG-Fusion 简介
• 向量模型本地部署
• …

第三阶段（30天）：模型训练

恭喜你，如果学到这里，你基本可以找到一份大模型 AI相关的工作，自己也能训练 GPT 了！通过微调，训练自己的垂直大模型，能独立训练开源多模态大模型，掌握更多技术方案。

到此为止，大概2个月的时间。你已经成为了一名“AI小子”。那么你还想往下探索吗？

• 为什么要做 RAG
• 什么是模型
• 什么是模型训练
• 求解器 & 损失函数简介
• 小实验2：手写一个简单的神经网络并训练它
• 什么是训练/预训练/微调/轻量化微调
• Transformer结构简介
• 轻量化微调
• 实验数据集的构建
• …

第四阶段（20天）：商业闭环

对全球大模型从性能、吞吐量、成本等方面有一定的认知，可以在云端和本地等多种环境下部署大模型，找到适合自己的项目/创业方向，做一名被 AI 武装的产品经理。

• 硬件选型
• 带你了解全球大模型
• 使用国产大模型服务
• 搭建 OpenAI 代理
• 热身：基于阿里云 PAI 部署 Stable Diffusion
• 在本地计算机运行大模型
• 大模型的私有化部署
• 基于 vLLM 部署大模型
• 案例：如何优雅地在阿里云私有部署开源大模型
• 部署一套开源 LLM 项目
• 内容安全
• 互联网信息服务算法备案
• …

学习是一个过程，只要学习就会有挑战。天道酬勤，你越努力，就会成为越优秀的自己。

如果你能在15天内完成所有的任务，那你堪称天才。然而，如果你能完成 60-70% 的内容，你就已经开始具备成为一名大模型 AI 的正确特征了。

这份完整版的大模型 AI 学习资料已经上传CSDN，朋友们如果需要可以微信扫描下方CSDN官方认证二维码免费领取【保证100%免费】