7 Brown运动

7.1 基本概念与性质

• 粒子在直线上随机游
• 单位时间向左向右一单位
• 现加速,在越来越小的时间间隔中走越来越小$\Delta x$
• 若以正确方式趋于极限,就得Brown
• 令每隔$\Delta t$时间等概率向左或向右移$\Delta x$
• $X(t)$：粒子的位置,则
  $$X(t)=\Delta x(X_1+...+X_{[t/\Delta t]})\text{\hspace{1em}(7.1.1)}$$
• 令$X_i$
• 1,右
• -1,左
• $X_i$相互独立
• 概率各1/2

 

• $E{X}_i=0$,$var(X_i)=E(X_i^2)=1$
• 有$E[X(t)]=0$
• $var[X(t)]=(\Delta x{)}^2(t/\Delta t)$
• 现令$\Delta x$和$\Delta t$趋于零
• 并使极限有意义
• 取$\Delta x=\Delta t$,令$\Delta \to 0$,则$var[X(t)]\to 0$,从而$X(t)=0$,a.s…
• 如果$\Delta x=\Delta t^3$,则$var[X(t)]\to \infty$
  • 不合理,粒子的运动是连续的,不可能短时间远离出发点
• so设:$\Delta x=\sigma \sqrt{\Delta t}$。$\sigma$为某个正常数
• 从上面的讨论可见,当$\Delta \to 0$时,$E[X(t)]=0$, $var[X(t)]\to {\sigma }^{2}t$

 

• 这一极限过程的直观性质
• 均值0,方差${\sigma }^{2}t$正态
• 随机游动的值在不相重叠的时间区间中的变化是独立的
  • { X ( t ) , t ≥ 0 } \{X(t),t≥0\} {X(t),t≥0}有独增
• 随机游动在任一时间区间中的位置变化的分布只依赖于区间的长度,可见
  • { X ( t ) , t ≥ 0 } \{X(t),t≥0\} {X(t),t≥0}有平稳增量

 

• Brown运动严格定义（定义7.1）
• { X ( t ) , t ≥ 0 } \{X(t),t\ge 0\} {X(t),t≥0}
  • $X(0)=0$
  • 独立的平稳增量
  • $X(t)\sim N(0,{\sigma }^{2}t)$
• 标准 Brown运动
• 不失一般性,只考标准

 

• 这一定义在应用中不方便
• 给出下面的性质作为Brown运动的等价定义

 

• 性质7.1
• $B(t)-B(s)\sim N(0,t-s)$
• 独增
• $B(t),t\ge 0$是$t$连续

 

• 注7.1
• 性质7.1没假定$B(0)=0$,称为始于$x$的Brown
  • 有时为强调起始点,记为 { B x ( t ) } \{B^x(t)\} {Bx(t)}
  • 定义7.1指的就是始于0
• 易见
  $$B^x(t)-x=B^0(t)\text{\hspace{1em}(7.1.2)}$$
• 式(7.1.2)按照下面的定义7.2称为 Brown运动的空间齐次性.
• 此性质也说明,$B^x(t)$和$x+B^0(t)$是相同的,
• 只需研究始于0的Brown就行
• 如不加说明,Brown就指始于0的

 

• 定义7.2
• 如果它的有限维分布是空间平移不变的
  P { X ( t 1 ) ≤ x 1 , X ( t 2 ) ≤ x 2 , . . . , X ( t n ) ≤ x n ∣ X ( 0 ) = 0 } P\{X(t_1)\le x_1,X(t_2)\le x_2,...,X(t_n)\le x_n|X(0)=0\} P{X(t1​)≤x1​,X(t2​)≤x2​,...,X(tn​)≤xn​∣X(0)=0}
  = P { X ( t 1 ) ≤ x 1 + x , X ( t 2 ) ≤ x 2 + x , . . . , X ( t n ) ≤ x n + x ∣ X ( 0 ) = x } =P\{X(t_1)\le x_1+x,X(t_2)\le x_2+x,...,X(t_n)\le x_n+x|X(0)=x\} =P{X(t1​)≤x1​+x,X(t2​)≤x2​+x,...,X(tn​)≤xn​+x∣X(0)=x}
• 称此过程为空间齐次

 

• 例7.1

 

• 利用独增及转移概率密度,可计算任意有限维分布

 

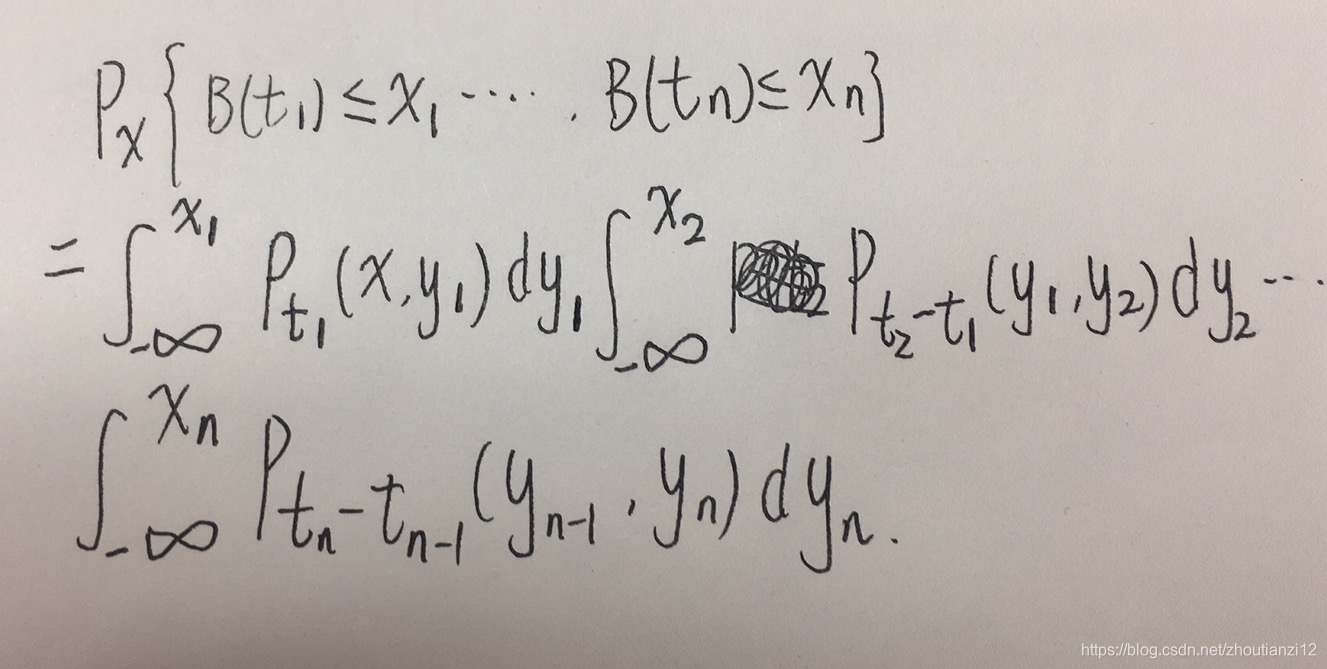
• 定义7.3
• Brown的二次变差$[B,B](t)$
• { t i n } i = 0 n \{t_i^n\}_{i=0}^n {tin​}i=0n​遍取$[0,t]$的分割,且${\delta }_n=\underset{0\le i\le n-1}{\max }(t_{i+1}^n-t_i^n)\to 0$时依概率收敛意义下的极限
  $$[B,B](t)=[B,B]([0,t])=$$
  $$\underset{{\delta }_n\to 0}{\lim }\sum _{i=0}^{n-1}|B(t_{i+1}^n)-B(t_i^n){|}^2\text{\hspace{1em}(7.1.5)}$$

Brown路径性质

• 从$0$到$T$对Brown的次观察称Brown$[0,T]$上的一路径或实现
  • 是$t$的函数
• Brown几乎所有路径$B(t)0\le t\le T$都
  • 是t的连续
  • 任何区间(无论多小)都不单调
  • 任何点都不可微
  • 任何区间(无论多小)上都是无限变差的;
  • $[0,t]$上的二次变差等于t.
• 1~3不难,4可从5得到(作习题)

定理7.1 $[B,B](t)=t$

we have write here !!!