高博14讲--第三讲 三维空间刚体运动
旋转矩阵
点和向量、坐标系
刚体是指在运动中和受力作用后,形状和大小不变,而且内部各点的相对位置不变的物体。
- 刚体,不光有位置,还有自身的姿态。
- 相机可以看作三维空间中的刚体,于是,位置是指相机在空间中的哪个地方,而姿态是指相机的朝向。
向量的内积: 对于 a , b ∈ R 3 \ a,b∈R^3 a,b∈R3,内积为: a ⋅ b = a T b = Σ i = 1 3 a i b i = ∣ a ∣ ∣ b ∣ c o s ( a , b ) a·b=a^Tb=\Sigma_{i=1}^3{a_ib_i}=|a||b|cos(a,b) a⋅b=aTb=Σi=13aibi=∣a∣∣b∣cos(a,b)
内积描述了向量间的投影关系。
向量的外积:
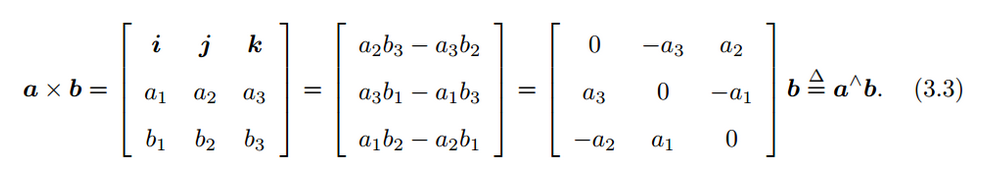 上式中,第一个等号后面为行列式,第三个等号后面的式子,把向量a写成矩阵的形式。
上式中,第一个等号后面为行列式,第三个等号后面的式子,把向量a写成矩阵的形式。
向量的外积,仍是一个向量,外积的方向垂直于这两个向量,大小为 ∣ a ∣ ∣ b ∣ s i n a ( a , b ) \ |a||b|sina(a,b) ∣a∣∣b∣sina(a,b),是两个向量张成的四边形的有向面积。
引入了 ⋀ \ ^{\bigwedge } ⋀ 符号,把 a \ a a 写成一个矩阵, ⋀ \ ^{\bigwedge } ⋀ 是反对称符号, a ⋀ \ a^{\bigwedge } a⋀ 是一个3×3反对称矩阵。 向量 b \ b b 是3×1的矩阵,所以,它们可以写成相乘的形式。即:
把向量的外积 a × b \ a{\times }b a×b写成矩阵与向量的乘法 a ⋀ b \ a^{\bigwedge }b a⋀b。
外积只对三维向量存在定义,用外积表示向量的旋转。
为什么外积可以表示旋转呢?
两个不平行的向量 a , b \ a,b a,b,从 a \ a a到 b \ b b如何进行旋转,在右手法则下,用右手的4个指头从 a \ a a转向 b \ b b,大拇指朝向就是旋转向量的方向,事实上也是 a × b \ a×b a×b的方向。 通过这种方式,构造了从 a \ a a到 b \ b b的一个旋转向量。
所以, a × b \ a×b a×b这个外积可以表示向量从 a \ a a到 b \ b b的旋转。

坐标系间的欧式变换
坐标系之间的变换由一个旋转和一个平移两部分组成。
欧式变换: 同一个向量在各个坐标系下的长度和夹角都不会发生变化的变换。
设某个单位正交基
(
e
1
,
e
2
,
e
3
)
\ (e_1,e_2,e_3)
(e1,e2,e3)经过一次旋转,变成了
(
e
1
′
,
e
2
′
,
e
3
′
)
\ (e_1^{′},e_2^{′},e_3^{′})
(e1′,e2′,e3′)。对于同一个向量
a
\ a
a(注意该向量并没有随着坐标系的旋转而发生运动),它在两个坐标系下的坐标为
[
a
1
,
a
2
,
a
3
]
T
\ [a_1,a_2,a_3]^T
[a1,a2,a3]T 和
[
a
1
′
,
a
2
′
,
a
3
′
]
T
\ [a_1^{′},a_2^{′},a_3^{′}]^T
[a1′,a2′,a3′]T。根据坐标的定义,有:
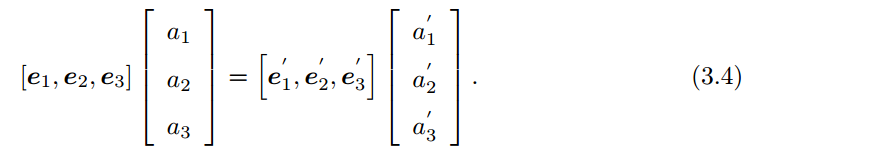
两边同时左乘
[
e
1
T
e
2
T
e
3
T
]
\ \left[ \begin{matrix} e_1^{T} \\ e_2^{T}\\ e_3^{T} \end{matrix} \right]
⎣⎡e1Te2Te3T⎦⎤,左边的系数就变成单位矩阵,所以
 R
\ R
R被称为旋转矩阵:旋转矩阵由两组基之间的内积组成,刻画了旋转前后同一个向量的坐标变换关系。
R
\ R
R被称为旋转矩阵:旋转矩阵由两组基之间的内积组成,刻画了旋转前后同一个向量的坐标变换关系。
旋转矩阵的性质:
- 行列式为1
- 正交阵
- 对于同一个旋转变化,对应唯一的旋转矩阵
- 旋转矩阵的充要条件:行列式为 1 的正交矩阵
- 集合定义:
S
O
(
n
)
=
{
R
∈
R
n
×
n
∣
R
R
T
=
I
,
d
e
t
(
R
)
=
1
}
.
\ SO(n)=\{R∈R^{n×n}|RR^T=I,det(R)=1\}.
SO(n)={R∈Rn×n∣RRT=I,det(R)=1}.
旋转矩阵为正交阵,它的逆(即转置)描述了一个相反的旋转:
 世界坐标系中的向量
a
\ a
a,经过一次旋转和一次平移后,得到
a
′
\ a^{′}
a′,设旋转矩阵为
R
\ R
R,平移向量为
t
\ t
t ,则
世界坐标系中的向量
a
\ a
a,经过一次旋转和一次平移后,得到
a
′
\ a^{′}
a′,设旋转矩阵为
R
\ R
R,平移向量为
t
\ t
t ,则

变换矩阵与齐次坐标
齐次坐标: 射影几何里的概念,把一个三维向量的末尾添加 1,变成了四维向量,称为齐次坐标。
变换矩阵
T
\ T
T:4 × 4矩阵,左上角是 3 × 3 旋转矩阵
R
\ R
R,下面是3 × 1零向量,右面是1 × 3平移向量
t
\ t
t ,右下角是1。
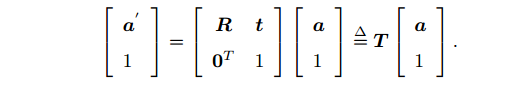
在齐次坐标中,某个点
x
\ x
x 的每个分量同乘一个非零常数
k
\ k
k 后,仍然表示的是同一个点。
因此,一个点的具体坐标值不是唯一的。 当最后一项不为零时,我们总可以把所有坐标除以最后一项,强制最后一项为 1,从而得到一个点唯一的坐标表示。忽略掉最后一项,这个点的坐标和欧氏空间就是一样:
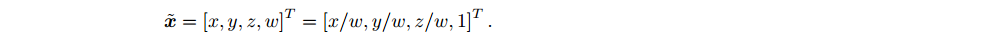 依靠齐次坐标和变换矩阵,两次变换的累加就可以有很好的形式:
依靠齐次坐标和变换矩阵,两次变换的累加就可以有很好的形式:
 变换矩阵
T
\ T
T具有特别的结果:左上角为旋转矩阵,右侧为平移向量,左下角为 0 向量,右下角为 1。这种矩阵又称为特殊欧式群。
变换矩阵
T
\ T
T具有特别的结果:左上角为旋转矩阵,右侧为平移向量,左下角为 0 向量,右下角为 1。这种矩阵又称为特殊欧式群。
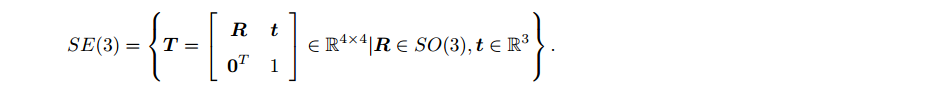
变换矩阵的逆,表示反向变换:
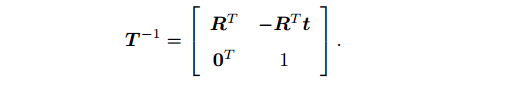
旋转向量和欧拉角
旋转向量
矩阵表示的缺点: 旋转矩阵有9个量,但只有3个自由度;变换矩阵由16个量,但只有6个自由度,表达冗余,浪费空间。
任意旋转都可以用一个旋转轴和一个旋转角来刻画。
旋转向量(或轴角): 方向与旋转轴一致,长度等于旋转角的向量。
旋转向量有3个量和3个自由度,使用一个旋转向量和一个平移向量即可表达一次变换。
旋转向量和旋转矩阵的转换:
1. 旋转向量==>旋转矩阵:罗德里格斯公式
设旋转轴向量(单位向量)
n
\ n
n ,旋转角为
θ
\ θ
θ ,则旋转向量为
θ
n
\ θn
θn,罗德里格斯公式如下:
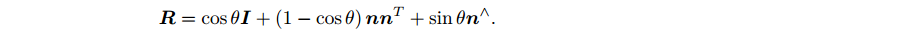 2. 旋转矩阵==>旋转向量,公式如下:
2. 旋转矩阵==>旋转向量,公式如下:

转轴
n
\ n
n 是矩阵
R
\ R
R 特征值 1 对应的特征向量,旋转轴经过旋转之后不变。
欧拉角
欧拉角使用了三个分离的转角,把一个旋转分解成三次绕不同轴的旋转。
欧拉角常使用“偏航-俯仰-滚转”(yaw-pitch-roll),等价于
Z
Y
X
\ ZYX
ZYX 轴的旋转。使用
[
r
,
p
,
y
]
T
\ [r,p,y]^T
[r,p,y]T 这样一个三维的向量描述任意旋转,注意是先
y
\ y
y,再
p
\ p
p,再
r
\ r
r 。
欧拉角的万向锁问题:在俯仰角为
±
9
0
◦
\ ±90^◦
±90◦时,第一次旋转与第三次旋转将使用同一个轴,使得系统丢失了一个自由度(由三次旋转变成了两次旋转),也被称为奇异性问题。
欧拉角的万向锁就是指,有两种方式可以到达相同的旋转效果。一种是绕三个轴各旋转一次,另一种就是绕两个轴各旋转一次,都能从相同的初始姿态到达,最后相同的姿态。
在旋转过程中,数据会有误差存在,比如测定的旋转为
9
0
◦
\ 90^◦
90◦,而实际旋转了
9
1
◦
\ 91^◦
91◦.
这里的旋转是按自身本体的坐标系进行旋转,即:当旋转体本身在旋转时,按照自身来建立坐标系,根据自身坐标系的 x \ x x轴(或 y \ y y轴,或 z \ z z轴)进行一次旋转,在旋转之后,再按照当前位置,自身坐标系绕的 y \ y y轴(或 z \ z z轴,或 y \ y y轴)进行一次旋转,在旋转之后,再按照当前位置,自身坐标系绕的 z \ z z轴(或 x \ x x轴,或 x \ x x轴)进行一次旋转。
理论上可以证明,只要我们想用三个实数来表达三维旋转时,都会不可避免地碰到奇异性问题。
由于奇异性问题,欧拉角不适于插值和迭代,往往只用于人机交互中,也很少出现在slam中。

四元数
四元数的定义
没有不带奇异性的三维向量描述方式(旋转向量、欧拉角……)
四元数是扩展的复数,由一个实部和三个虚部构成,它是紧凑的,没有歧义性
 虚部满足如下关系式:
虚部满足如下关系式:
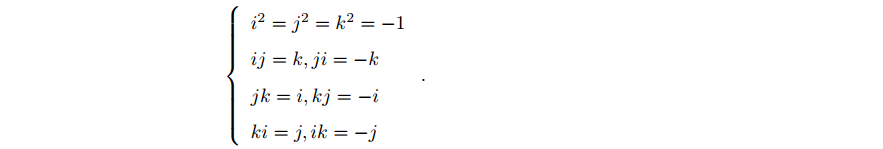
四元数还可以表示成如下表达式:
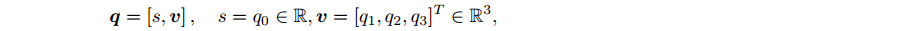 s
\ s
s 称为四元数的实部,而
v
\ v
v 称为它的虚部。如果一个四元数虚部为 0,称之为实四元数。反之,若它的实部为 0,称之为虚四元数。
s
\ s
s 称为四元数的实部,而
v
\ v
v 称为它的虚部。如果一个四元数虚部为 0,称之为实四元数。反之,若它的实部为 0,称之为虚四元数。
用单位四元数表示三维空间中任意一个旋转。设某个旋转是绕单位向量
n
=
[
n
x
,
n
y
,
n
z
]
T
\ n=[nx,ny,nz]^T
n=[nx,ny,nz]T进行了角度为
θ
\ θ
θ 的旋转,那么这个旋转的四元数形式为:
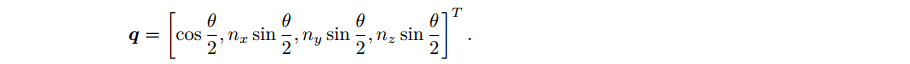 θ
\ θ
θ 加上
2
π
\ 2π
2π,得到一个相同的旋转,但此时对应的四元数变成了
−
q
\ -q
−q。
θ
\ θ
θ 加上
2
π
\ 2π
2π,得到一个相同的旋转,但此时对应的四元数变成了
−
q
\ -q
−q。
在四元数中, 任意的旋转都可以由两个互为相反数的四元数表示。
取
θ
\ θ
θ 为
0
\ 0
0,则得到一个没有任何旋转的实四元数:
q
0
=
[
±
1
,
0
,
0
,
0
]
T
q_0=[\pm1,0,0,0]^T
q0=[±1,0,0,0]T
四元数的运算
四元数和负数一样,可进行一系列运算,如:四则运算、数乘、求逆、共轭。
设两个四元数为
q
a
,
q
b
\ q_a,q_b
qa,qb,它们的向量表示为
[
s
a
,
v
a
]
,
[
s
b
,
v
b
]
\ [s_a,v_a],[s_b,v_b]
[sa,va],[sb,vb],或原始四元数表示为:
q
a
=
s
a
+
x
a
i
+
y
a
j
+
z
a
k
,
q
b
=
s
b
+
x
b
i
+
y
b
j
+
z
b
k
q_a=s_a+x_ai+y_aj+z_ak,q_b=s_b+x_bi+y_bj+z_bk
qa=sa+xai+yaj+zak,qb=sb+xbi+ybj+zbk
- 加减法:

- 乘法:把 q a \ q_a qa的每一项与 q b \ q_b qb相乘,最后相加,按照实部和虚部分别整理
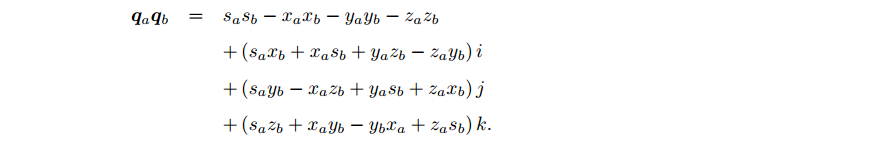
用向量和内外积形式表示:
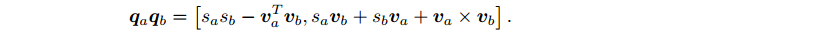
在乘法定义下,两个实数的四元数乘积仍是实的,这与负数也是一致的。
注意四元数乘法是不可交换的,除非
v
a
\ v_a
va 和
v
b
\ v_b
vb 在
R
3
\ R^3
R3 中共线,此时外积项为零。
- 共轭:把虚部取成相反数
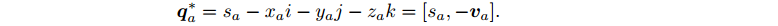
四元数共轭与其本身相乘,得到一个实四元数,其实部为模长的平方:
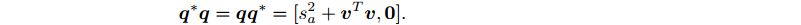
- 模长 :各个部系数平方和开根号
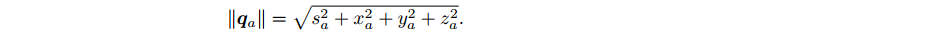 两个四元数乘积的模等于模的乘积,对于单位四元数,则意味着单位四元数乘积仍为单位四元数:
两个四元数乘积的模等于模的乘积,对于单位四元数,则意味着单位四元数乘积仍为单位四元数:

- 逆:

四元数和自己的逆的乘积为实四元数 1 \ 1 1:
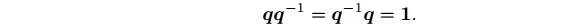
如果 q \ q q为单位四元数,其逆和共轭就是同一个量。
乘积取逆等于交换顺序取逆的乘积:
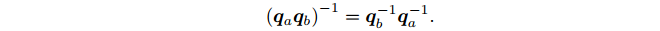
- 数乘和点乘:
与向量相似,四元数可以与数相乘:
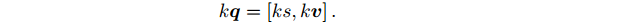
点乘是指,两个四元数每个位置上的数值分别相乘:
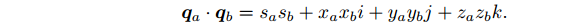
用四元数表示旋转
假设一个三维空间的点
p
=
[
x
,
y
,
z
]
∈
R
3
\ p=[x,y,z]∈R^3
p=[x,y,z]∈R3,以及一个由轴角
n
,
θ
\ n,θ
n,θ指定的旋转。三维点
p
\ p
p经过旋转之后变成
p
′
\ p^{′}
p′
用矩阵描述,则有
p
′
=
R
p
\ p^{′}=Rp
p′=Rp
把这个三维空间的点用虚四元数描述:
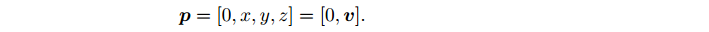
相当于把四元数的3个虚部与空间中的3个轴相对应。
用四元数
q
\ q
q表示这个旋转:

则旋转后的向量为:
p
′
=
q
p
q
−
1
\ p^′=qpq^{−1}
p′=qpq−1
计算结果的实部仍然为0,故为纯虚四元数。其虚部的3个分量表示旋转后
3
D
\ 3D
3D点的坐标。
四元数到旋转矩阵的转换
四元数==>旋转矩阵: 设四元数
q
=
q
0
+
q
1
i
+
q
2
j
+
q
3
k
\ q=q_0+q_1i+q_2j+q_3k
q=q0+q1i+q2j+q3k ,对应的旋转矩阵为:
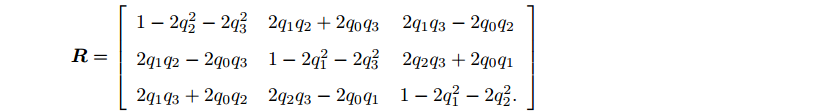
旋转矩阵==>四元数: 设矩阵为
R
=
m
i
j
,
i
,
j
∈
[
1
,
2
,
3
]
\ R={m_{ij}},i,j∈[1,2,3]
R=mij,i,j∈[1,2,3],则对应的四元数为:
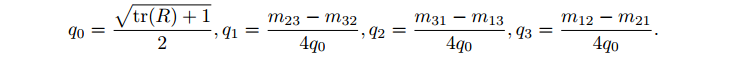
由于
q
\ q
q和
−
q
\ -q
−q表示同一个旋转,一个
R
\ R
R 对应的四元数表示并不唯一。
相似、仿射、射影变换

- (a)相似变换: 圆被影像为圆,方砖被影像为正方形。形状不变,只改变了图像的大小。
- (b)仿射变换: 圆被影像为椭圆,方砖被影像为平行四边形。平行不变性,在仿射变换之后,虽然原来的图形变样了,但原来平行的直线,仍然是平行的。
- (c)射影变换: 平行世界的线被影像为聚线。近大远小,离摄像机近的方砖的图像比远的大。直线不变性,射影变换之后,原来的直线,仍然还是直线。
相似变换
相似变换比欧氏变换多了一个自由度,它允许物体进行均匀的缩放,其矩阵如下:

s
\ s
s称为缩放因子,表示在对向量旋转之后,可以在
x
,
y
,
z
\ x,y,z
x,y,z 三个坐标上进行均匀的缩放。
由于含有缩放,相似变换后不再保持图形的面积不变。
仿射变换
仿射变换也称正交投影,变换矩阵如下:

仿射变换只要求 A 是一个可逆矩阵,而不必是正交矩阵。
经过仿射变换之后,立方体就不再是方的了,但是各个面仍然是平行四边形。
射影变换
摄影变换是最一般的变换,变换矩阵为:

左上角为可逆矩阵
A
\ A
A,右上角为平移
t
\ t
t ,左下角为缩放$ a^T$。
采用齐次坐标,当
v
\ v
v≠0 时,对整个矩阵除以
v
\ v
v 得到一个右下角为1的矩阵,否则得到右下角为0的矩阵。
2
D
\ 2D
2D 的射影变换一共有 8 个自由度,
3
D
\ 3D
3D 则共有 15 个自由度。

参考:https://blog.csdn.net/weixin_40883049/article/details/86567439#311__3
https://blog.csdn.net/qq_35604674/article/details/88606959
























 2488
2488











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








