【Unity编程】四元数(Quaternion)与欧拉角

欧拉旋转、四元数、矩阵旋转之间的差异

除了欧拉旋转以外，还有两种表示旋转的方式：矩阵旋转和四元数旋转。接下来我们比较它们的优缺点。

---

欧拉角

• 优点：三个角度组成，直观，容易理解。
• 优点：可以进行从一个方向到另一个方向旋转大于180度的角度。
• 弱点：死锁问题。 前面《【Unity编程】欧拉角与万向节死锁（图文版）》已经介绍过万向节死锁问题。

四元数

内部由四个数字（在Unity中称为x，y，z和w）组成，然而这些数字不表示角度或轴，并且通常不需要直接访问它们。除非你特别有兴趣深入了解四元数学，你只需要知道四元数表示三维空间中的旋转，你通常不需要知道或修改x，y和z属性。

• 优点：四元旋转不存在万向节锁问题。
• 优点：存储空间小，计算效率高。
• 弱点：单个四元数不能表示在任何方向上超过180度的旋转。
• 弱点：四元数的数字表示不直观。

矩阵旋转

• 优点：与四元数一样，不存在万向节锁问题
• 优点：可以表示围绕任意轴的旋转，四元数的旋转轴均为通过物体中心点的轴，矩阵则不受限
• 缺点：矩阵旋转使用4x4矩阵，记录16个数值，而四元数只需要4个数值。计算复杂，效率低。
  

  ---

由于Unity中的旋转使用四元数，因此本文重点就放在四元数数学上。矩阵还是某些场合需要用到，比如坐标变换。不过你几乎不需要手动去执行矩阵计算，除非你在做Shader编程，或者是某些需要极端提高效率的场合。后续我计划写一篇文章专门介绍矩阵变换。

四元数的数学

由于前面两篇文章均尽可能采用无数字计算的方式，为的是方便理解。而这里由于需要理解四元数的计算，我们还是需要理解一些复数和欧拉旋转计算方面的基本数学。

复数

首先了解一下复数，上图中，左右方向的轴（X轴）称为实数轴，上下的轴(Y轴)称为虚数轴。
任意一个二维矢量，都可以使用一个复数形式进行表示。也就是：e = a + bi
其中a是实数，i是虚数，i * i=-1。

至于什么是虚数，我的理解它就是个不同维度的后缀标记和符号而已。i标记了实数轴和虚数轴之间的差异，也就是旋转90度旋转的差别，乘以i意味着这种旋转关系。
为什么i * i=-1?也就是两个虚数i乘积又变成了实数-1？因为从实数轴(1表示)围绕上图中逆时针90度(1*i)到达虚数轴(=i)，再逆时针旋转90(1 * i * i)就到达了负实数轴方向(=-1)。所以这里规定i * i=-1。

复数运算

• 加法： (a+bi)+(c+di)=(a+c)+(b+d)i
• 减法： (a+bi)-(c+di)=(a-c)+(b-d)i
• 乘法： (a+bi)(c+di)=ac+bci+adi+bdi^{2}=(ac-bd)+(bc+ad)i

更多复数相关知识，请参考“维基百科-复数_(数学)”

欧拉旋转定理

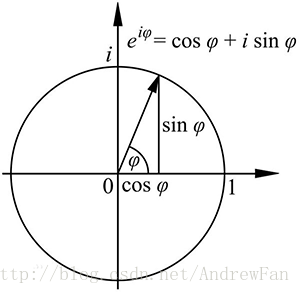
为了方便讨论旋转，我们避开矢量长度的影响，也就是假设问题是基于长度为1的矢量去讨论。由上图可以看出，当长度为1时，矢量落在长度为1的圆形上，此时实数轴上的a = cos（φ），虚数轴上的b = sin（φ），其中φ为旋转角度。

此时的表示形式为 e = cos（φ） + sin（φ）i

那么，使用这样一种形式到底有什么意义呢？数学从来都是工具，如果没有用处，它也就不会存在了。我们接下来看它的作用。

当圆上的一个矢量进行了连续的旋转时时，假设先旋转φ，再旋转θ，则结果应该是两个旋转的角的和的复数形式，即 e = cos（φ+θ）+sin（φ+θ）i

假设：
e1= cos（φ） + sin（φ）i (表示旋转了φ角度)
e2= cos（θ） + sin（θ）i (表示旋转了θ角度)

那么e和e1、e2之间的关系是怎样的？

---

根据和差公式可以得知

cos（φ+θ）+sin（φ+θ）i
= （cos（φ）cos（θ）-sin（φ）sin（θ））+(sin（θ）cos（φ）+cos（θ）sin（φ）)i
= cos（φ）cos（θ）+cos（φ）sin（θ）i+cos（θ）sin（φ）i- sin（φ）sin（θ）
= (cos（φ） + sin（φ）i)*(cos（θ） + sin（θ）i)
= e1 * e2

=>

e = e1*e2

---

也就是说，连续的旋转（例如这里旋转φ再旋转θ），可以使用两个复数的乘积进行表示。在计算机运算中：

• 如果知道φ=30度，那么计算此单位矢量再旋转θ=40度是很容易的，只需要直接运算cos（φ+θ）和sin（φ+θ）即可。
• 如果知道一个矢量(a+bi)，不知其φ值，要对其进行旋转θ=40度，那么也就有了快速的计算方法，即：
  (a+bi) * (cos(40)+sin(40)i) = (a * cos(40)-b * sin(40)) + (b * cos(40) + a * sin(40))i
  结果：二维向量 x = a * cos(40)-b * sin(40)，y= b * cos(40) + a * sin(40)
  可以快速计算出二维矢量结果，而不必先求φ。

因此这就是复数和欧拉旋转定理的作用，它可以使用复数很方便地表示出二维矢量的旋转变化。

四元数

相对于复数为二维空间，为了解决三维空间的旋转变化问题，爱尔兰数学家威廉·卢云·哈密顿把复数进行了推广，也就是四元数。

以下均为定义，所谓定义，就是我们人为设置的概念和计算方法，它们本身或许没有什么意义，但是如果按照这些概念和方法计算出某些有意义的结果，那么这些定义也就有了相应的意义。

---

四元数定义

四元数定义i、j、k三个虚数单位参与运算，并有以下运算规则：

$$j*k= i , k*j = -i;$$ $$j*k= i , k*j = -i;$$ $$k*i= j , i*k = -j;$$ $$i*i= j*j = k*k = i*j*k =-1$$

i、j、k仍然理解为旋转，其中：

• i旋转代表X轴与Y轴相交平面中X轴正向向Y轴正向的旋转
• j旋转代表Z轴与X轴相交平面中Z轴正向向X轴正向的旋转
• k旋转代表Y轴与Z轴相交平面中Y轴正向向Z轴正向的旋转
• -i、-j、-k分别代表i、j、k旋转的反向旋转

一个普通四元数可以写成如下形式：

$$\overline q=a+bi+cj+dk$$

四元数的i、j、k之间乘法的性质与向量之间的叉积结果形式很类似，于是四元数有了另外一种表示形式：

$$\overline q=(\vec{（x,y,z）},w)=(\vec u,w)$$

加法定义

四元数加法，跟复数、矢量和矩阵一样，两个四元数之和需要将不同的元素加起来，加法遵循实数和复数的所有交换律和结合律：

$${\displaystyle \overline q_1+\overline q_2=w_1+w_2+{\vec {u_1}}+{\vec {u_2}}=(w_1+w_2)+(x_1+x_2)i+(y_1+y_2)j+(z_1+z_2)k}$$

格拉斯曼积定义

四元数的乘法有很多种，最常见的一种定义，与数学多项式乘法相同，称为格拉斯曼积。(注意，下面乘积的式子是由多项式形如a+bi+cj+dk的多项式进行多对多乘法(比如4项x4项=16项)计算后，使用矢量的点积和叉积替代部分计算项后形成)：

$$\overline q_1\overline q_2=w_1w_2-{\vec {u_1}}\cdot {\vec {u_2}}+w_1{\vec {u_2}}+w_2{\vec {u_1}}+{\vec {u_1}}\times {\vec {u_2}}$$

把向量部分和实数部分分开，可以写成：

$$\overline q_1\overline q_2=((w_1{\vec {u_2}}+w_2{\vec {u_1}}+{\vec {u_1}}\times {\vec {u_2}}),(w_1w_2-{\vec {u_1}}\cdot {\vec {u_2}}))$$ 注意，格拉斯曼积符合结合率，也就是 $\overline q_1\overline q_2\overline q_3=(\overline q_1\overline q_2)\overline q_3=\overline q_1(\overline q_2\overline q_3)$，但不符合交换律，一般来说， $\overline q_1\overline q_2≠\overline q_2\overline q_1$。

点积定义

点积也叫做欧几里得内积，四元数的点积等同于一个四维矢量的点积。点积的值是 $\overline q_1$中每个元素的数值与 $\overline q_2$ 中相应元素的数值的一对一乘积(比如4项x4项=4项)的和。这是四元数之间的可换积，并返回一个标量。

q¯1⋅q¯2=w1w2+u1→⋅u2→=w1w2+x1x2+