MVG读书笔记——射影几何下的二次曲线

最新推荐文章于 2023-05-31 11:46:07 发布

炽霜

最新推荐文章于 2023-05-31 11:46:07 发布

阅读量5.8k

点赞数 4

分类专栏：几何基础文章标签：读书笔记 MVG

本文链接：https://blog.csdn.net/frozenspring/article/details/76522264

版权

几何基础专栏收录该内容

17 篇文章

订阅专栏

本文详细介绍了二次曲线的概念，包括双曲线、椭圆和抛物线等，并探讨了它们在齐次坐标下的表示方法及矩阵形式。此外，还讲解了二次曲线的切线、极线和退化情况，并引入了对偶二次曲线的概念。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

双曲线、椭圆、抛物线等统称为二次曲线（或圆锥曲线），它其实是三维空间中圆锥在截面上的投影，如图

在这里插入图片描述

齐次坐标下的二次曲线表示

二次曲线的在欧氏空间的方程为
$ax^2+bxy+cy^2+dx+ey+f=0$
即一个二次多项式。

使用齐次坐标表示为
$ax_1^2+bx_1x_2+cx_2^2+dx_1x_3+ex_2x_3+fx_3^2=0$
使用矩阵形式表示为 $x^TCx=0$
其中 $C=\begin{bmatrix}a&b/2&d/2\\b/2&c&e/2\\d/2&e/2&f\end{bmatrix}$
显然，一个二次曲线有5个自由度，5点确定一条二次曲线。

二次曲线的切线

二次曲线在其上一点x处的切线为 $l = C x$

极线

平面上任意一点和二次曲线可以定义一条直线 $l = C x$ ，这条直线称为x之于C的极线。x称为l之于C的极点。如图,
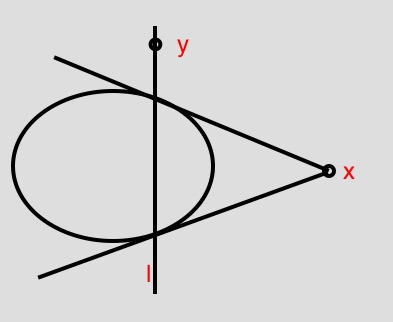
polar

过x作C的切线刚好落在极线上。

极线上满足 $y^TCx=0$ 的点y称为x之于C的共轭点。相应的，x也在y之于C的极线上。

退化

可以看到二次曲线的矩阵表示实际上是一个二次型，当C不是满秩的时候，二次曲线发生退化。此时二次曲线的形状可能为两条（秩为2）或一条直线（秩为1）

一个退化为两条直线的二次曲线方程为 $C = lm^T+ml^T$ 。证明如下：

对l上的一点x，它满足 $x^TCx=(x^Tl)(m^Tx)+(x^Tm)(l^Tx)=0$ 。故x在曲线C上。
##对偶二次曲线
之前讲到射影几何中点与直线具有对偶性。由此我们可以定义出二次曲线（或者叫点二次曲线）的对偶曲线，称为线二次曲线。正如点二次曲线是无数点的集合，线二次曲线是无数线的集合

我们还是可以用一个 $3\times 3$ 的对称矩阵来 $C^*$ 来表示它。 $C^*$ 为C的伴随矩阵。与线二次曲线相切的直线满足 $l^TC^*l=0$ 。在满秩的情况下有 $C^*=kC^{-1}$

线二次曲线可以很简单的由点二次曲线推导出来。由上面所说，点二次曲线C在x处点切线为l=Cx。相反的，我们可以得到C与直线l相切于 $x=C^{-1}l$ 。于是由 $x^TCx=0$ 我们得到 $C^{-1}l)^TC(C^{-1}l)=l^TC^{-1}l=0$ 。即线二次曲线的方程。
dual conic
如图为一个对偶二次曲线的直观表示。它包住了点圆锥曲线所在的区域。