三大变换与自控（九）二阶动态系统的建模与分析

前面介绍了一阶动态系统和极点的概念，现在来看看二阶系统。

首先我们还是举个二阶动态系统的例子。比如说运动。

根据牛顿定理，物体运动的外力F = ma， 而加速度实际上是物体位置的二阶导，因此物体运动实际上是一个二阶微分方程，也就是二阶动态系统。

再举一个详细点的例子，弹簧。当你把弹簧拉直后松开，弹簧是不是回缩回去，然后弹回来，循环往复直至平息？

这个弹簧的运动轨迹看起来像不像一个一维空间上的三角函数？那么究竟是不是呢，我们可以用弹簧为例来进行数学建模和分析。

首先，我们根据物理定理进行受力分析，并列出我们的微分方程：
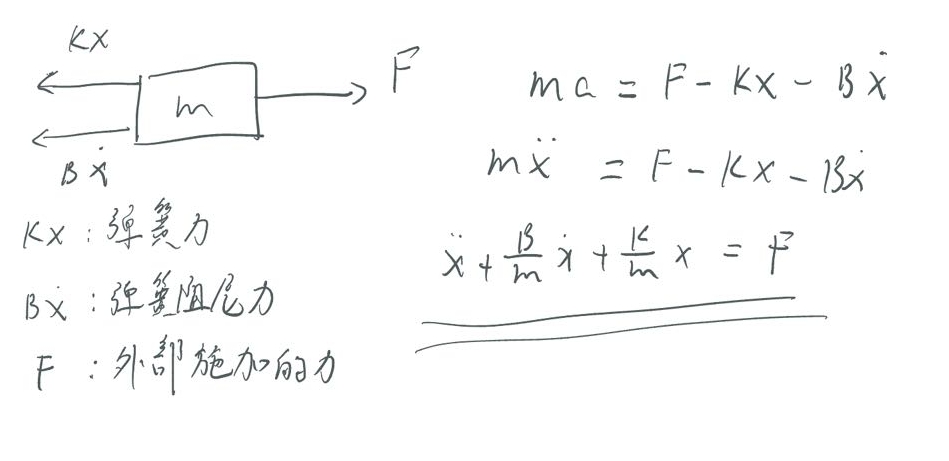这个时候，我们进行一个非常重要的定义：

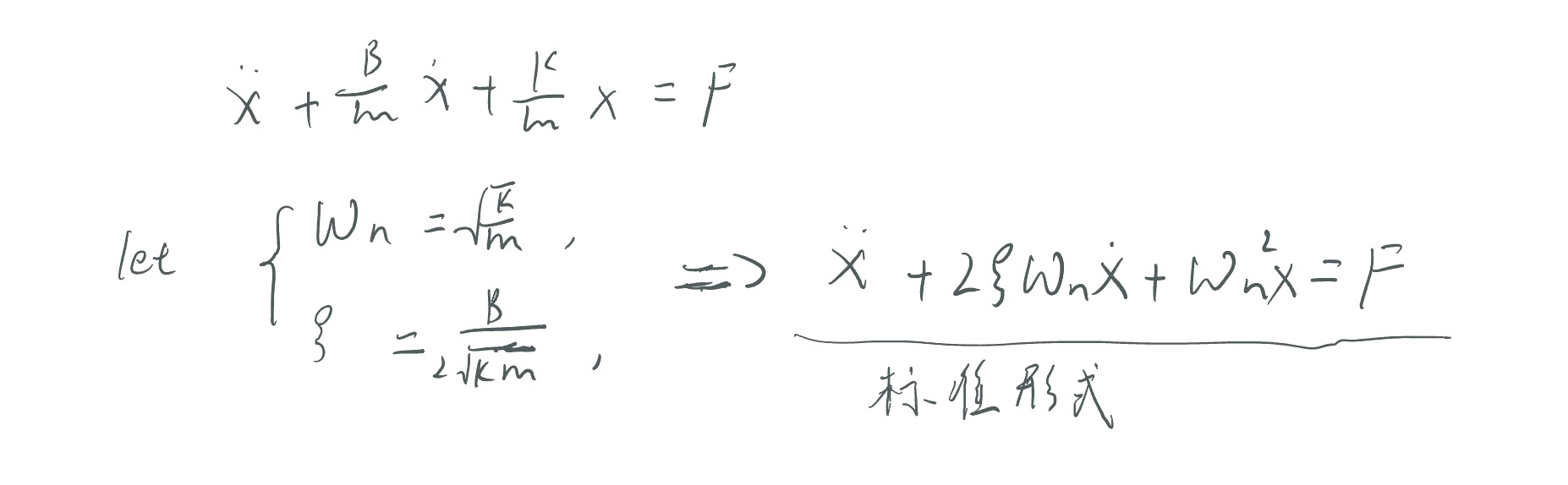
为什么要这样定义呢？原因很简单，变换后这样的形式被称为二阶系统的标准形式，其中参数ζ和Wn直接决定了系统的响应和性能，在后续的数学推导中我们可以轻易看出这一点。

其中ζ被称为阻尼比（damping ratio），Wn被称为固有频率（natural frequency）。

下面来求解标准形式二阶微分方程，先令F=0，即没有外部输入的情况。

二阶微分方程的解为：
x(t) = e^(λt)
x’(t) = e^(λt)
x’'(t) = e^(λt)

怎么解出来的我们先略过，放在后面来证明，我们先关注系统本身。

把解带入方程：

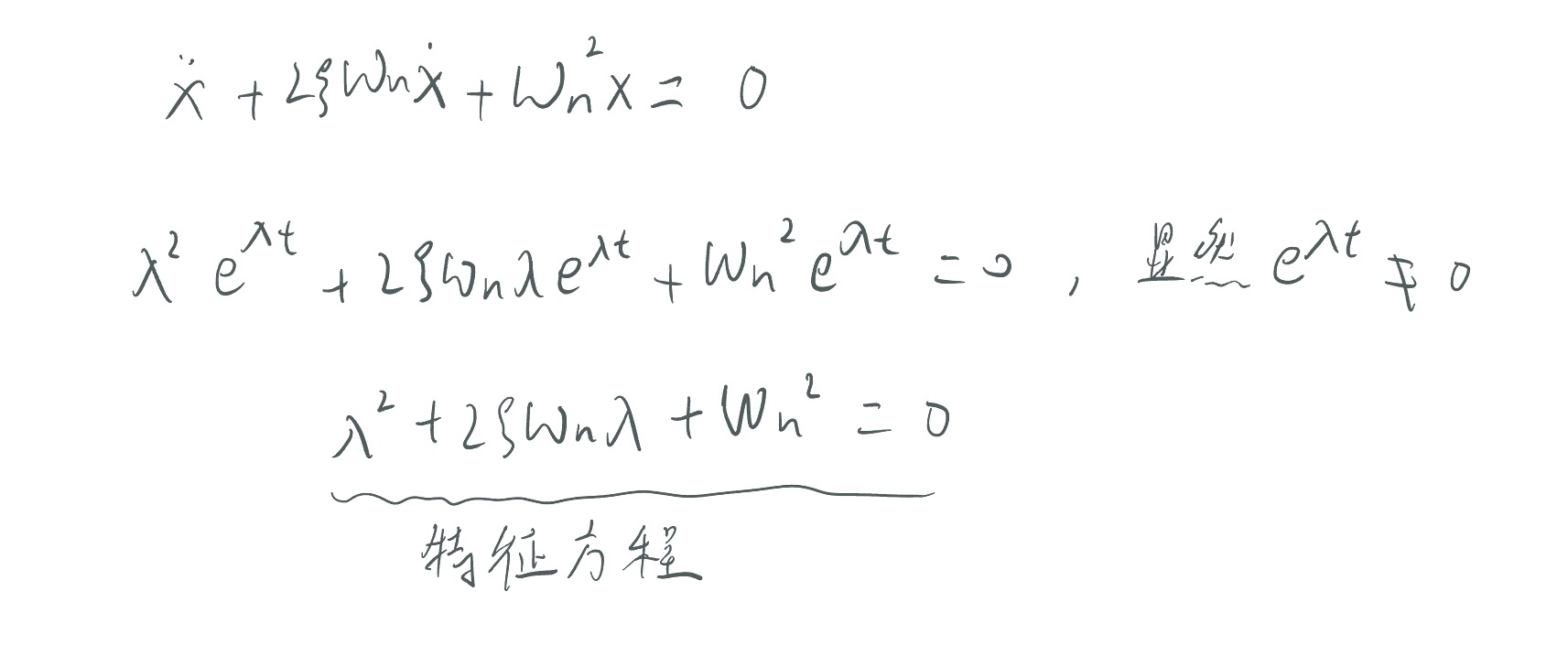
化简得到的这个二元一次方程就叫做特征方程（characteristic equation）。

为什么要单独给它命名呢，因为这个特征方程的解λ就是二阶微分方程的解的唯一未知参数，也就是说，解出这个特征方程，就等于解出了二阶微分方程，等于我们彻底掌握了二阶动态系统。

解一元二次方程用求根公式即可：
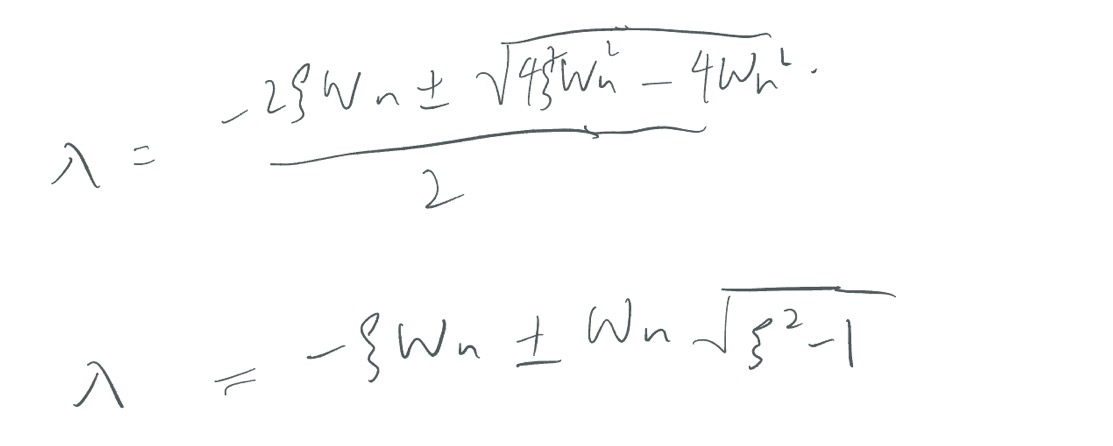显然，不同的ζ值导致的结果也有很大的区别。

当ζ大于1时，λ的值为两个负实数，此时二阶系统的解为：
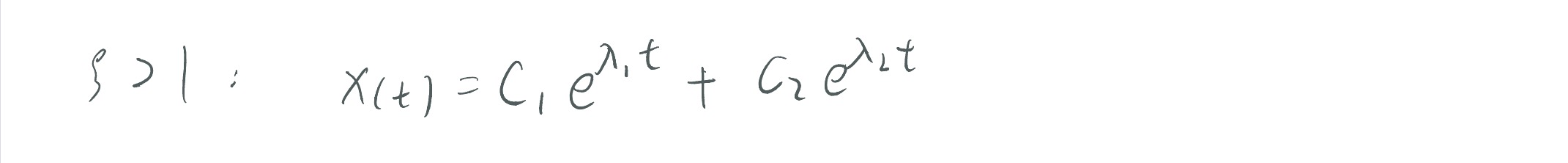输出由两个指数函数构成，一个收敛快一个收敛慢，因此系统收敛速度主要由收敛慢的那个决定。

而C1和C2的值则由X(0)和X’(0)的值决定。

什么意思呢，还是拿弹簧为例，λ代表了二阶微分方程的通解，即弹簧本身。但是弹簧具体如何运动则是包含在通解内的一个特解。

例如，我把弹簧拉长一厘米后松开，这和我把弹簧拉长两厘米后松开后的运动轨迹肯定是不同的。

一个X(0)为1cm，一个X(0)为2cm，显然后者的C1和C2值更大，也就是说弹簧振幅更大。

再比如我猛地击打弹簧，初始时刻弹簧的位置X(0)虽然还是0，但X’(0)不为0，弹簧自然会运动起来。若X(0)和X’(0)都是0，又没有外部施加的力，显然弹簧不会动，带入公式发现X(t)=0，也是符合理论的。

言归正传，我们把ζ>1的情况叫做过阻尼（over damped），此时系统输出类似这样：

实际就是两个一阶系统相加，最终表现形式也非常相似。

第二种情况是ζ刚好等于1时，此时λ只有一个解，和一阶系统等价，我们称之为临界阻尼（critical damped）。

第三种是最普遍的情况，即0<ζ<1，这时λ的解为共轭的两个复数，且实数部分依然小于零。弹簧就是一个典型的欠阻尼系统。

这种情况我们称之为欠阻尼（under damped）。

此时方程的通解为：
果然和我们猜测的一样，弹簧的运动轨迹就是一个三角函数。

在推导过程中我们令Wd=Wn（1-ζ²)^-2，这个Wd被称作阻尼固有频率（damped natural frequency），注意观察，Wd，ζ，Wn是满足直角三角形关系的，感兴趣的可以参考我的b站视频《双控制器的并网逆变器设计，plecs仿真》17分30秒。

欠阻尼系统的输出由两部分组成，前面指数部分在衰减，乘以一个震荡的三角波，因此系统输出波形类似于这样：

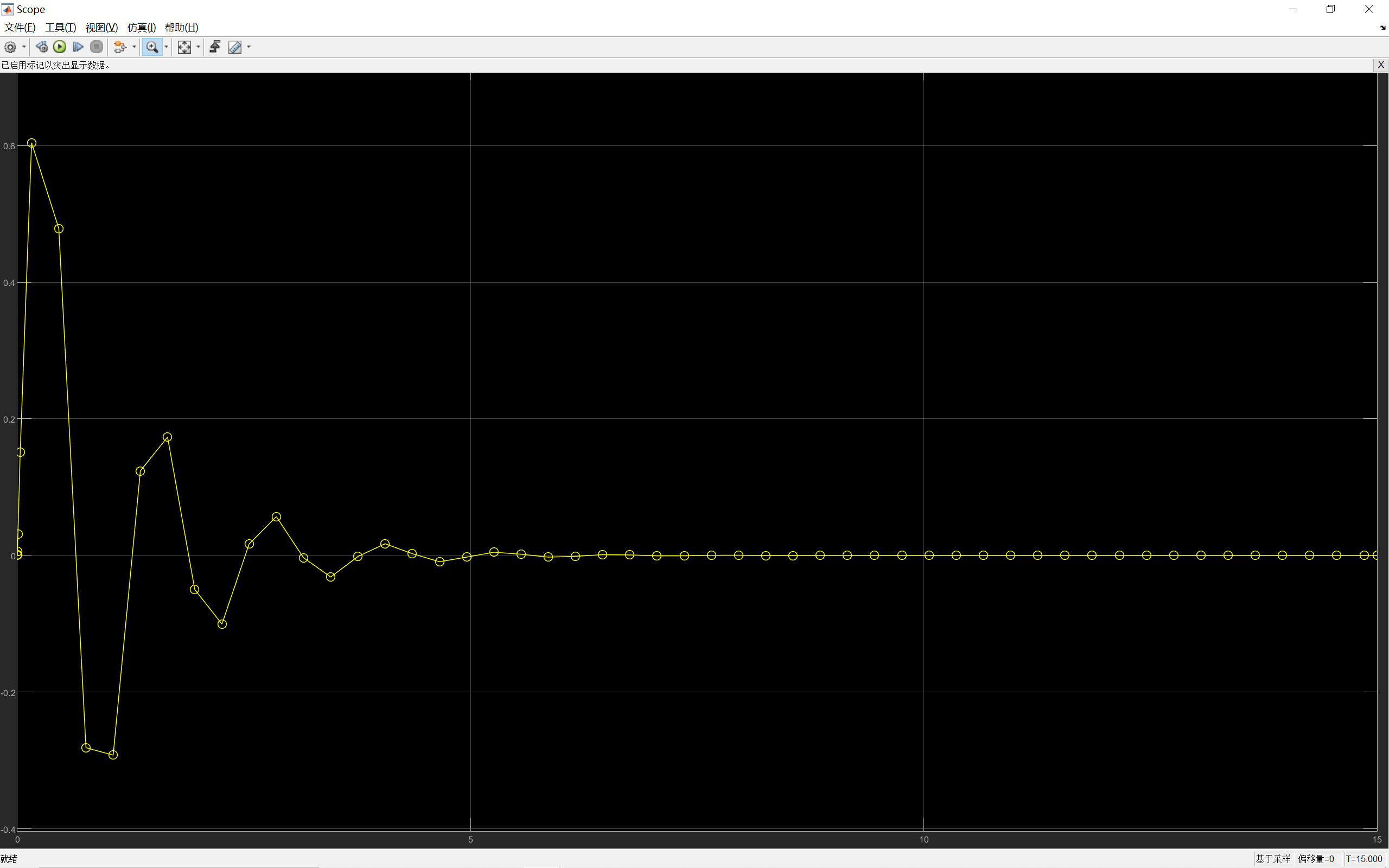震荡的周期为2π/Wd。

第四种是无阻尼系统，即ζ=0，这个时候就没有衰减的指数部分了，系统会永远震荡下去。

第五，六种情况分别是-1<ζ<0，ζ<-1。

这两种情况下λ的实数部分不为负数，也就是说微分方程的通解的指数部分不是衰减的，而是逐渐增大的，这意味着整个系统并不会趋于收敛，而是会震荡，不稳定：
因此，λ实数部分为负时，系统稳定，实数部分为正时，系统不稳定，这就是我们判断系统稳定性的依据。

好，至此我们的二阶动态系统建模和分析就算完成了。这是自动控制理论最重要的一部分，理解了这个，就理解了自动控制理论的工程方面百分之九十的内容。

文章最后再杂谈一下，作为发散。

这篇文章我们只讨论了初始情况，但加上外部输入也是一样的，因为系统的输出会趋向于输入。比如外部输入为1时，欠阻尼系统的输出是这样的：

因为我们的目的是让系统的输出更快的等于输入，因此从某种意义上来说，其实所谓的控制，就是一个放大器。

我刚上大学的时候就很奇怪，既然我们有参考信号，为什么不直接把参考信号当做输出呢？

这是因为，参考信号往往驱动能力很差。比方说单片机上有一个5v引脚，我们可以直接用它给手机充电吗？显然别说智能手机了，就是诺基亚板砖都费劲。

再比如说自动驾驶，参考信号可能就是计算机里的一个数字，但我们能用这个数字去驱动整辆汽车的运动吗？

因此，我们需要把参考信号进行放大，增强它的驱动能力。

在后续文章中，我们继续讨论一阶二阶系统的阶跃响应和频率响应。

除此之外，正如我们所提到的，当系统的状态改变时或输入改变时，λ的值也在改变（实际就是通解下的多个特解），如果我们把λ变化的值在复平面上画出来，就会形成一条或多条轨迹，这个轨迹也被称为根轨迹。我们设计控制器实际上就是在设计λ的值，以及根轨迹的位置。

只要理解透彻这两篇文章的内容，设计控制器就是手到擒来，顺理成章的事了。