【K8B】鱼眼相机模型

1.【OpenCV】中的鱼眼相机及其标定
2. MATLAB【八】———— matlab 针孔相机模型，建图
3. ORBSLAM3中 src_cameraModels_KannalaBrandt8.cpp 中完成了对于KB模型的代码，介绍一下鱼眼相机以及KB模型。

1. 相机模型概述

鱼眼相机模型主要用于处理广角镜头或鱼眼镜头下的图像畸变，这些镜头具有较大的视角，通常会产生明显的非线性畸变。鱼眼相机模型根据不同的数学建模方法，有多种常见的畸变模型。以下是几种常见的鱼眼相机模型及其详细的梳理和相关公式推导。

2. 鱼眼相机模型分类

主要有以下几种常见的鱼眼相机模型：

• 等距投影模型（Equidistant Projection Model）
• 等立体角模型（Equisolid Angle Projection Model）
• 正交投影模型（Orthographic Projection Model）
• 立体投影模型（Stereographic Projection Model）
• 径向畸变模型（Polynomial or Rational Model, K8B）

3. 各类模型的推导与解释

3.1 等距投影模型（Equidistant Projection Model）

定义：等距投影模型假设图像点与其对应的空间点之间的角度关系是线性的，即图像平面上的径向距离与入射角的大小成正比。

公式推导：

设空间点 $P$ 具有极角 $\theta$ （即相机光轴与入射光线的夹角），图像平面上的径向距离为 $r$，则：

$r=f\cdot \theta$

其中 $f$ 为焦距，$\theta$ 为从光心到空间点的角度。

这个模型简单、计算开销小，适合处理鱼眼镜头具有较大视角的场景，但在某些情况下可能无法很好地描述畸变特性。

3.2 等立体角模型（Equisolid Angle Projection Model）

定义：该模型假设每个像素对应的投影面积在球面上是恒定的，因此适用于较为均匀的畸变分布。

公式推导：

图像平面上的径向距离 $r$ 与入射角 $\theta$ 之间的关系为：

$r=2f\cdot \sin \left(\frac{\theta }{2}\right)$

这个公式能够在大范围角度内提供较好的畸变校正效果，适合使用在均匀视角分布的鱼眼镜头中。

3.3 正交投影模型（Orthographic Projection Model）

定义：正交投影模型是假设入射光线垂直投影到图像平面上，投影过程保持垂直距离。

公式推导：图像平面上的径向距离 $r$ 与入射角 $\theta$ 的关系为：

$r=f\cdot \sin (\theta )$

该模型主要应用在光线入射角不大时，因其在大视角下会产生较大的误差。

3.4 立体投影模型（Stereographic Projection Model）

定义：立体投影模型假设图像点与空间点的关系符合立体投影规则，适合处理较大视角下的畸变校正问题。

公式推导：

图像平面上的径向距离 $r$ 与入射角 $\theta$ 之间的关系为：
$r=2f\cdot \tan \left(\frac{\theta }{2}\right)$

这种模型较为精确，尤其适合鱼眼镜头的畸变校正，但计算复杂度相对较高。

3.5 径向畸变模型（Polynomial/Rational Model, K8B）

定义：径向畸变模型是广泛应用于图像畸变校正的经典模型。它通过一系列多项式或有理式来表示图像点到畸变中心的径向偏移，主要适用于镜头引起的畸变。

公式推导：

• 径向畸变：
  $$r_{distorted}=r_{ideal}\cdot (1+k_1\cdot r_{ideal}^2+k_2\cdot r_{ideal}^4+k_3\cdot r_{ideal}^6)$$
• 切向畸变： $$u^{\prime }=u+\left(2p_{1}uv+p_2(r^2+2u^2)\right)$$

其中，$k_1,k_2,k_3$ 为径向畸变系数，$r_{ideal}$ 为理想图像点的径向距离，$r_{distorted}$ 为畸变后的图像点的径向距离。

该模型可以通过高阶多项式来拟合不同类型的畸变。实际应用中，常用的模型为五参数模型（即 $k_1,k_2,k_3,p_1,p_2$，其中 $p_1,p_2$ 控制切向畸变）。

K8B模型 是径向畸变模型的扩展形式，其中通过引入高阶系数来处理复杂畸变。

4. 鱼眼相机模型的比较

• 等距投影模型：简单高效，适用于角度较小的鱼眼镜头，较难处理大畸变。
• 等立体角模型：适合处理均匀分布的广角畸变。
• 正交投影模型：应用于较小视角，计算开销小。
• 立体投影模型：精度较高，适合大视角鱼眼镜头。
• 径向畸变模型：最为常用，具有较高的灵活性，能够精确描述各种畸变效果。

4. 非线性优化过程

非线性优化用于精确校正鱼眼镜头畸变，具体流程如下：

1. 建立代价函数：根据不同鱼眼相机模型（如等距、等立体角、径向畸变等），构建代价函数，例如最小化重投影误差。
2. 初始参数估计：给出初始畸变参数（如 ( k_1, k_2, p_1, p_2 ) 等），通过启发式方法或直接测量得到。
3. 优化算法选择：采用Levenberg-Marquardt（LM）算法、Gauss-Newton算法等非线性优化方法对畸变参数进行迭代优化。
4. 迭代更新参数：通过优化过程逐步减小代价函数值，更新畸变参数直至收敛。
5. 最终输出校正结果：得到校正后的图像和畸变模型参数，用于后续图像处理中。

通过这种非线性优化的方式，可以对图像中的畸变进行精确校正。

4.1. 鱼眼相机

鱼眼相机是一种焦距小于等于16mm，且视角接近或者等于180°的极端广角镜头，但是正是因为他极端的短焦和广角，导致它因为光学原理而产生的畸变非常剧烈，所以针孔模型并不能很好的描述鱼眼相机，所以需要一种新的相机模型来对鱼眼相机进行近似模拟。

4.2.1 KB模型

KB模型能够很好的适用于普通，广角以及鱼眼镜头。KB模型假设图像光心到投影点的距离和角度的多项式存在比例关系，角度的定义是点所在的投影光纤和主轴之间的夹角。

KB模型公式：

投影过程

反投影过程

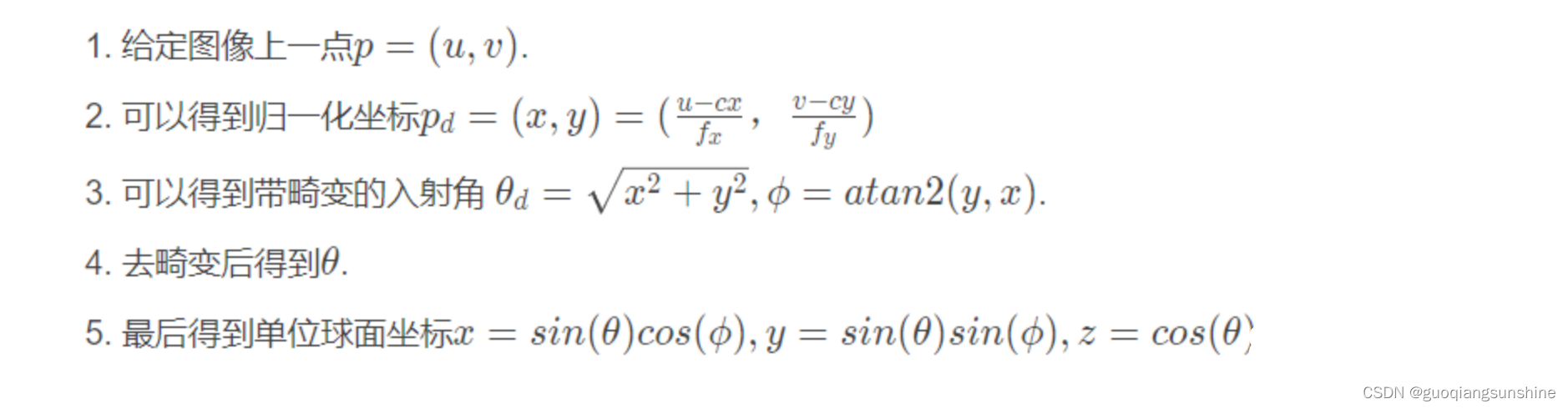
KB算法在ORB-SLAM3实现的KB模型下的投影和反投影关系：（互为逆运算）
1.投影（相机坐标系下3D点 -->图像像素坐标）

/**
  * @brief 投影
  * @param 3D点
  * @return 像素坐标
  * 注意：ORBSLAM3为投影重载了许多方法以接受各种不同的数据类型
 **/
cv::Point2f KannalaBrandt8::project(const cv::Point3f &p3D)
{
	// r^2 = x^2 + y^2
    const float x2_plus_y2 = p3D.x * p3D.x + p3D.y * p3D.y;
    // θ = atan2(r,z) 
    const float theta = atan2f(sqrtf(x2_plus_y2), p3D.z);
    
    const float psi = atan2f(p3D.y, p3D.x);

	// 计算θ的3，5，7，9次方
	// 计算2次方是为了方便计算3，5，7，9次 相当于中间变量
    const float theta2 = theta * theta;
    const float theta3 = theta * theta2;
    const float theta5 = theta3 * theta2;
    const float theta7 = theta5 * theta2;
    const float theta9 = theta7 * theta2;
    // mvParameters是存放相机参数和畸变系数的数组
    // [4] [5] [6] [7] 分别代表k1 k2 k3 k4
    // 是不是感觉很熟悉 其实KB模型也常被用于针孔的畸变模型
    // 计算获得d(θ)
    const float r = theta + mvParameters[4] * theta3 + mvParameters[5] * theta5 + mvParameters[6] * theta7 + mvParameters[7] * theta9;
    // 注意：注释的r和代码的r不是一个东西 代码r = 注释d(θ) 注释r = 代码x2_plus_y2 
	// [0] [1] [2] [3] 分别代表 fx fy cx cy
	// 利用公式 u = (fx * d(θ) * xc) / r 
	// 		    v = (fy * d(θ) * yc) / r
	// cos(psi) = xc/r  sin(psi) = yc/r  
    return cv::Point2f(mvParameters[0] * r * cos(psi) + mvParameters[2],
                        mvParameters[1] * r * sin(psi) + mvParameters[3]);
}

2.反投影（图像像素坐标->相机）

/**
  * @brief 反投影过程
  * @param 像素坐标
  * @return 归一化坐标
  **/
cv::Point3f KannalaBrandt8::unproject(const cv::Point2f &p2D)
{
    //Use Newton method to solve for theta with good precision (err ~ e-6)
    // 使用Newton法来求解θ，获得了很好的效果
    // 获取归一化的x,y坐标
    // x = (u - cx) / fx
    // y = (v - cy) / fy
    cv::Point2f pw((p2D.x - mvParameters[2]) / mvParameters[0], (p2D.y - mvParameters[3]) / mvParameters[1]);  // xd   yd
    // 设置尺度为1
    float scale = 1.f;
    // xd = θd/r * xc   yd = θd/r * yc
    // xd^2 + yd^2 = (θd^2 / r^2) * (xc^2 + yc^2)
    // xc^2 + yc^2 = r^2
    // θ = (xd^2 + yd^2)^(1/2)
    float theta_d = sqrtf(pw.x * pw.x + pw.y * pw.y);  // sin(psi) = yc / r
    //确保θd在[-π,π]的范围内 
    theta_d = fminf(fmaxf(-CV_PI / 2.f, theta_d), CV_PI / 2.f);  // 不能超过180度

	// 已知θd 求解 θ
    if (theta_d > 1e-8)
    {
        //Compensate distortion iteratively
        float theta = theta_d;  // θ的初始值定为了θd
        // 开始迭代
        for (int j = 0; j < 10; j++)
        {
            float theta2 = theta * theta, 
                  theta4 = theta2 * theta2,
                  theta6 = theta4 * theta2,
                  theta8 = theta4 * theta4;
            float k0_theta2 = mvParameters[4] * theta2,
                  k1_theta4 = mvParameters[5] * theta4;
            float k2_theta6 = mvParameters[6] * theta6,
                  k3_theta8 = mvParameters[7] * theta8;
            // f(θ) = θ + k1 * θ^3 + k2 * θ^5 + k3 * θ^7 + k4 * θ^9
            // e(θ) = f(θ) - θd
            // 直接求解θ很难 所以通过求导优化的方法
            // 目标是优化获得e(θ) = 0对应的θ
            // e(θ)' = 1 + 3 * k1 * θ^2 + 5 * k2 * θ^4 + 7 * k3 * θ^6 + 9 * k4 * θ^8
            // δ(θ) = e(θ) / e(θ)' 修正量
            float theta_fix = (theta * (1 + k0_theta2 + k1_theta4 + k2_theta6 + k3_theta8) - theta_d) /
                                (1 + 3 * k0_theta2 + 5 * k1_theta4 + 7 * k2_theta6 + 9 * k3_theta8);
            // 进行修正
            theta = theta - theta_fix;
            // 如果更新量变得很小，表示接近最终值
            if (fabsf(theta_fix) < precision) 
                break;
        }
        //scale = theta - theta_d;
        // 求得tan(θ) / θd
        scale = std::tan(theta) / theta_d;
    }
	// 获取归一化坐标
    return cv::Point3f(pw.x * scale, pw.y * scale, 1.f);
}

3.求解雅各比矩阵

/**
  * @breif 求解像素坐标关于三维点的雅各比矩阵
  * @param p3D 三维点
  * @return 雅各比矩阵[一个两行三列的矩阵] 2*3
  **/
  
cv::Mat KannalaBrandt8::projectJac(const cv::Point3f &p3D)
{
    float x2 = p3D.x * p3D.x, y2 = p3D.y * p3D.y, z2 = p3D.z * p3D.z;
    float r2 = x2 + y2;
    float r = sqrt(r2);
    float r3 = r2 * r;
    float theta = atan2(r, p3D.z);

    float theta2 = theta * theta, theta3 = theta2 * theta;
    float theta4 = theta2 * theta2, theta5 = theta4 * theta;
    float theta6 = theta2 * theta4, theta7 = theta6 * theta;
    float theta8 = theta4 * theta4, theta9 = theta8 * theta;

    float f = theta + theta3 * mvParameters[4] + theta5 * mvParameters[5] + theta7 * mvParameters[6] +
                theta9 * mvParameters[7];
    float fd = 1 + 3 * mvParameters[4] * theta2 + 5 * mvParameters[5] * theta4 + 7 * mvParameters[6] * theta6 +
                9 * mvParameters[7] * theta8;
	// u = (fx * θd * x) / r + cx
	// v = (fy * θd * y) / r + cy
	// θd = θ + k1 * θ^3 + k2 * θ^5 + k3 * θ^7 + k4 * θ^9
	// θ = arctan(r,z)
	// r = (x^2 + y^2)^(1/2)
    cv::Mat Jac(2, 3, CV_32F);
    Jac.at<float>(0, 0) = mvParameters[0] * (fd * p3D.z * x2 / (r2 * (r2 + z2)) + f * y2 / r3);  // ∂u/∂x
    Jac.at<float>(1, 0) =
        mvParameters[1] * (fd * p3D.z * p3D.y * p3D.x / (r2 * (r2 + z2)) - f * p3D.y * p3D.x / r3);  // ∂v/∂x

    Jac.at<float>(0, 1) =
        mvParameters[0] * (fd * p3D.z * p3D.y * p3D.x / (r2 * (r2 + z2)) - f * p3D.y * p3D.x / r3);  // ∂u/∂y
    Jac.at<float>(1, 1) = mvParameters[1] * (fd * p3D.z * y2 / (r2 * (r2 + z2)) + f * x2 / r3);  // ∂v/∂y

    Jac.at<float>(0, 2) = -mvParameters[0] * fd * p3D.x / (r2 + z2);  // ∂u/∂z
    Jac.at<float>(1, 2) = -mvParameters[1] * fd * p3D.y / (r2 + z2);  // ∂v/∂z

    std::cout << "CV JAC: " << Jac << std::endl;

    return Jac.clone();
}