###1.什么是光束平差法
前边的八点法,五点法等可以求出闭式解的前提是已经知道确切的点对。但实际情况中往往存在大量的噪声,点与点不是精确地对应甚至出现一些错误匹配。
光束平差法由Bundle Adjustment翻译得来,有两层意思:
对场景中任意三维点P,由从每个视图所对应的的摄像机的光心发射出来并经过图像中P对应的像素后的光线,都将交于P这一点,对于所有三维点,则形成相当多的光束(bundle);实际过程中由于噪声等存在,每条光线几乎不可能汇聚与一点,因此在求解过程中,需要不断对待求信息进行调整(adjustment),来使得最终光线能交于点P。对m帧,每帧含N个特征点的目标函数如下:
(1)
其中: x ~ \widetilde x x
表示受白噪声影响的估计二维点坐标, π \pi π为投影函数,ruguo 如果点j出现在图i上,则 θ = 1 \theta = 1 θ=1,否则 θ i j = 0 \theta_{ij} = 0 θij=0。
这是一个非凸问题。
式子(1)表示对所有点
以上便是光束平差法目标函数的原理。由于场景中特征点往往较多,该问题是一个巨大的高维非线性优化问题。接下来,需要对上述式子进行求解,这是光束平差法的核心内容。
针对具体应用场景,光束平差法有不同收敛方法。目前常用的方法有梯度下降法,牛顿法,高斯牛顿法,Levenber-Marquardt等方法。
2.1 一阶方法——梯度下降法
所谓一阶方法,即对问题的目标函数进行泰勒一阶展开后进行迭代求解的方法。梯度下降法是一阶方法之一。当梯度为负值时,沿着梯度方向就是函数值f变小最快的方向。梯度下降法就是让函数沿着下降最快的方向去找函数值的最小值,就像水流沿着斜率最大的方向流去。对于变量都为标量的函数,形象的描述是始终用一条直线来拟合曲线。梯度下降法迭代式子如下:
x k + 1 = x k − ϵ d E ( x k ) / d x x_{k+1}=x_k−ϵdE(x_k)/d_x xk+1=xk−ϵdE(xk)/dx(2)
其中,ϵ表示自己设置的迭代步长,可用一维线性搜索动态确定。x表示自变量。
严格意义上,梯度下降法并不决定函数f(x)下降方向,因为它仅仅是一个余向量而非向量,只能通过最终标量的正负而非实际的向量指引函数下降方向。梯度下降法的复杂度是Ο(n),其中n为待解决问题的大小,比如矩阵E的行数。实际过程中,常常使用一维线性搜索方法来寻找合适的步长。
2.2 二阶方法——牛顿法(Newton Method)
牛顿法是二阶优化方法,即会将目标函数展开至泰勒二阶项然后进行优化求解。与梯度法相比,它们利用到了目标函数的二阶导数。形象地讲,如用牛顿法求解自变量为标量的函数时,用二次曲线来拟合最优化点时的函数曲线。
对目标函数E,其二阶泰特展开式为:
E ( x ) ≈ E ( x t ) + g T ( x − x t ) + 1 / 2 ∗ ( x − x t ) T H ( x − x t ) E(x)≈E(x_t)+g^T(x−x_t)+1/2*(x−xt)^TH(x−x_t) E(x)≈E(xt)+gT(x−xt)+1/2∗(x−xt)TH(x−xt)
(3)
其中g为E的雅克比矩阵,H为E的海塞矩阵。
由于优化点的导数为0,即:
d E / d x = g + H ( x − x t ) = 0 dE/d_x=g+H(x−x_{t})=0 dE/dx=g+H(x−xt)=0
(4)
上式展开,易知x的迭代式子为:
x k + 1 = x k − H − 1 g x_{k+1}=x_k-H^{−1}g xk+1








 本文详细介绍了光束平差法的概念,探讨了在实际应用中处理大量噪声和错误匹配点的问题。通过对目标函数的优化,涉及了梯度下降法、牛顿法、高斯牛顿法和Levenberg-Marquardt(L-M)方法。L-M算法结合了牛顿法和梯度下降法的优点,解决了高斯牛顿法中可能存在的不稳定性。文中还提到了光束平差法在多视图几何重建中的应用以及优化库的选择。
本文详细介绍了光束平差法的概念,探讨了在实际应用中处理大量噪声和错误匹配点的问题。通过对目标函数的优化,涉及了梯度下降法、牛顿法、高斯牛顿法和Levenberg-Marquardt(L-M)方法。L-M算法结合了牛顿法和梯度下降法的优点,解决了高斯牛顿法中可能存在的不稳定性。文中还提到了光束平差法在多视图几何重建中的应用以及优化库的选择。
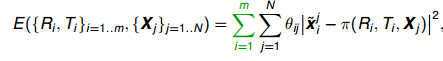
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








