老猿学5G：融合计费场景的离线计费会话的Nchf_OfflineOnlyCharging_Create创建操作

☞ ░ 前往老猿Python博文目录 ░

一、Nchf_OfflineOnlyCharging_Create消息交互流程

Nchf_OfflineOnlyCharging_Create服务化操作请求是5G融合计费的离线计费中CTF向CHF请求服务使用的初始化请求（英文原文：request initial report of service usage）。该请求操作是在UE还未存在计费数据资源的情况下发起，其过程如下：

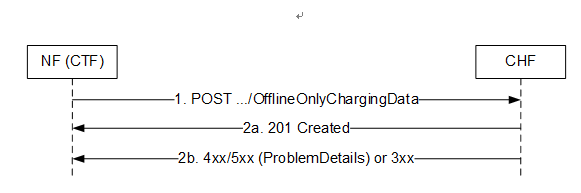
对应步骤文字描述如下：

1. CTF项CHF发送Nchf_OfflineOnlyCharging_Create request请求，要求建立开始计费的资源；
2. CHF操作成功，则回复相应消息为"201 Created"。在这个回复消息内包含了一个位置头字段（Location header field ）。位置头字段包含创建资源的URI。CTF在同一PDU会话中后续往CHF提交请求时需要使用该URI；
3. 在请求失败或重定向时，需要返回对应状态的HTTP响应码。

二、用户发起上网后的离线会话创建过程

1. 用户需要上网时，用户UE向AMF发起PDU会话建立流程，PDU会话会包含PDU会话ID、PDU类型（IPV4、IPV6等）、SSC(session and service continuity)模式、用户位置信息和接入类型
   注：在5G网络的工作模式下，用户终端通过创建的PDU会话来进行数据的通信，用户可以同时创建并使用多个PDU会话。用户终端UE通过特定的PDU会话与应用服务器建立连接，也就是采用了该PDU会话对应的SSC模式。SSC模式是用于保障用户移动场景下会话或业务的连续使用模式，有三种模式，具体可参考《5G系统——SSC模式》。
2. AMF选择SMF，并向SMF发起PDU会话建立请求（Nsmf_PDUSession_CreateSMContext Request）；
3. SMF基于基于SUPI、DNN以及默认的Qos向UDM发起用户数据请求；
4. UDM及AUSF进行用户鉴权和会话授权；
5. 在存在动态PCC策略控制的情况下，SMF选择PCF并请求PCC规则；
6. SMF选择为用户服务的UPF；
7. SMF为PDU会话选择一个SSC模式，然后相应选择一个或多个UPF；
8. SMF执行会话管理策略；
9. 当用户上网行为触发PDU会话计费事件时，SMF为该PDU会话创建ChargingID，并向CHF发送Nchf_OfflineOnlyCharging_Create消息，以授权该用户启动PDU会话；
10. CHF为该PDU会话开启CDR话单，并发送Nchf_OfflineOnlyCharging_Create响应消息给SMF，携带需要SMF触发用量上报的Trigger。
    至此一个完整的用户上网离线计费会话开启成功。

跟老猿学Python、学5G!

☞ ░ 前往老猿Python博文目录 ░