【笔记】机器人空间坐标变换

主要包括机器人空间的位姿变换以及C++编程实现

说明：本文章中的大部分图片来自南开大学-人工智能学院的《机器人学导论》课件

空间的描述

1. 位置的描述（仅笛卡尔坐标系）

在一个笛卡尔坐标系 (Cartesian coordinate)下,可以用 3 维的位置矢量来确定该空间内任一点的位置

$$P^A=[Px,Py,Pz{]}^T$$

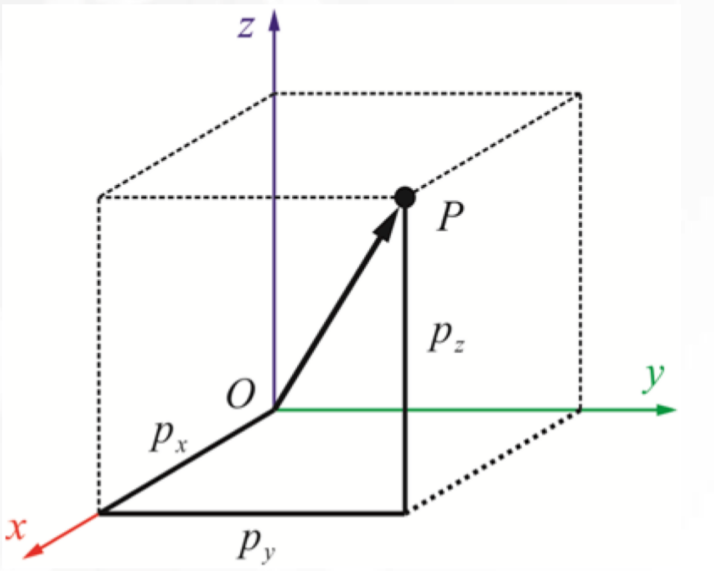
其中, $P_x,P_y,P_z$是 $P$ 点在坐标系的三个坐标轴上坐标分量

2. 姿态的描述

注意：这里只以旋转矩阵和3维平移向量为例，欧拉角和四元数后面会介绍

旋转矩阵R：$$R_B^A=[X_B^A,Y_B^A,Z_B^A]$$
$$R_B^A=\left[\begin{array}{ccc}{X}_B\cdot X_A& Y_B\cdot X_A& Z_B\cdot X_A\\ X_B\cdot Y_A& Y_B\cdot Y_A& Z_B\cdot Y_A\\ X_B\cdot Z_A& Y_B\cdot Z_A& Z_B\cdot Z_A\end{array}\right]$$

旋转矩阵的性质：

• 正交矩阵：$R_B^A={R_A^B}^{-1}={R_A^B}^T$

3. 位姿的描述

{ B } = { R B A , P B O R G A } \{B\}=\{R^A _B,P^A _{BORG}\} {B}={RBA​,PBORGA​} 其中，$P_{BORG}^A$代表$B$坐标系的原点在$A$坐标系下的位置

空间的变化

1. 平移坐标系的映射

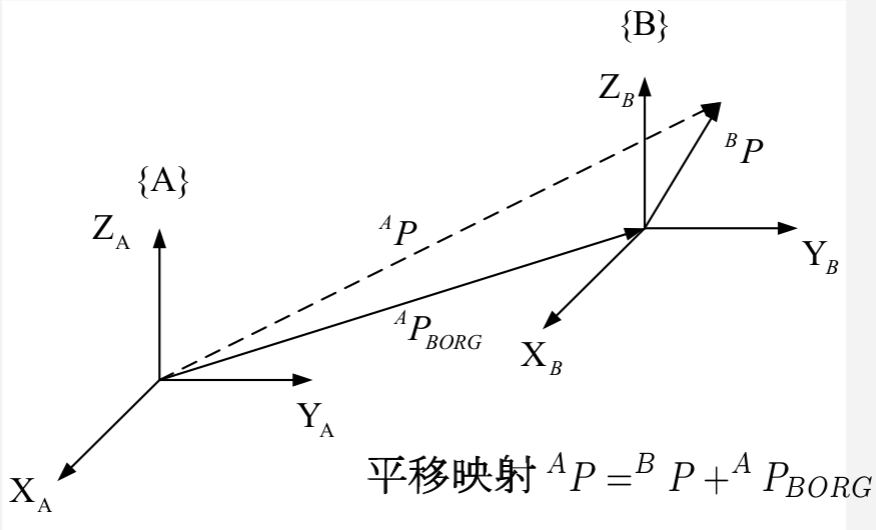
其中：$P^A$代表 { A } \{A\} {A}坐标系的原点在世界坐标系下的位置，$P^B$代表 { B } \{B\} {B}坐标系的原点在世界坐标系下的位置， { A } \{A\} {A}和 { B } \{B\} {B}之间没有旋转关系，因此只是单纯的加上平移量就可以了。

2. 旋转坐标系的映射

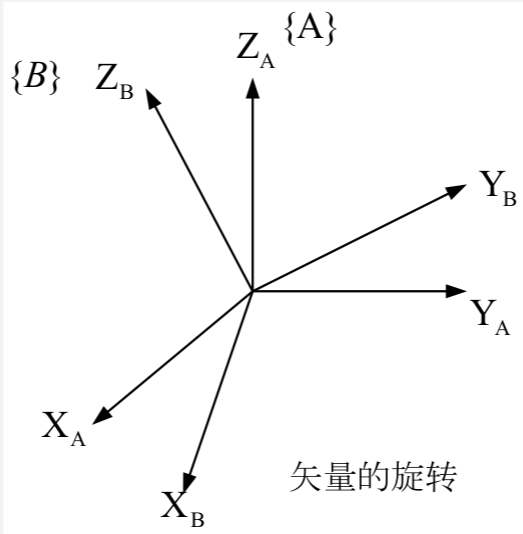
旋转映射：$P^A=R_B^A{P}^B$
其中：

• $R_B^A$代表 { B } \{B\} {B}坐标系到 { A } \{A\} {A}坐标系之间的旋转变换
• $R_B^A$各列向量模均为1，并且这些单位矢量相互正交

3. 一般坐标系的映射

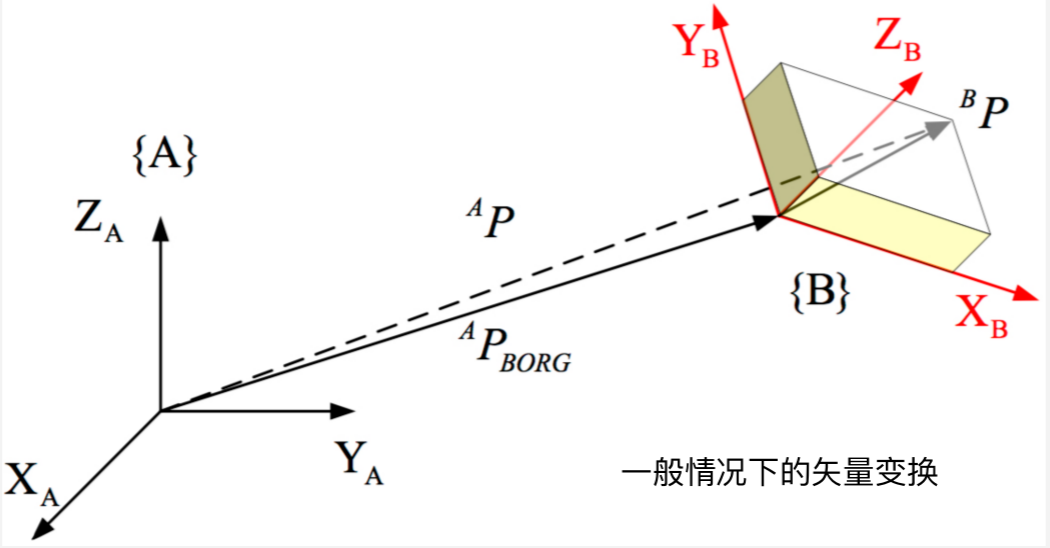
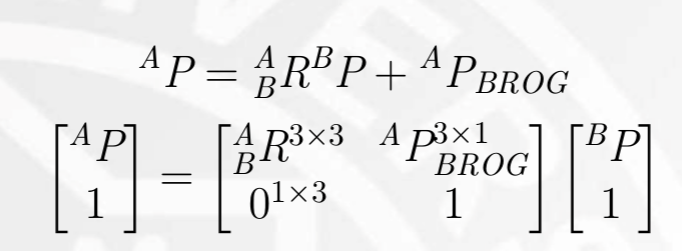
其中：

• $P^B$代表 在 { B } \{B\} {B}坐标系下$P$点的位置，$P^A$代表 在 { A } \{A\} {A}坐标系下$P$点的位置。

4. 齐次变换矩阵

其中：

• 它是坐标系的描述：$T_B^A$表示相对于坐标系 { A } \{A\} {A}的坐标系 { B } \{B\} {B}的齐次变换。（也就是坐标系 { B } \{B\} {B}变换到坐标系 { A } \{A\} {A}的变换）

5. 混合变换

第一种情况

已知 { B } \{B\} {B}坐标系到 { A } \{A\} {A}坐标系的变换$T_B^A$，已知 { C } \{C\} {C}坐标系到 { B } \{B\} {B}坐标系的变换$T_C^B$，求 { C } \{C\} {C}坐标系到 { A } \{A\} {A}坐标系的变换$T_C^A$

第二种情况

已知 { B } \{B\} {B}坐标系到 { A } \{A\} {A}坐标系的变换$T_B^A$，求 { A } \{A\} {A}坐标系到 { B } \{B\} {B}坐标系的变换$T_A^B$

注意，这里的$P_{AORG}^B$并不是单纯的加一个负号，而是等于$-{R_B^A}^T{P}_{BORG}^A$
注意，在Eigen中，求反变换只需要运用函数inverse()就可以，这里介绍的只是一种简单的求解方法。

其他姿态描述方法

Z-Y-X 欧拉角

首先将坐标系 { B } \{B\} {B} 和一个已知参考坐标系 { A } \{A\} {A} 重合。先将 { B } \{B\} {B} 绕 ${\hat{Z}}_B$ 旋转 $\alpha$ 角,绕 ${\hat{Y}}_B$ 旋转 $\beta$ 角,最后绕 ${\hat{X}}_B$ 旋转 $\gamma$ 角。
注意：欧拉角是绕着旋转后的轴旋转的，不是固定轴

编程实现

注意：

• 以下编程示例均摘自Lio-mapping
• 编程语言：C++
• 调用库：Eigen

四元数和三维向量转换为Eigen::Transform

Eigen::Transform<T, 3, Eigen::TransformTraits::Affine> transform;
// 四元数先归一化才能描述旋转
transform.linear() = rot.normalized().toRotationMatrix();
transform.translation() = pos;