二维栅格路径规划算法，全局路径规划算法包括A*，jps ，rrt，rrt*等，每种都可以单独使用

主题：智能机器人二维栅格路径规划算法

一、引言

在智能机器人的导航和路径规划中，二维栅格路径规划算法扮演着至关重要的角色。该算法能够将复杂的空间环境抽象为二维栅格地图，通过全局和局部路径规划算法为机器人提供从起点到终点的最优或可行路径。本文将针对不同的路径规划算法进行介绍，并讨论如何使用路径剪枝策略来减少路径冗余。

二、二维栅格地图生成

首先，我们需要根据图片自动生成栅格地图。这个过程通常包括图像预处理、特征提取和栅格化等步骤。通过这些步骤，我们可以将实际环境转化为二维栅格地图，为后续的路径规划提供基础数据。

三、全局路径规划算法

全局路径规划算法主要用于在已知环境中为机器人规划从起点到终点的最优路径。常见的全局路径规划算法包括A*、jps、rrt和rrt*等。

1. A算法：A算法是一种启发式搜索算法，通过评估每个节点的代价和启发式信息来选择最优路径。该算法在静态环境中表现优秀，可以快速找到最短路径。
2. jps（Jump Point Search）算法：jps算法是一种基于节点的路径寻找算法，通过快速查找跳跃点来优化路径。该算法适用于稀疏的栅格地图，能快速找到可行路径。
3. rrt（Rapidly-exploring Random Trees）算法：rrt算法是一种基于采样的路径规划算法，通过随机生长的树结构来探索整个空间。该算法适用于动态环境和复杂地形，具有较强的鲁棒性。
4. rrt算法：rrt算法是rrt算法的改进版，通过引入重连策略和剪枝策略来优化路径。该算法在保持rrt算法优点的同时，能生成更加平滑且无冗余的路径。

四、局部路径规划和动态避障

局部路径规划主要关注机器人实时的运动规划和避障。常见的局部路径规划算法包括dwa（Dynamic Window Approach）和apf（Artificial Potential Field）。这些算法可以根据机器人的实时状态和环境信息，为其规划出局部的可行路径。

在全局结合局部进行路径规划时，我们需要考虑动态避障。当机器人遇到障碍物时，应立即调整其运动轨迹，避免与障碍物发生碰撞。这需要结合全局和局部路径规划算法，以及动态传感器数据来实现。

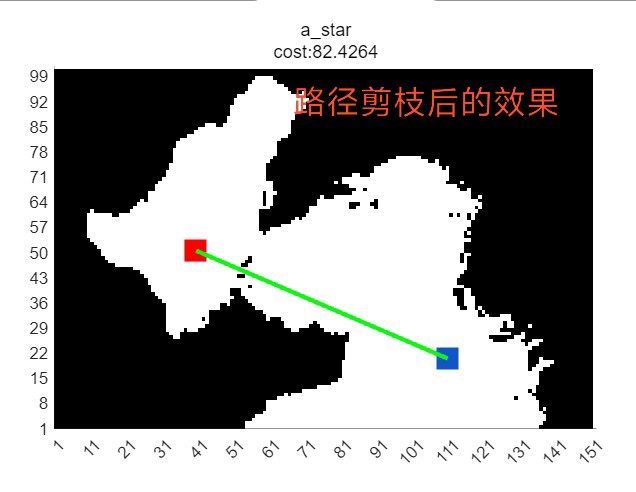
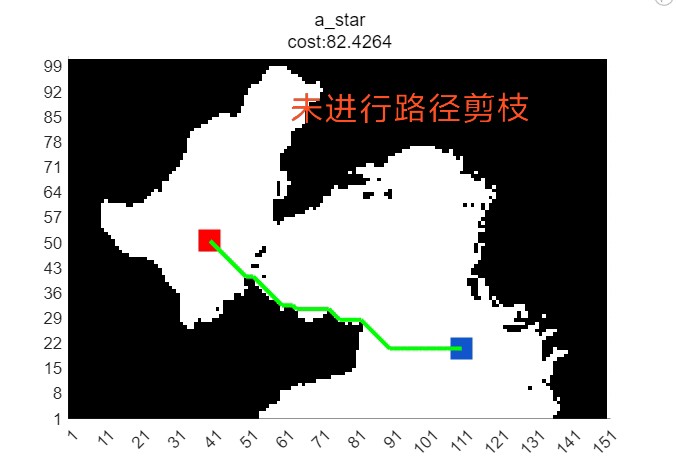
五、路径剪枝策略与减少路径冗余

为了减少路径冗余，我们可以采用路径剪枝策略。对于全局路径规划算法生成的路径，我们可以根据实际需求和机器人性能进行剪枝，去除冗余的节点和边。同时，我们还可以结合局部路径规划和动态避障信息，对全局路径进行实时调整和优化。这样不仅可以提高机器人的运行效率，还能避免不必要的能量消耗。

六、结论

本文介绍了智能机器人二维栅格路径规划算法的相关内容。通过对二维栅格地图的生成、全局和局部路径规划算法的介绍以及路径剪枝策略的讨论，我们可以为智能机器人提供更加高效、平滑且无冗余的路径。未来，随着人工智能和机器人技术的不断发展，我们期待更多的优化策略和算法被应用到智能机器人的路径规划中。
二维栅格路径规划算法，全局路径规划算法包括A*，jps ，rrt，rrt*等，每种都可以单独使用路径剪枝策略，减少路径冗余。
局部路径规划有dwa和apf算法。
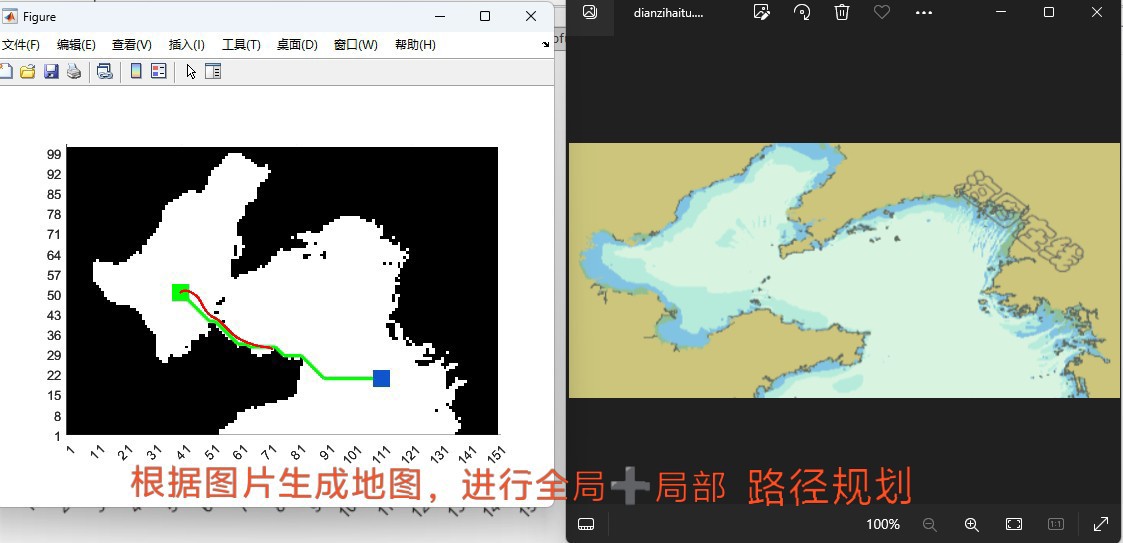
可以根据图片自动生成栅格地图，全局结合局部进行动态避障，示意图如下。
局部路径贴合全局路径