【鱼眼镜头6】[鱼眼畸变模型]：统一相机模型标定scaramuzza多项式模型

我们需要先来说几个名词解释

1、相机畸变误差：获得的图像，与理论上的投影模型输出结果的偏差
2、标定算法：根据相应的投影模型，设计了一套算法，计算让相机畸变误差最小的一组参数。

1、相机投影模型

通常根据应用场景的不同，将相机等效为以下的几种模型：为了描述成像原理。

一句话理解：目标点与图像点之间的像素映射关系

1、针孔相机模型（透视投影模型）

a pinhole camera (perspective camera)
对于一般的小孔成像模型其成像的示意图如下所示。一般鱼眼镜头不是这种方式。

2 、 经度坐标投影

有一种全球地图展开法的含义。

经度坐标校正就是把鱼眼图像中像素的横坐标变换到原来的位置，而纵坐标不变，通过这样的变换会把圆形的鱼眼区域变换成正方形。下图（来源于《一种不断重定位圆心的鱼眼图像校正方法》）明确阐述了其中的原理，鱼眼图像中心坐标为O(x0,y0)，半径为R，A(x,y)是在圆形畸变区域边上的一点，B(u,v)是其经过校正后的坐标，其中B点肯定会位于校正后正方形的右边上。

3、统一模型

我们如果不关注实际内参。可以提出抽象模型。

一种抽象的相机投影模型，我们定义一个矩阵M来表示。相机被视为一个独特的紧凑系统，M封装了相机的内在参数和镜子的参数。我们通过标定算法求解M，我们并不关注具体的内参是情况。

中央全向相机，即任何具有单一有效视点的全景相机

• central omnidirectional camera, that is, any panoramic camera having a single effective viewpoint

不需要关于镜子形状的先验知识

它不需要单独校准透视相机：系统相机镜被视为一个独特的紧凑系统，它封装了相机的内在参数和镜子的参数。

2、标定算法

不同角度的镜头有不同的畸变模型，比如多项式模型就适合视角比较小的镜头，分式模型或者scaramuzza多项式模型就适合视角比较大的镜头

这些模型都是去逼近实际镜头的畸变，畸变程度比较小的时候用的是传统多项式模型，畸变程度比较大的时候用分式模型或scaramuzza多项式模型

而无论是opencv还是matlab的标定工具箱，都有两种标定工具，一种是传统的视角比较小的相机标定，另外一种fisheye camera calibration。所以从这里也能够看出来区别，就是鱼眼相机不能够用传统的多项式进行标定

2.1、 小孔成像模型

视角比较小 一般可以用 张正友的标定工具箱
这个比较通用，其实不适合用于鱼眼镜头标定

2.2、基于等距模型的球面透视投影模型

基于球面投影的理论模型，进行优化了投影计算。模组厂商会根据投影模型设计镜片组。

基于等距模型的球面透视投影的方法，建立5个坐标系：世界坐标系，摄像机坐标系，成像平面坐标系，图像图标系，像素平面坐标系。这5个具体的坐标系共同组成了一个完整的成像系统。

输出的结果：

• 获取摄像机的外参和内参，
• 外参包括摄像机的旋转矩阵，平移矩阵。
• 内参主要是摄像机的焦距以及畸变半径的修正参数。当然了除了这几个参数之外我们同样需要获取成像平面到图像坐标系平面的高度。以及成像平面到世界坐标系之间的高度。对于这些参数我们需要使用不同的标定板来得到。

鱼眼图像畸变半径的粗略估计：
基本思想是通过过图像处理的方式获得ROI区域。然后对ROI区域求解半径。
大致的方案：
二值化，形态学操作，连通域获取，最大外接矩形，半径计算，参数输出

参考：https://blog.csdn.net/Gavinv/article/details/78506788

2.3、scaramuzza多项式模型（统一相机模型）

在 scaramuzza 之前，统一投影模型（Unified Projection Model）由Geyer和Daniilidis在2000年提出，后来被Barreto和Araujo进一步改进。它的特点是能够涵盖使用双曲面、抛物面或椭圆面镜子的所有三种类型的中央折反射相机。尽管统一投影模型最初是为中央折反射相机设计的，但研究人员已经尝试将其用于近似描述鱼眼相机的成像过程。然而，由于鱼眼相机的成像原理与折反射相机存在本质差异（如折射效应），因此这种近似通常只具有有限的准确性。

Taylor模型由Scaramuzza等人于2006年开发，旨在统一描述中央折反射相机和鱼眼相机的投影过程。

推荐scaramuzza的畸变校正toolbox（https://sites.google.com/site/scarabotix/ocamcalib-omnidirectional-camera-calibration-toolbox-for-matlab）（http://rpg.ifi.uzh.ch/people_scaramuzza.html），是专门有两篇iros论文介绍这个工具箱。

scaramuzza 的全方位相机模型

校准全向相机意味着要找到给定的 2D 像素点 p 与从镜面有效视点发出的 3D 矢量 P 之间的关系（见下图）。 一般情况下，这个过程需要找到相机内参和镜子内参。

我们的全向相机模型将成像系统视为一个独特的紧凑系统； 也就是说，它并不关心您是将镜子还是鱼眼镜头与相机结合使用。

我们的模型基于以下假设：

1、镜面相机系统是一个中心系统，因此在镜面中存在每条反射光线相交的点。该点被认为是相机坐标系XYZ的轴原点。

2、相机和反射镜轴对齐良好，即模型中只考虑了很小的旋转偏差。

3、反射镜相对于其轴旋转对称。

4、模型中没有考虑相机的镜头畸变。相机镜头畸变没有被包括在内，因为使用镜子的全向相机通常需要大焦距f才能将图像聚焦在镜子上。因此，镜头畸变真的可以忽略不计。如果您使用鱼眼镜头，camera lens distortion is already integrated in the projection function f.。

19.2 全向相机模型：部分模型解释

现在，我将解释全向相机模型。

现在，让我们假设假设 2 得到完美验证，即相机和镜轴完全对齐。稍后，我们将看到如何克服这种限制。

设 p 为图像的像素点，以及 (u,v) 其相对于全向图像中心的像素坐标（见下图）。设 P 是从单个有效视点发出的相应 3D 矢量，以及 (x,y,z) 其相对于轴原点的坐标。

因为相机轴和镜轴应该完全对齐，所以观察 x 和 y 分别与 u 和 v 成比例。因此，

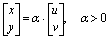
我们希望校准估计的函数是将图像点 p 映射到其对应的 3D 矢量 P 的函数。所以我们可以写：

您可能已经观察到，我们可以将 α 包含到函数 f 中，因此我们可以同样写成：

确实，请记住 P 不是一个 3D 点，而是一个向量；因此最后的简化是允许的！

此外，因为镜子是旋转对称的，所以函数 f(u,v) 仅取决于点到图像中心的距离 。
因此，我们仍然可以将前面的等式简化为以下等式：

如果你明白我到目前为止所解释的，我们需要校准的只是函数 f(ρ)。现在，让我们来介绍一下这个功能是什么样的。

我们的模型通过多项式描述函数 f(ρ)，其系数是要估计的校准参数。那是：

所以要估计的参数是：a0, a1, a2, a3, a4, … 实际上，OcamCalib Toolbox 要求指定您要使用的多项式次数。实际上，多项式阶数增加得越多，校准的准确性就越高。对于高阶多项式，情况并非如此。通过大量使用这个工具箱，我体验到四阶多项式给出了最好的校准结果。

19.3 全向相机模型：完整的模型解释

如果您还记得，到目前为止，我们假设相机轴和镜轴完全对齐。实际上，由于相机镜设置中的自然误差，可能会出现与此假设的微小偏差。而且，由于相机的数字化过程，像素可能不是方形的。

这些问题的自然后果是，镜子的圆形外边框看起来像一个椭圆，如下图所示（此图中的失真效果已被有意强调）。

为了考虑到这些因素，我选择通过仿射变换对错位误差和数字化伪影进行建模：

该方程将真实的失真坐标 (u’,v’) 与理想的未失真坐标 (u,v) 相关联。