线性代数——欧拉角，旋转矩阵和四元数的关系

目录

欧拉角转旋转矩阵(右手定则逆时针旋转)

欧拉角转旋转矩阵(左手定则顺时针旋转)

旋转矩阵转欧拉角

四元数转旋转矩阵

旋转矩阵转四元数

四元数转欧拉角

参考网址: https://www.zhihu.com/search?type=content&q=%E5%9B%9B%E5%85%83%E6%95%B0%EF%BC%8C%E6%AC%A7%E6%8B%89%E8%A7%92%E5%92%8C%E6%97%8B%E8%BD%AC%E7%9F%A9%E9%98%B5

---

欧拉角转旋转矩阵(右手定则逆时针旋转)

因此，从一个坐标系oxyz 转换到另一个坐标系txyz， 转换矩阵为:

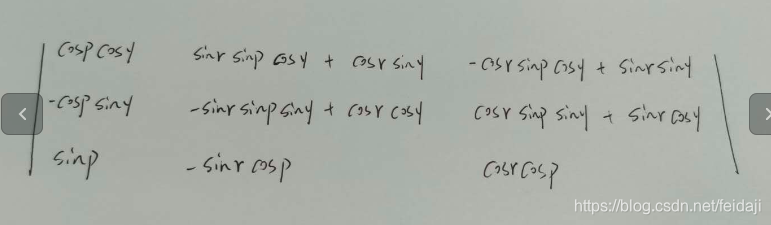
欧拉角转换乘矩阵，一个点(1,0,0) 从一个坐标系转换到另一个坐标系下的例子如下

(自己写的初始例子)

#include <iostream>
#include <cmath>
using namespace std;
/*
作用：2个3x3 矩阵点乘，
输入: 3x3矩阵m1, 3x3矩阵m2
输出:  矩阵m1 点乘 m2 后的3x3 矩阵m_target
*/
void matrixDot(float m1[][3], float m2[][3],float (*m_target)[3] )
{
    //float m_target[3][3];
    m_target[0][0]=m1[0][0]*m2[0][0]+m1[0][1]*m2[1][0]+m1[0][2]*m2[2][0];
    m_target[0][1]=m1[0][0]*m2[0][1]+m1[0][1]*m2[1][1]+m1[0][2]*m2[2][1];
    m_target[0][2]=m1[0][0]*m2[0][2]+m1[0][1]*m2[1][2]+m1[0][2]*m2[2][2];

    m_target[1][0]=m1[1][0]*m2[0][0]+m1[1][1]*m2[1][0]+m1[1][2]*m2[2][0];
    m_target[1][1]=m1[1][0]*m2[0][1]+m1[1][1]*m2[1][1]+m1[1][2]*m2[2][1];
    m_target[1][2]=m1[1][0]*m2[0][2]+m1[1][1]*m2[1][2]+m1[1][2]*m2[2][2];

    m_target[2][0]=m1[2][0]*m2[0][0]+m1[2][1]*m2[1][0]+m1[2][2]*m2[2][0];
    m_target[2][1]=m1[2][0]*m2[0][1]+m1[2][1]*m2[1][1]+m1[2][2]*m2[2][1];
    m_target[2][2]=m1[2][0]*m2[0][2]+m1[2][1]*m2[1][2]+m1[2][2]*m2[2][2];

    //return m_target;
}

/*
作用：点point 左乘旋转3x3矩阵matrix, 从一个坐标系转换到另一个坐标系的点
输入: 3x3旋转矩阵matrix, 起始点point， 是一个3x1的矩阵
输出: 3x1 目标点target_point 
*/
void matrixDot(float matrix[][3], float point[][1],float (*target_point)[1] )
{
    //float m_target[3][3];
    target_point[0][0]=matrix[0][0]*point[0][0]+matrix[0][1]*point[1][0]+matrix[0][2]*point[2][0];
    target_point[1][0]=matrix[1][0]*point[0][0]+matrix[1][1]*point[1][0]+matrix[1][2]*point[2][0];
    target_point[2][0]=matrix[2][0]*point[0][0]+matrix[2][1]*point[1][0]+matrix[2][2]*point[2][0];
}

/*
作用: 欧拉角转换成旋转矩阵，顺序是先绕x轴逆时针(正向)旋转roll 角， 再绕y 轴逆时针旋转pitch 角
      最后绕z轴逆时针旋转yaw 角，注意必须按顺序旋转，顺序不同，结果不一样
参数&#x