向量代数：向量的内积和外积

一. 内积

        定义：两个向量 a与 b的内积为 a ·b = |a||b|cos∠(a, b)，它是数量而不是向量。

特别地，0·a =a·0 = 0；若a，b是非零向量，则a与b正交的充要条件是a·b = 0。

       几何意义：a·b等于向量a在b上的投影πb(a)与b的长度之积：a·b = |b|a·(b/|b|) = |b|πb(a)。

        性质：

1. a^2 ≥ 0；当a^2 = 0时，必有a = 0.                         （正定性）
2. a·b = b·a.                                                                    （对称性）
3. (λa + μb)·c = λa·c + μb·c，对任意实数λ, μ成立. （线性）
4. cos∠(a,b) =a·b/(|a||b|).
5. |a·b| ≤ |a||b|，等号只在a与b共线时成立.

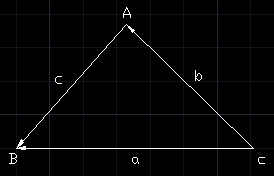
        余弦定理：在△ABC中，成立 c^2 = a^2 + b^2 - 2abcosC，如下图所示：

二. 外积

         定义：向量 a与 b的外积 a× b是一个向量，其长度等于| a× b| = | a|| b|sin ∠(a,b)，其方向正交于a与b。并且，(a,b,a×b)构成右手系。

特别地，0×a = a×0 = 0.此外，对任意向量a，a×a=0。

        几何意义：a与b的外积在数值上等于以a,b为邻边的平行四边形的面积。

        基本性质：

1. a × b = -b × a.                                   （反称性）
2. (λa + μb) × c = λ(a ×c) + μ(b ×c). （线性）

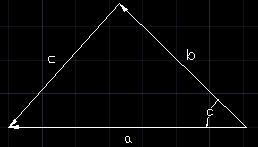
        正弦定理：a/sinA = b/sinB = c/sinC，如下图所示：

三. 参考

[1] 苏步青. 空间解析几何. 上海：上海科技出版社，1984