将旋转朝向运动

最新推荐文章于 2025-04-02 21:54:44 发布
最新推荐文章于 2025-04-02 21:54:44 发布
阅读量1.8k 收藏 2
点赞数
分类专栏： UE4自学 文章标签： 虚幻4 UE4 虚幻引擎4
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/learning_unreal/article/details/107239277
版权
本文探讨了在虚幻4（UE4）中，如何理解和使用'将旋转朝向运动'功能。通过实验，作者发现 pawn（character）与 actor 在旋转时的关系，并解释了在开启该功能后，如何通过控制器旋转影响角色朝向。实验展示了actor的旋转会根据鼠标输入和'将旋转朝向运动'调整，而pawn则不再转动，进一步揭示了UE4中的角色运动逻辑。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

这篇日志是对第一篇的否定，即pawn不是角色脚底下相连的控制物，在人物蓝图中，pawn就是包括人物基础actor在内的character类，是个特殊的pawn。

公式pawn（character）=actor+controller

那个脚底下的东西应该是controller，但这个应该没有和actor连着

然后针对将旋转朝向运动的功能理解，我做了个量化比较实验。

首先要有三个打印文本

人物蓝图中的“获取控制旋转”

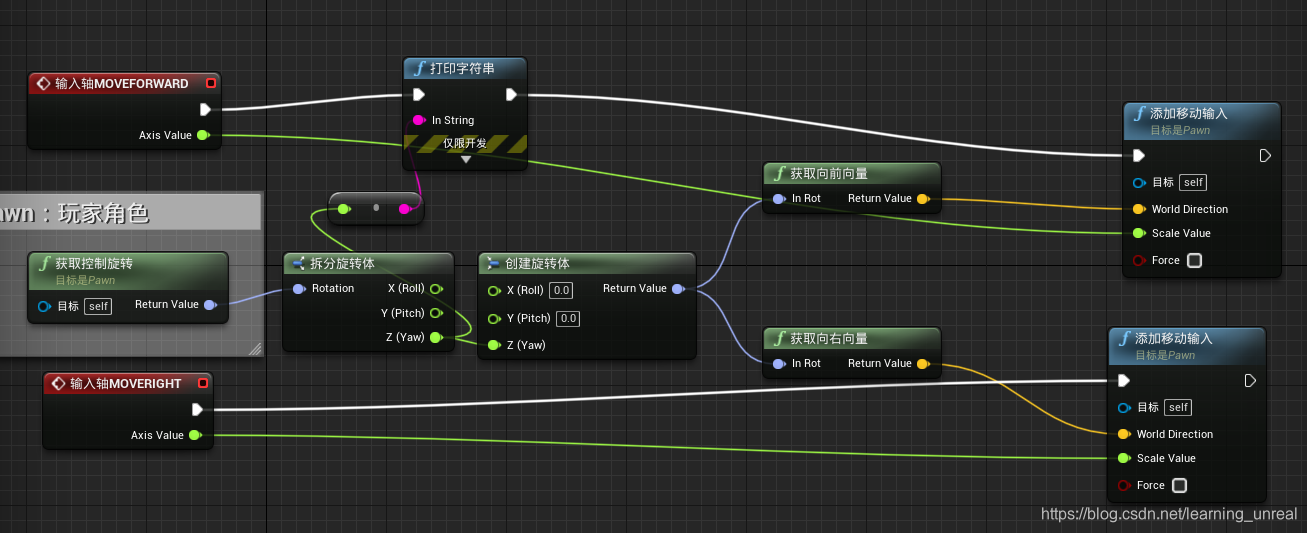
动画蓝图中的“获取控制旋转”与“获取actor旋转

 

 

 

 

 

 

 

 

 

**有点杂乱，不过不影响，这实现的功能就是人物根据”wasd“按键形成行走动画+头部随鼠标有左顾右盼上仰下探的动画动作

只需要关注”获取控制旋转“到后面的”打印文本“以及”获取actor“旋转到后面的打印文本

前提是除了第一张蓝图实现的”wasd“运动蓝图外外，你还编写好了靠鼠标变换视角的事件蓝图

然后先将摄像机设置全打勾（人物蓝图——springarm——细节面板——摄像机设置）

将chara

最低0.47元/天 解锁文章
UE4“将旋转朝向运动”、人物蓝图springarm的细节面板中“相机设置——使用pawn控制旋转、类默认值中pawn的旋转属性：三者间的辨认
learning_unreal的博客
07-08 4049
我是个非常喜欢虚幻4的小白，只是想分享一些我在学习虚幻4中的一些心得和对专有名词的个性化理解，鄙人不才，虽然实现了“目标偏移”和“人物静止时看得到脸，运动时看不到脸”的功能，不过还只停留在记忆层面。我是很想知道原理的人，所以思考过后，决定从整个“旋转”方面入手，这两天就被标题中的三个设定所困扰。 核心问题就是pawn到底该如何理解，它到底是个什么东西，我用了组控制变量实验，在文末我会阐明实验的准备工作并放上最能指明pawn的两个实验，喜欢的就鼓励鼓励，哪里错了也请指正。 为了方便我自己或者是各位读者理解
将旋转朝向运动与使用控制器控制pawn的旋转
learning_unreal的博客
07-10 2850
直接放简化后的结论 将旋转朝向运动：键盘决定正前方 类默认值里的使用控制器xx旋转：鼠标控制正前方。 原因：本质上控制的是pawn，然后联动人物静态网格 从程序上讲： 键盘控制pawn蓝图： 鼠标控制pawn蓝图： pawn属性： 鼠标控制蓝图控制的pawn指向的就是类默认值里的pawn，因为鼠标控制蓝图中的蓝色封装函数与该属性框中的“使用控制器旋转...
虚幻引擎控制角色跟随移动方向旋转的方法
woshihedayu的博客
04-02 820
在UE5中，要控制角色随移动方向旋转，可以使用蓝图和C++两种方式来实现。
ue4 旋转指定方向
11-20 5714
使用make rotator 加 combineRotators 可实现旋转指定方向（x或y或z）
UE4_旋转节点总结二——实现盯着某物或者看向相同方向功能
Growthofnotes的博客
03-28 1467
如何利用旋转等蓝图节点完成Actor与Actor看向相同的方向或者一个Actor看向另一个Actor的方法。
UE4中物体的旋转位移方法总结大全
热门推荐
UE4Learner的博客
10-08 1万+
一:UE4中物体的旋转 在开始之前我要介绍一些准备知识. 如下图所示: 在空间变换中物体的旋转有三个情况: 分别对应X轴旋转,Y轴旋转,Z轴旋转,对应起来就是roll, pitch, yaw. 以飞机的空间运动我们可以称:roll—翻滚角,yaw—航向角 ,pitch—为俯仰角 如图ue4 中物体的旋转都需要用到前面介绍的知识，所以我们必需要了解，下面我介绍一下如何控制物体的旋转. 如下图所示: ue4中这些函数可以控制物体在任意方向旋转,但是这几个函数看起来虽然相似但是有区别,当然这种函数还有很多
理解旋转姿态朝向等术语
07-06
在计算机图形学和游戏开发中，旋转、姿态和朝向是至关重要的概念，它们影响着3D对象如何在虚拟空间中定位和运动。Jim Van Verth作为Insomniac Games的高级引擎程序员，在GDC（游戏开发者大会）上介绍了一篇关于理解...
斯坦福UE4 + C++课学习记录 4：控制旋转
weixin_51524146的博客
06-26 1203
PlayerPawn3. 还需要把Player的“”中的“”勾选，这样当我们在按A/D左右移动时，角色会转向相应的方向，而不是斜着身子偏移（像那种2D接球游戏也许就不用开这个选项）
虚幻5|角色原地旋转动画
djh7758258520184的博客
08-03 884
2.在序列上方添加以上蓝图，获取控制旋转get control rotation和get actor rotation，这很符合逻辑，我们要获取鼠标（摄像机）旋转和角色的旋转。若大于90度，就会向右转，我们的控制器就会被使用，一般控制器是控制xyz轴，但一般默认使用z(yaw),朝向为否，小于90度也如此。当转完角度后，我们就会归零，这条分支知道我们归零，就会取消控制器，朝向运动，左转右转的所有值。4.讲一下x,y,z，往往是立体方向，我们的z就是平面方向，向右转动，z轴的角度就会变化。
UE5学习记录 (3)——不同人称视角下的摄像机
xxxxx666666的博客
11-28 2095
总结一下主要有以下两点1.如果希望通过摄像机的视角控制角色的朝向（第一人称模式），你需要*勾选角色细节面板下的Pawn中的使用控制器旋转属性。*勾选角色旋转面板下的使用控制器所需的旋转（此项搭配控制器使用，使得当摄像机视角告诉变化时，角色能平滑旋转）2.如果希望使用输入运动来控制角色的朝向（第三人称模式），你需要*取消勾选角色细节面板下的Pawn中的使用控制器旋转属性。*勾选摄像机弹簧手臂细节面板下的使用Pawn控制旋转和继承Pitch Yaw Roll*勾选角色细节面板下的。
UE4 RPG游戏AI制作笔记——AI移动向量
Like_Feigling的博客
04-28 651
AI混合空间值 左为负，右为正 AI蓝图 获取控制旋转-打印字符串后显示目标处于AI世界的方向角度值 世界角度值不变 x向量中的旋转-打印字符串后显示目标处于AI相对的方向角度值 相对角度值随AI向量发生改变 设黑坐标轴为世界坐标轴，红坐标轴为AI坐标轴 ...
90天入门UE引擎开发--学习日记(31/100)
weixin_42229060的博客
09-25 1314
路径前面如果有黄色感叹提示，说明本视频只是通过地址来访问的，并未真正导入，打包工程时也不会有这个视频。（ue4只支持简单的mp4、avi等视频的导入渲染，更高清的需要用到解码器。二：警戒状态：警戒范围内灯光变红，触发警报，锁定目标。​​​​​​​闪光灯类蓝图中写由接口触发的事件。接口的概念：对象给别的对象插上接口，传递信息。接口的概念：对象给别的对象插上接口，传递信息。方法1：创建变量（吃金币得分的关联）（摄像机把人物的距离信息告诉门和灯）方法1：创建变量（吃金币得分的关联）里面调用接口：​​​​​​​。
UE4 拖拽Actor移动和旋转
qq_41919347的博客
11-25 2311
移动端上通过触控对Actor进行控制，上半是拖拽移动，下半是在屏幕上滑动控制旋转。 因为是Actor，记得在BeginPlay打开控制。
UE4 在Tick中使用插值旋转物体，InterpTo系列
ZhangjieZzJ的博客
08-08 8260
目标是使敌人始终面向玩家，但是又不能转得过于生硬，需要带点阻尼的效果。 敌人朝向玩家：FindLookAt() 使用findLookAtRotation()，通过输入的两个世界坐标得到一个旋转。 实际上是调用如下的函数： KISMET_MATH_FORCEINLINE FRotator UKismetMathLibrary::FindLookAtRotation(const FVector&am...
UE4的旋转笔记
nosix的博客
09-13 1万+
--=== 2016.09.13 ===-- 最近想将一个vector转化为rotator，转而需要考虑UE4到底是怎么旋转的。 下面我们做个实验： 我们先将两个staticMesh放入场景，并将它们的rotation调成一样，如上图。 上面那个为renti_a_gear，下面那个为renti_a_gear2. 第一种情况： 绕自身坐标系来旋转 如上图，两个static
UE4 回合游戏项目 15- 生成玩家、控制玩家
ChaoChao66666的博客
11-10 3155
​在上一节（UE4 回合游戏项目 14- 添加敌人攻击）基础上继续完成生成玩家、控制玩家移动的功能。
UE4-4.26蓝图功能实现：按键控制物体旋转（蓝图通信触发自定义事件）
Jaeger719的博客
02-20 4645
1.创建一个蓝图类actor，随便添加一个旋转的物体组件 并在蓝图中单独将它拖拽出来，因为我们不希望整个类都跟着旋转，只想要里面的某个物体进行旋转 添加一个本地旋转的节点功能，另外希望他是按Z轴数值旋转的所以在Z轴添加一个旋转数值 另外还要添加个事件Tick（每帧调用），不然的话只旋转1次就停了 不会一直旋转，目的就是去每帧调用执行该事件 接着我们需要用到布尔值（true/false）去控制旋转，添加一个变量改个名叫是否可以旋转，然后再细节栏设置为布尔类型，默认值记住不能打勾否则一开始布尔值就为tr
UE4 鼠标控制旋转（2）
weixin_42399500的博客
04-02 1876
限制Y轴的旋转，X轴360度随意选转
UE 实现镜头平移，旋转和缩放
netcy的专栏
09-02 9352
在原来的Z轴旋转的基础上，加上一个增量，这个增量就是“鼠标X”节点的Axis Value，不过一般来说，Axis Value 会比较小，所以还会先乘以一个倍数，把相称的结果作为增量。其中目标是Pawn类，此处使用self即可（Pawn类自身，World Direction表示移动的方向，Scale Value 表示移动的缩放值，一般1表示向前，-1向后，这个正好和前面的Axis Value可以对应。在监听了鼠标X事件后，需要设置镜头的旋转，通过下面的蓝图节点，可以设置Pawn的旋转。
旋转轴 三维运动运动插补
最新发布
04-25
### 3D旋转轴运动插补算法概述 在三维空间中，旋转轴的插补通常涉及复杂的几何运算以及坐标变换。为了实现精确的路径规划和控制，常见的方法包括基于矢量分析、矩阵变换或者利用数值逼近技术（如泰勒级数展开）。以下是几种典型的插补算法及其应用： #### 圆弧插补 圆弧插补是一种常用的曲线插补方式，在二维平面上已经得到了广泛应用[^2]。将其扩展至三维空间时，可以通过定义旋转中心点 \(C\) 和半径 \(R\) 来描述一条完整的圆弧轨迹。 假设目标是从起点 \((X_s, Y_s, Z_s)\) 到达终点 \((X_e, Y_e, Z_e)\)，并绕某一固定轴向量 \(\vec{n}\) 转动，则可以按照以下步骤计算中间位置： 1. **确定旋转角度** 计算两点之间的夹角 \(\theta\) 使用叉积公式：\[ \cos{\theta}=\frac{(X_e-X_s)(Y_e-Y_s)+(Z_e-Z_s)}{||P_{se}||} \] 2. **分段处理** 将整个圆周划分为若干个小段，每一段对应一个小的角度增量 \(\Delta\theta_i\) 。通过逐次累加这些微小变化来逐步接近最终目的地。 3. **更新当前位置** 对于每一帧时间间隔 t ，依据当前累积转过的总度数重新定位新的坐标系下的 X',Y' 及 Z 值，并映射回原始世界框架下得到实际移动后的物理座标。 ```python import math def spherical_interpolation(start_pos, end_pos, num_segments=100): """球面线性差值(Slerp),用于生成两个四元组间的均匀过渡序列""" q_start = start_pos / np.linalg.norm(start_pos) q_end = end_pos / np.linalg.norm(end_pos) dot_product = sum([a*b for a,b in zip(q_start,q_end)]) omega = acos(dot_product) sin_omega = sqrt(1-dot_product*dot_product) results = [] if abs(sin_omega)<epsilon: # 如果几乎共线则退化成LERP step_size=(end_pos-start_pos)/num_segments for i in range(num_segments+1): interpolated_point=start_pos+i*step_size results.append(interpolated_point.tolist()) else: factor_a=[sin((1-t)*omega)/sin_omega for t in linspace(0.,1.,num=num_segments)] factor_b=[sin(t*omega)/sin_omega for t in linspace(0.,1.,num=num_segments)] for fa,fb in zip(factor_a,factor_b): intermediate=farray(fa*q_start)+farray(fb*q_end) normalized_intemediate=intermediate/np.linalg.norm(intermediate) results.append(normalized_intemediate.tolist()) return array(results,dtype=float64) # Example Usage start_orientation = [-0.5,-0.8,0.2] goal_orientation = [0.9,0.4,-0.1] path_points=spherical_interpolation(array(start_orientation),array(goal_orientation)) print(path_points[:5]) # Print first five points along path. ``` 此代码片段展示了如何使用 Spherical Linear Interpolation (SLERP)[^2] 方法来进行方向上的平稳转换，这对于保持物体朝向的一致性和连贯性非常重要。 #### 多轴协同工作模式下的插补策略 当涉及到多个相互关联的动作单元同步运作时——比如 CNC 加工中心里的 XYZT 四自由度联动操作——就需要考虑更高级别的协调机制了[^3]。这里提到的一个关键技术要点就是所谓的 “主从关系”，即指定某条轨道作为主导者而其他跟随其节奏调整各自步伐大小；如此一来便能确保整体动作流畅自然无突兀感。 另外值得注意的是，在某些特殊场合还需要引入额外的功能模块诸如前视缓冲区管理器等辅助工具以便更好地应对可能出现的各种突发状况比如说急转弯等情况下的速度调节问题等等[^4]。 ---
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值