【PLL】分数锁相环：分数N频率合成

最新推荐文章于 2025-05-13 20:33:05 发布

opcode0

最新推荐文章于 2025-05-13 20:33:05 发布

阅读量1k

点赞数 14

分类专栏： PLL 文章标签：学习例子

本文链接：https://blog.csdn.net/m0_62489442/article/details/146097781

版权

PLL 专栏收录该内容

38 篇文章

订阅专栏

在传统的基于锁相环（PLL）的频率合成器中，相位检测器（PD）频率确定最小步进频率。

因此，PD频率通常由无线系统的信道间隔要求来设置。

设计一个高性能的PLL对于大分频比是相当具有挑战性的。

小数N分频PLL的开发是为了在相同的频率分辨率下使用高PD频率，从而可以显著降低分频比。

分数N频率合成是基于数字相位控制方法完成的，
该方法最初被称为数字相位技术，
后来被命名为用于商业产品的分数N技术。

分数N频率合成器的发展大大提高了现代收发系统的性能，不仅作为低噪声本机振荡器，而且作为直接数字频率调制器。

1. 基本原理

分数分频比可以通过调制双模分频器的控制输入来获得，这基本上是频率内插。

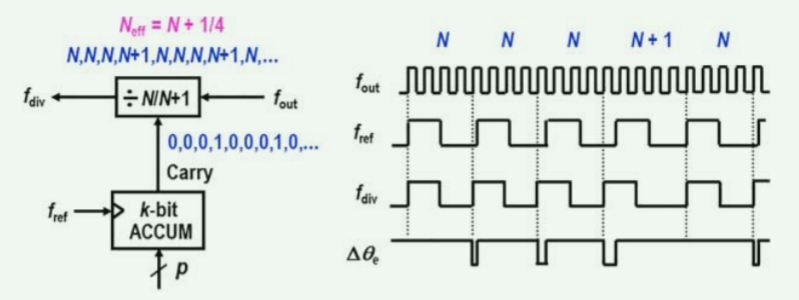
使用N/（N+ 1）双模分频器实现（N+1/4）小数分频比

为了具有（N+ 1/4）的分频比，
对于每三个N分频进行一次（N+ 1）的分频比。
2位累加器用于生成{.000100010001...}的进位序列
其中进位输出“1”对应于（N+ 1）分频。

输出时段Tout和参考频率Tref通过相关：

$T_{ref}=T_{out}(N+\frac{1}{4})=NT_{out}+\frac{T_{out}}{4}$

由于除以N引起的瞬时相位误差是：

$\Delta t_N=T_{ref}-NT_{out}=\frac{1}{4}T_{out}$

由于除以N+1引起的瞬时相位误差是：

$\Delta t_{N+1}=T_{ref}-(N+1)T_{out}=\frac{3}{4}T_{out}$

每个参考周期的瞬时相位误差:

$\{...,+\frac{1}{4}T_{out},+\frac{1}{4}T_{out},+\frac{1}{4}T_{out},-\frac{3}{4}T_{out},...\}$

输出频率：

$f_{out}=(N+\frac{p}{2^k})f_{ref}=Nf_{ref}+\frac{p}{2^k}f_{ref}$

p是在 $2^k$ 个时钟周期的为“1”的个数

k-bit的累加器的频率分辨率：

$\Delta f=\frac{p}{2^k}f_{ref}$

增加累加器的位数，可以实现更精细的频率分辨率。

由于PD频率高于小数N分频PLL的频率分辨率，因此环路带宽不受频率分辨率的限制。

小数N分频PLL周期性调制双模分频器来产生平均输出频率。
调制周期对应于参考频率的分数，将基于窄带频率调制（FM）生成杂散
结果，在载波和参考杂散之间产生接近杂散，即分数杂散。
与取决于电路失配或漏电流的基准杂散不同，数字相位控制引起的分数杂散被视为系统调制，
其电平可以通过了解PLL参数来估计

example 计算分数杂散电平

PLL使用8/9双模分频器和2位累加器

从20 MHz参考频率生成165 MHz输出频率，8.25的有效分频比

小数杂散将出现在160和170 MHz处，这是载波频率的5 MHz偏移频率。

8/9双模分频器的输出用作2位累加器的时钟。

电荷泵电流为100 μA
（VCO）增益为100 MHz/V
环路带宽为1 MHz，R1 = 5.2k Ω，C1 = 150 pF，C2 = 15 pF。

估计5 MHz偏移频率下的分数杂散电平。

最大相位偏差：

$\Delta \theta_{pk}=\frac{1}{2}*\frac{3}{4}T_{out}*\frac{2\pi}{T_{ref}}=\frac{3\pi}{4}\frac{T_{out}}{T_{ref}}=\frac{3\pi}{4}\frac{1}{N_{eff}}$

Neff：有效分频比

峰值频率偏移：
$\Delta f_{pk}=a_1*\Delta \theta_{pk}*\frac{I_{CP}R_1}{2\pi}K_{vco}=a_1*\frac{3}{8}\frac{I_{CP}R_1K_{vco}}{N_{eff}}$

a1表示基波的系数

对于由双模分频器的4模运算产生的锯齿波形，a1的值设置为 $2/\pi$ 。

调制频率为fref/4

简单起见，忽略并联电容器C2，首先考虑二阶PLL，杂散电平：

$P_{spur}=20log(\frac{\Delta f_{pk}}{2f_m})=20log(a_1\frac{3}{4}\frac{I_{CP}R_1K_{vco}}{f_{ref}N_{eff}})=-16.4[dBc]$

对于过阻尼回路，上述等式也可以表示为

$P_{spur} \approx 20log(3\frac{f_{BW}}{f_{ref}})$

环路带宽近似为： $f_{BW} \approx \frac{I_{CP}R_1 K_{vco}}{2\pi N_{eff}}$

注意，分数杂散电平不取决于给定fBW与fref比值的分频比，因为小数分频是由双模分频器完成的，双模分频器吞下的脉冲的周期与VCO的周期相同。

考虑一个三阶PLL，包括图中C2，杂散电平变为

$\begin{aligned} P_{spur} &= 20log(a_1\frac{3}{4}\frac{I_{CP}R_1K_{vco}}{f_{ref}N_{eff}})-20log(2\pi\frac{f_{ref}}{4}R_1C_2) \\&=20log(a_1\frac{3}{2}\frac{I_{CP}K_{vco}}{\pi f_{ref}^2N_{eff}C_2}) \end{aligned}$

5 MHz偏移频率下杂散电平：

$P_{spur}=20log(a_1\frac{3}{2}\frac{I_{CP}K_{vco}}{\pi f_{ref}^2}C_2)=-24.2[dBc]$

在三阶PLL中，C2的波形变为三角形，但傅立叶系数a1可以使用 $2/\pi$ 的值。

注意，随着累加器的控制位增加，即频率分辨率更高，高阶极点的分数杂散抑制效果变得更差。

除非去除或抑制分数杂散，否则分数N合成在实际中是无用的。
当使用具有更大位数的累加器以获得更精细的频率分辨率时，杂散水平变得更高。
必须增加额外的电路来抑制小数杂散

2. 减少杂散

2.1 DAC的相位补偿

理论上，分数杂散可以被完全抑制，因为对于分数N PLL中的累加器的给定控制字，每个参考周期的瞬时相位误差的量是可预测的。

降低杂散的一种简单方法是采用数模转换器（DAC），并补偿电压域中的瞬时相位误差，如图所示。

这种方法存在失配和DAC非线性的问题。

请注意，使用鉴频鉴相器（PFD）时，即使采用完美匹配和理想DAC，该方法也无法完全消除小数杂散。

这是因为PFD基于脉宽调制产生相位误差。
用于补偿脉宽调制脉冲的电压或电荷的量可以平衡每个参考周期的电荷量，但不能完全去除电压涟漪。

当采样保持（S/H）PD用于小数N PLL时，基于DAC的补偿方法更有效。
图中的时序图显示，当小数N分频PLL中使用S/H PD时，经过DAC补偿后，周期性杂散可以得到完全抑制。

2.2 DTC的相位补偿

在具有PFD的常规CP-PLL中，DAC在电压域中的相位补偿对于抑制分数杂散不是那么有效。

数字时间转换器（DTC）可以用于时域中的相位补偿。

如图所示为采用基于DTC的相位补偿方法的4模小数N分频PLL。

与补偿电荷泵输出端相位误差的基于DAC的方法不同，相位补偿在分频器之后完成，即在PFD之前完成。
为了适当地补偿频率相关的相位，延迟锁定环（DLL）被用来自适应地控制DTC中的延迟单元。
DLL通过向DTC提供工艺电压温度（PVT）不敏感的控制电压Vctr，起到复制偏置单元的作用。

如果选择4的分数模，则DLL由具有四个延迟单元的压控延迟线（VCDL）组成。

在这种情况下，当DLL被锁定时，VCDL的总延迟变为Tout，使得每个延迟单元的延迟与Tout/4相同。

通过在来自VCDL的多个相位之间执行顺序相位选择，在DTC之后消除了由于调制双模分频器引起的瞬时相位误差。

DLL的带宽应该比PLL的带宽宽得多，这样PLL的环路动态特性就不会受到DLL的影响。

如果在PLL中设计多相位环形VCO，则可以通过使用多个相位来减少DLL的输入频率或延迟单元的数量。

2.3 多相分数N分频

如果环形VCO之类的多相位VCO可用，则可以利用多个相位来实现真正的分数N分频器，而无需相位补偿或调制。

具有固定分频比N的分频器之后是相位选择器

该相位选择器在分频器输出处以固定相位量Tout/4有效地延长时钟周期。

通过依次选择多个相位的相位边沿（从0.1到0.4），选定的相位被锁定到参考时钟，而不会产生瞬时相位误差。

基本工作原理与基于DTC的方法相同，但相位插值量自动调谐到输出频率，因为多个相位直接来自环形VCO。

为了进一步提高频率分辨率，设计了一个相位分频器，以产生比多个相位之间的失配和非线性限制小数N分频PLL性能的相位更多的相位。

在高频下执行无杂散相位选择对于这种架构来说是相当具有挑战性的任务。
该方法的另一个缺点是需要多相位环形VCO。
对于大多数无线应用，频率合成器采用LC VCO来满足相位噪声要求，并且多相位LC VCO的设计实质上增加了硬件成本。

2.4 伪随机调制法

随着小数N分频PLL输出频率的增加，基于DAC或DTC的补偿方法会使小数N分频PLL难以实现高分辨率。

在双模控制中，分数杂散来源于周期性模式，考虑在数字域中抖动模控制。

在分频器的每个输出端，随机数发生器产生一个随机字Pn，
将其与频率字K进行比较
如果Pn小于K，则执行除以N。
如果Pn大于K，则执行除以（N+ 1）。

频率字K确定N和（N+ 1）的平均出现比率，这给出了对分数除法值的有效控制。

与以前的方法，依赖于相位补偿或多相选择在模拟域中，PRM方法可以提供一个非常精细的频率分辨率，而不管输出频率或分频比。

频率分辨率不受模拟电路的失配或非线性的限制，而是由时钟频率和随机数发生器的位数决定的.因此，基于PRM的杂散抑制被认为是一种全数字调制方法。

在基于PRM的分数N分频中，由于双模分频器的随机调制，会产生白噪声抖动。
PLL中的环路滤波器抑制分频器注入的抖动
- 因为PLL对分频器的相位噪声起到低通滤波器的作用。
该方法在载波附近遭受1/f2相位噪声，该相位噪声不能被PLL的环路滤波器抑制。
- 因为由随机比特调制的双模分频器在频域中产生白色噪声
- 从而由于频率到相位转换中的积分因子而在相位域中产生1/f2噪声。

2.5 ΔΣ调制器

当基于PRM的分数N频率合成中的随机数发生器被Δ Σ（ΔΣ）调制器替换时，对于分数N频率合成，

可以获得ΔΣ调制器的随机调制特性
可以获得ΔΣ调制器的噪声整形特性

双模分频器由数字Δ Σ调制器控制，通过过采样对小数频率进行插值。

Δ Σ小数N分频PLL的工作原理类似于1位Δ Σ模数转换器（ADC），
而双模分频器类似于如图所示的1位量化器。

与PRM方法一样，ΔΣ调制器方法的操作基于全数字调制。

因此，可以简单地通过增加数字调制器的比特数来获得更精细的频率分辨率。

理论上，二阶或更高阶Δ Σ调制器不会为直流输入产生固定音调，因此可以实现无杂散的小数N分频频率合成。

得益于ΔΣ调制器的噪声整形特性，它可以像高通滤波器一样将量化噪声推到高频，

因此ΔΣ小数N分频PLL在载波附近不会出现1/f2噪声。

如上所述，基于PRM的小数分频器在频域中产生白色噪声，从而在

对于二阶Δ Σ调制器，，而。因此，

PRM调制	2阶ΔΣ调制
相域 −20 dB/dec的噪声斜率	相域载波附近噪声斜率为+20 dB/dec
	频域中噪声斜率为+40 dB/dec
	载波附近的相位噪声比VCO或电荷泵等其他电路的相位噪声低得多 Δ Σ调制器的噪声整形效应产生的高频相位噪声被PLL的环路滤波器抑制

1.3 多环路混合频率合成

它是20世纪80年代和90年代初噪声最低的信号源发生器之一。

许多现代信号源发生器采用Δ N小数N分频PLL，不仅是为了获得高性能，而且是为了降低成本。

目的	方法
实现0.1Hz的频率分辨率和低噪声	采用具有辅助小数N环的多环PLL来提高PD频率
分数N运算	DAC的相位补偿
良好的杂散性能	采用S/H PD S/H PD对于小数N PLL和整数N PLL分别具有低小数杂散和参考杂散是非常有效的
灵活的频率合成	反馈路径中具有混频器
高频谱纯度	分立元件，非线性和失配效应可以最小化