💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
⛳️赠与读者
👨💻做科研,涉及到一个深在的思想系统,需要科研者逻辑缜密,踏实认真,但是不能只是努力,很多时候借力比努力更重要,然后还要有仰望星空的创新点和启发点。建议读者按目录次序逐一浏览,免得骤然跌入幽暗的迷宫找不到来时的路,它不足为你揭示全部问题的答案,但若能解答你胸中升起的一朵朵疑云,也未尝不会酿成晚霞斑斓的别一番景致,万一它给你带来了一场精神世界的苦雨,那就借机洗刷一下原来存放在那儿的“躺平”上的尘埃吧。
或许,雨过云收,神驰的天地更清朗.......🔎🔎🔎
💥1 概述
摘要:本文对电力系统中的复杂网络分析(CNA)研究进行了综述。此外,本文提出了一种利用复杂网络分析在电力配电网中寻找微电网(MGs)最优位置的新方法。本文所述的最优位置是指能够增强电网韧性、降低功率损耗和线路负荷、改善电压稳定性以及在停电期间为关键负荷供电的位置。用于确定微电网最优位置的标准基于复杂网络理论中的中心性分析、物理学中的质心(COM)概念以及最近开发的可控配送电网(CDG)模型。本文以IEEE 30节点网络作为案例研究。通过使用MATLAB(MathWorks公司,美国马萨诸塞州纳提克)和PowerWorld(PowerWorld公司,美国伊利诺伊州香槟)进行的仿真结果表明,所提出的方法对于微电网的选址具有实用性。
关键词:集中控制;复杂网络分析(CNA);可控配送电网;电网韧性;微电网选址


一、复杂网络分析理论基础
1.1 核心概念与模型
复杂网络由节点(电力系统中的发电站、变电站、负荷点)和边(输电线路、变压器连接)构成,其特征通过以下参数描述:
- 度分布:衡量节点连接密度,电力网络通常呈现异质性(如无标度特性)。
- 小世界效应:实际电网具有短平均路径长度和高聚类系数,表明局部紧密连接与全局高效传输并存。
- 介数中心性:量化节点/边在信息或能量传递中的枢纽作用,高介数元件对电网稳定性影响显著。
1.2 分析方法
- 拓扑结构分析:计算度分布、聚类系数、平均路径长度,揭示电网整体连接模式。
- 中心性分析:通过度中心性(连接数)、接近中心性(信息传播效率)、介数中心性(路径依赖度)识别关键节点。
- 动态模型:结合物理定律(如潮流方程)构建级联故障模型(CFM),模拟攻击或故障传播过程。
二、电力系统复杂网络分析的核心场景
2.1 脆弱性与鲁棒性评估
- 关键节点识别:基于介数中心性发现IEEE30节点中高介数输电线路(如节点1-2、2-5),其失效可能导致大规模级联故障。
- 攻击模拟:通过随机攻击(模拟设备老化)和蓄意攻击(针对高介数节点)评估电网抗毁性,发现电网对后者更敏感。
- 改进策略:增设自治节点(如储能系统)、优化网络拓扑(如增加冗余连接)可提升鲁棒性。
2.2 故障诊断与恢复优化
- 级联故障建模:基于直流潮流模型模拟IEEE30节点故障传播,发现初始故障在介数高的线路(如节点5-7)会引发更严重停电。
- 恢复策略:优先恢复高介数节点(如平衡节点1)可加速系统重构,减少停电损失。
2.3 微电网与可再生能源优化
- 最优布局:结合质心(COM)和受控输送网格(CDG)模型,在IEEE30节点中确定微电网最佳位置(如节点5、13),降低线损10-15%并提升电压稳定性。
- 可再生能源整合:通过复杂网络分析优化风电接入点(如节点13),减少对主干网的冲击并提高能源利用率。
三、IEEE30节点模型的结构特性与实证研究
3.1 系统参数
- 拓扑结构:30节点(6发电机节点、24负荷节点)、41条支路,总负荷283.4 MW,无功126.2 MVar。
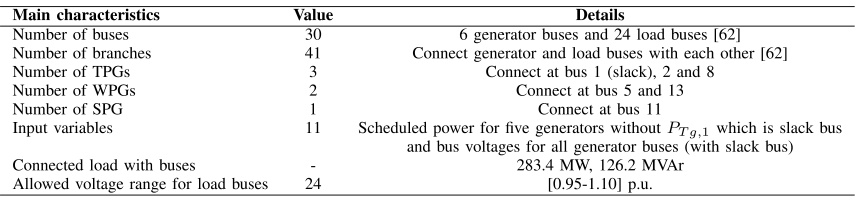
- 关键节点:节点1(平衡节点)、节点2(最大有功输出509.7 MW)为核心电源点;节点5、13为典型负荷中心。
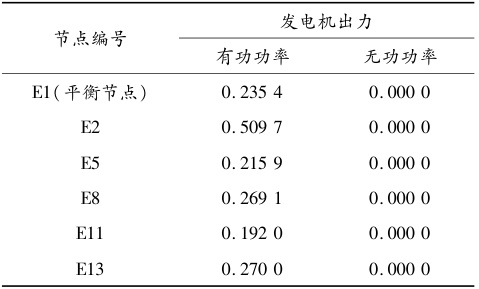
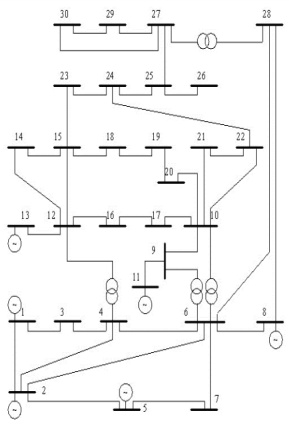
- 电气特性:电压允许范围0.95-1.10 p.u.,变压器分接头调节能力为±10%。
3.2 典型研究案例
案例1:基于介数中心性的脆弱性分析
- 方法:计算线路电抗加权介数,识别高介数线路(如节点2-4、4-6)。
- 结果:蓄意攻击高介数线路导致系统崩溃概率比随机攻击高3倍,验证介数指标的敏感性。
案例2:微电网布局优化
- 方法:结合复杂网络中心性(度、接近度)与COM模型,筛选节点5、13、27作为微电网候选。
- 效果:线损降低12%,关键负荷(如节点8)的供电可靠性提升20%。
案例3:动态级联故障模拟
- 模型:采用DC潮流模型模拟节点5故障,追踪故障传播路径。
- 发现:故障在10秒内扩散至12个节点,验证小世界效应加速级联故障的特性。
四、未来研究方向与挑战
- 多物理场耦合:将信息网(通信节点)与电网(物理节点)结合,研究跨网络级联故障。
- 机器学习融合:利用图神经网络(GNN)预测节点脆弱性,提升评估实时性。
- 高比例可再生能源:研究风光波动对网络拓扑动态性的影响,优化储能配置策略。
五、结论
复杂网络分析为电力系统研究提供了从宏观拓扑到微观动态的全视角工具。以IEEE30节点为代表的模型验证了该方法在脆弱性评估、故障恢复和可再生能源整合中的有效性。未来需进一步结合多学科方法,推动智能电网的鲁棒性与可持续性发展。
📚2 运行结果


部分代码:
%Adds Weights to the graph
G.Edges.Weights = branch_data(:,19);
normz_weights = branch_data(:,17);
lc_weights = line_cap ./max(line_cap);
%plot the graph
Sparse_Graph = plot(G);
saveas(gcf, '../results/Sparse_Graph.png');
%changes the layout from random to circular to resemble small-world phenomenon
layout(Sparse_Graph,'circle'); % This is fig.2 we got in the conference paper, and it is also fig 3 we got in the Journal version
Regular_Graph = plot(G,'Layout','circle'); % This command also show figure 2 also, but I am using it so that I can save the fig as png in the results section on this platform
saveas(gcf, '../results/fig2.png');
%Measures the degree of the nodes
d = centrality(G,'degree'); %The degree of each node
D = mean(d); % the average degree in the whole graph
% All centrality measures in the table at the end of the paper is calculated as follows:
%Mesures the betweenness centrality of nodes and edges
unweigted_betweenness = centrality(G,'betweenness'); % unweigted betweenness
be = centrality(G,'betweenness','Cost',G.Edges.Weights); % weigted betweenness without normalizing the impedence values
weigted_betweenness = centrality(G,'betweenness','Cost',normz_weights); % weigted betweenness with normalizing the impedence values
be_lc = centrality(G,'betweenness','Cost',lc_weights); % weigted betweenness with the line capacities (was not used in the paper)
%Measures the closeness centrality of nodes and edges
unweigted_closeness = centrality(G,'closeness');
weigted_closeness = centrality(G,'closeness','Cost',normz_weights);
%Retrieve the adjacency matrix
A = adjacency(G);
🎉3 参考文献
文章中一些内容引自网络,会注明出处或引用为参考文献,难免有未尽之处,如有不妥,请随时联系删除。(文章内容仅供参考,具体效果以运行结果为准)

🌈4 Matlab代码、数据、文章下载
资料获取,更多粉丝福利,MATLAB|Simulink|Python资源获取
























 393
393

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








