角色动画研究 —— IK的三种结算方法

这篇博客介绍了逆向运动学(Inverse Kinematics, IK)的三种结算方法。

---

背景

IK在角色动画的表现中有着很重要的地位。通常的角色动画都是使用FK(Forward kinematics)来进行计算，这种计算方法中父骨骼的变换与子骨骼的变换决定了子骨骼最终的位置。而IK则相反，IK是先决定子骨骼的变换，然后再推导父骨骼需要由此而产生的变换。

就如同人平时的行为一样——往往是手掌的位置和旋转需要先确定（拍到墙壁上的某个点，抓住某个东西等……）后，再进行手肘变换的计算。这也就意味着IK的结算可能产生未知个数的解（0个或多个……），有可能手掌根本抓不到一个地方，或者手掌到了一个地方手肘可以有多个形态和变换。

和机器人控制论很像……不是吗？其实IK结算在机器人的研究中也有很大的作用。

几何分析

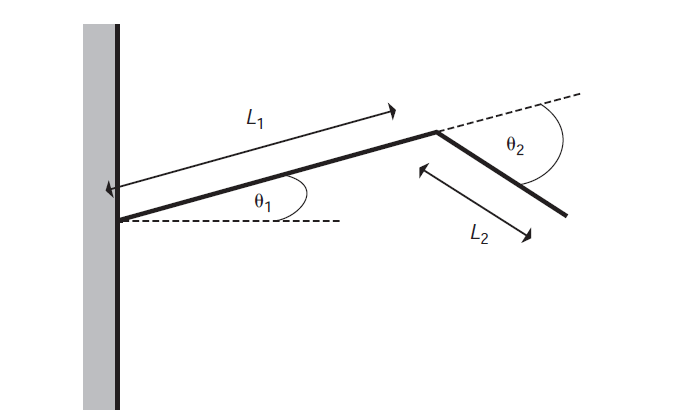
如果说骨骼架构比较简单（例如肩->肘->腕，髋->膝->踝等），那么完全可以通过几何分析来进行IK的结算。

例如手臂上臂长度为$l_1$，下臂长度为$l_2$，再假设每个关节都只有两个旋转自由度，如下图。

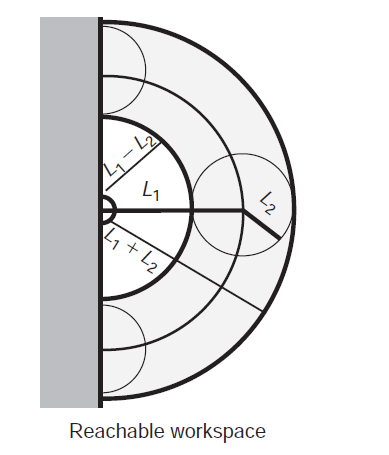
那么最末端的关节便有了一个活动范围(reachable workspace)，当结算IK开始的时候，就需要先确保末端关节在这个活动范围内：

$$|L_1 - L_2| \leq \sqrt{X^2 + Y^2} \leq L_1 + L_2$$

当末端关节的位置确定之后，骨骼架构中对应的两个关节偏转角度$\theta_1$和$\theta_2$就可以通过几何方法确定了。

令尾关节最终位置为$(X, Y)$，连接首关节和尾关节后，可以分析出最终解应该有两个，这两个解关于直线