IMU状态预积分零偏的更新

IMU状态预积分零偏的更新

先前的讨论都假设了在i时刻的IMU零偏恒定不变，当然这都是为了方便后续计算。

然而在实际的图优化中，经常会对状态变量（优化变量）进行更新。那么理论上，如果IMU零偏发生了变化，预积分就应该重新计算，因为预积分的每一步都用到了i时刻的IMU零偏。

但在实际的操作过程中，也可以选用另一种做法：假定预积分观测是随零偏线性变化的，然后在原先的观测量上进行修正。
具体来说，把预积分观测看成$b_{g,i},b_{a,i}$的函数，那么当$b_{g,i},b_{a,i}$更新了$\delta b_{g,i},\delta b_{a,i}$之后，预积分观测应该做如下修正:

于是，问题就变成如何计算上面列写的几个偏导数（雅可比矩阵）。

下面推导这几个雅可比矩阵。核心思想就是将噪声变量移出来求线性化

旋转部分

预积分旋转观测量可以写为：


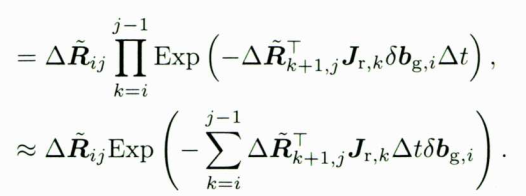
最后一行用到了BCH在$\delta b_{g,i}$为小量时雅克比矩阵接近单位阵的性质。
通过这种方式可以算出$△{\tilde{R}}_{ij}$相对于$\delta b_{g,i}$的雅克比矩阵，记作
$\frac{\partial △{\tilde{R}}_{ij}}{\partial b_{g,i}}$

那么根据上式，可以显式地写出

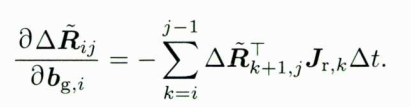
为了方便计算，写出递推的形式

于是得到了如何将这个雅克比矩阵从j-1时刻递推到j时刻。

速度部分

可见，速度相对于零偏的导数可以部分地由旋转导数的结果计算出来。

平移部分

这样就算出了平移对两个零偏变量的雅克比矩阵。

总结

整理上面的雅克比矩阵，得到更整齐的结果

由于后面四种雅克比矩阵本身就是累加的，总结成递推形式