SLAM文献之-Large-Scale LiDAR Consistent Mapping using Hierarchical LiDAR Bundle Adjustment

《Large-Scale LiDAR Consistent Mapping using Hierarchical LiDAR Bundle Adjustment》提出了一种高效且全局一致的激光雷达地图构建方法，结合了层次化的束束调整（Hierarchical Bundle Adjustment, HBA）和位姿图优化（Pose Graph Optimization, PGO），旨在解决传统方法在大规模场景下的计算瓶颈和地图一致性问题。

如图 1

---

算法原理与公式推导

1. 传统方法的局限性

• 位姿图优化（PGO）：通过最小化相邻帧之间的相对位姿误差来优化轨迹，计算效率高，但无法直接优化点云的一致性，可能导致地图局部不一致。

• 激光雷达束束调整（LiDAR BA）：通过最小化点到平面的距离来优化地图一致性，精度高，但在大规模地图中计算复杂度为 $O(N^3)$，难以实时应用。

2. 层次化束束调整（Hierarchical BA）

为解决上述问题，论文提出了层次化的束束调整方法，将整个优化过程分为两个阶段：

a. 自底向上的局部优化

• 构建金字塔结构：将所有帧按照时间顺序划分为多个层级，每一层包含若干帧，形成金字塔结构。
  1、 局部优化结果的抽象与上传
  每层优化后，需要对局部结果进行摘要提取与合并，用于上传到下一层：

  1. 聚合帧位姿与残差分布；

  2. 合并为子图（Submap），形成一个更高层次的节点；

  3. 子图的相对变换（T_sub_i ↔ T_sub_j）再用于上一层优化。

     这种方式形似 “小地图 → 大地图”，支持渐进式构图与优化。

  2、 多层次 BA 框架图示

Layer 3:         [Submap A] — [Submap B] — ...
                    ↑           ↑
Layer 2:         [Cluster A1]  [Cluster B1] ...
                    ↑           ↑
Layer 1:     [Frame_1] [Frame_2] ... [Frame_N]

每一层进行局部 BA，生成更上一层节点间约束。顶层进行全局优化（PGO）。

---

• 局部束束调整：在每一层中，对相邻帧进行局部的束束调整，最小化点到平面的距离误差。

• 优化目标函数：

  $$\underset{{\mathbf{T}}_i}{\min }\sum _{i=1}^N\sum _{j=1}^{M_i}{\left({\mathbf{n}}_{ij}^{\top }({\mathbf{T}}_i{\mathbf{p}}_{ij}-{\mathbf{q}}_{ij})\right)}^2$$

  其中：

  • $\mathbf{T}\_i$：第 $i$ 帧的位姿。

  • $\mathbf{p}\_ij$：第 $i$ 帧中第 $j$ 个点。

  • $\mathbf{q}\_ij$：对应的平面上的点。

  • $\mathbf{n}\_ij$：对应平面的法向量。

通过局部优化，减少了每次优化的问题规模，提高了计算效率。

b. 自顶向下的全局优化

• 构建位姿图：在金字塔的顶层，构建帧之间的位姿图，节点表示帧，边表示帧之间的相对位姿约束。自顶向下的位姿图优化过程旨在减少底层的层次化 BA（Bundle Adjustment）过程中产生的位姿估计误差。底层优化仅考虑了在同一局部窗口中可同时观测到的特征，而忽略了跨不同局部窗口观测到的特征。如图 1 所示，位姿图在金字塔结构中以自顶向下的方式构建。在金字塔的每一层中，图中的因子表示相邻帧之间的相对位姿。具体地，第 $i$ 层中，节点 $x_j^i$ 与 $x_{j+1}^i$ 之间的因子误差项定义为：

$${\mathbf{e}}_{j,j+1}^i=\text{Log}{\left({\left({\mathbf{T}}_{j,j+1}^{i\ast }\right)}^{-1}{\left({\mathbf{T}}_j^i\right)}^{-1}{\mathbf{T}}_{j+1}^i\right)}^{\vee }$$
$$c\left({\mathbf{x}}_j^i,{\mathbf{x}}_{j+1}^i\right)={\left({\mathbf{e}}_{j,j+1}^i\right)}^{\top }{\left({\mathbf{\Omega }}_{j,j+1}^i\right)}^{-1}{\mathbf{e}}_{j,j+1}^i$$
其中，${\mathbf{\Omega }}_{j,j+1}^i$ 是位姿 ${\mathbf{x}}_j^i$ 与 ${\mathbf{x}}_{j+1}^i$ 之间的相关性矩阵（correlation matrix），其中：

• $i\in \mathcal{L}$：表示层级索引集合 L = { 1 , ⋯   , l } \mathcal{L} = \{1, \cdots, l\} L={1,⋯,l}，共 $l$ 层；
• $j\in {\mathcal{F}}^i$：表示第 $i$ 层中节点索引集合 F i = { 0 , ⋯   , N i − 1 } \mathcal{F}^i = \{0, \cdots, N_i - 1\} Fi={0,⋯,Ni​−1}。

该相关性矩阵 ${\mathbf{\Omega }}_{j,j+1}^i$ 是通过自底向上的层次化 BA 优化过程所得到的 Hessian 矩阵 $H$ 的逆计算得出：

$${\mathbf{\Omega }}_{j,j+1}^i={\left({\mathbf{H}}_{j,j+1}^i\right)}^{-1}$$

这表示：底层的局部 BA 为顶层图优化提供了信息矩阵，即顶层的边约束。
由于节点 ${\mathbf{x}}_{j+1}^i$ 与 ${\mathbf{x}}_{s\cdot j}^{i-1}$ 本质上表示同一个节点在不同分辨率层级中的表示，因此可作同一处理。这种结构通常出现在金字塔层次下采样图中，其中 $s$ 是层级缩放因子（如 2 倍下采样）。可以将公式 (4) 中的代价项可以简化为：
$${\mathbf{e}}_{j,j+1}^i=\text{Log}{\left({\left({\mathbf{T}}_{j,j+1}^{i\ast }\right)}^{-1}{\left({\mathbf{T}}_{s^{i-1},j}^1\right)}^{-1}{\mathbf{T}}_{s^{i-1},(j+1)}^1\right)}^{\vee }$$

• ${\mathbf{e}}_{j,j+1}^i$：第 $i$ 层中第 $j$ 与 $j+1$ 个节点之间的误差项。

• ${\mathbf{T}}_{j,j+1}^{i\ast }$：该层中第 $j$ 与 $j+1$ 帧之间的“观测”相对变换（通常来自低层优化结果或IMU等）。

• ${\mathbf{T}}_{s^{i-1},j}^1$、${\mathbf{T}}_{s^{i-1},(j+1)}^1$：从第 $i-1$ 层中根据下采样因子 $s^{i-1}$ 投影出来的第 $j$、$j+1$ 帧的全局位姿。

• $\text{Log}(\cdot {)}^{\vee }$：将变换矩阵转化为李代数形式，即位姿误差向量（例如SE(3)中的6维向量）。
  $$c\left({\mathbf{x}}_{s^{i-1},j}^1,{\mathbf{x}}_{s^{i-1},(j+1)}^1\right)={\left({\mathbf{e}}_{j,j+1}^i\right)}^{\top }{\left({\mathbf{\Omega }}_{j,j+1}^i\right)}^{-1}{\mathbf{e}}_{j,j+1}^i$$

• $c(\cdot ,\cdot )$：第 $i$ 层中两帧之间的优化代价。

• ${\mathbf{\Omega }}_{j,j+1}^i$：误差项的协方差矩阵（或其近似），衡量误差的重要性，通常由下层BA过程的 Hessian 矩阵反转得到。

• ${\left(\cdot \right)}^{\top }\left({\mathbf{\Omega }}^{-1}\right)\left(\cdot \right)$：标准的马氏距离形式，用于加权平方误差。

其中 $i\in \mathcal{L}$，$j\in {\mathcal{F}}^i$，原始位姿图（见图1）被简化为图4所示的形式。需要注意的是，当下采样率 $s<w$（窗口宽度）时，出现在相邻局部窗口重叠区域中的帧可能会贡献多个代价项（每个局部窗口会贡献一个）。因此，最终需要最小化的目标函数为：

$$f(\mathcal{F},\mathcal{X})=\sum _{i\in \mathcal{L}}\sum _{j\in {\mathcal{F}}^i}c\left({\mathbf{x}}_{s^{i-1}\cdot j}^1,{\mathbf{x}}_{s^{i-1}\cdot (j+1)}^1\right)\text{\hspace{1em}(6)}$$

其中， F = { F i 1 ∣ i ∈ F 1 } \mathcal{F} = \{ \mathcal{F}^1_i \mid i \in \mathcal{F}^1 \} F={Fi1​∣i∈F1} 表示第一层中所有帧的集合。最终构建的因子图将通过 GTSAM 中的 Levenberg–Marquardt 方法进行求解。

• 位姿图优化：通过最小化位姿图中边的误差，优化所有帧的位姿，实现全局一致性。原始位姿图（见图1）被简化为图2所示。

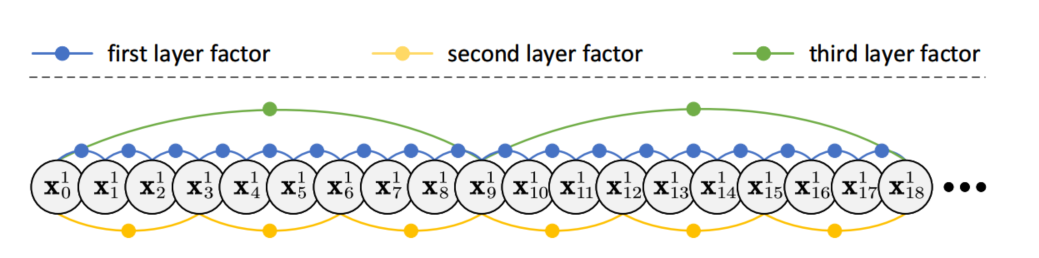
图2

主要创新点

1. 层次化优化框架：将大规模的束束调整问题分解为多个小规模的子问题，结合局部和全局优化，提高了计算效率和地图一致性。

2. 并行处理：局部优化阶段的多个子问题可以并行处理，充分利用多核计算资源，加速了优化过程。

3. 动态窗口策略：在局部优化中，采用动态窗口策略，确保每个窗口内的帧具有足够的重叠区域，提高了优化的稳定性。

4. 鲁棒性增强：通过引入位姿图优化，增强了对错误回环检测和相对位姿估计误差的鲁棒性。

---

实验验证

该方法在多个公开数据集（如 KITTI、MulRan、Newer College）和自采集的固态激光雷达数据上进行了验证，结果表明：([arXiv][1])

• 地图一致性提升：相比传统的位姿图优化方法，生成的地图具有更高的一致性。

• 计算效率提高：在保证精度的前提下，优化时间大幅减少，适用于大规模场景。

• 鲁棒性增强：在存在较大初始位姿误差的情况下，仍能收敛到正确的解。

---

相关资源

• 论文链接：arXiv:2209.11939

• 代码仓库：GitHub - hku-mars/HBA

• 演示视频：YouTube - HBA Demo