点云中点法向量，点拟合的直线，点拟合的平面

Maccy37

已于 2022-12-16 16:34:45 修改

阅读量1.6k

点赞数 1

CC 4.0 BY-SA版权

分类专栏：数学文章标签：线性代数

于 2022-12-16 16:33:51 首次发布

本文链接：https://blog.csdn.net/qq_37611824/article/details/128341199

数学专栏收录该内容

4 篇文章

订阅专栏

本文详细介绍了点云处理中的关键技术，包括如何通过计算点法向量、拟合直线和平面来提取点云特征。文中提供了具体的算法实现过程，并讨论了不同特征提取方法的应用场景。

点云中点法向量

计算步骤：

找到点pi相邻点集合S所有点Vi,然后去中心化,并构造协方差矩阵,公式如下:

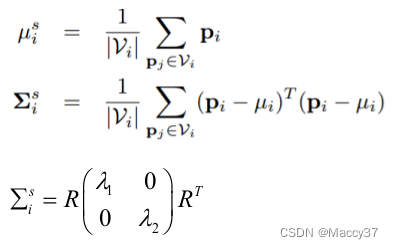
二维点云该点曲率计算方法：

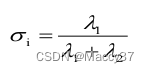
三维点云该点曲率计算方法：

$\frac{\lambda _{1}}{\lambda _{1}+\lambda_{2}+\lambda_{3} }$

最小特征值对应的特征向量就是点的法向量

Eigen::Vector2d ComputeNormal(std::vector<Eigen::Vector2d> &nearPoints)
{
    Eigen::Vector2d normal;

    //计算激光点法向量，NICP计算法向量的方法
    Eigen::Vector2d average;//周围点的几何中心
    average.setZero();//置0
    for(auto v : nearPoints)//遍历每个点
    {
        average += v / nearPoints.size();//求其周围点的几何中心
    }

    Eigen::Matrix2d covariance;//协方差矩阵
    covariance.setZero();//置0
    for(auto v : nearPoints)//遍历每个点
    {
        covariance += (v - average) * (v - average).transpose() / nearPoints.size();//求协方差矩阵
    }

    Eigen::EigenSolver<Eigen::Matrix2d> eigen_solver(covariance);//转化为对角线矩阵
    Eigen::Vector2d eigenValues = eigen_solver.pseudoEigenvalueMatrix().diagonal();//特征值，协方差所有特征值构成向量
    Eigen::Matrix2d eigenVectors = eigen_solver.pseudoEigenvectors();//特征向量，协方差所有特征向量构成矩阵
    normal = eigenValues(0) < eigenValues(1) ? eigenVectors.col(0) : eigenVectors.col(1);//计算法向量

    return normal;
}

点拟合的直线

相邻点集合S拟合成一条直线。

计算步骤：

计算出点集合协方差矩阵M（也就是上面的计算公式），特征向量为E，特征值为V，那么中一个特征值就会明显比其他两个大，最大特征值所对应特征向量就是直线的方向。（特征值：两小一大，大方向）

Eigen::Vector3d ComputeLineNormal(std::vector<Eigen::Vector3d> &nearPoints)
{
    //计算激光点直线法向量
    Eigen::Vector3d center;//周围点的几何中心
    center.setZero();//置0
    for(auto v : nearPoints)//遍历每个点
    {
        center += v / nearPoints.size();//求其周围点的几何中心
    }

    Eigen::Matrix3d covMat;//协方差矩阵
    covMat.setZero();//置0
    for(auto v : nearPoints)//遍历每个点
    {
        Eigen::Matrix<double, 3, 1> tmpZeroMean = v - center;
        covariance += tmpZeroMean * tmpZeroMean.transpose();//求协方差矩阵
    }

    Eigen::SelfAdjointEigenSolver<Eigen::Matrix3d> saes(covMat);
    Eigen::Vector3d unit_direction = saes.eigenvectors().col(2); //最大特征值对应的特征向量->边缘线方向
    // 最大特征值大于次大特征值的3倍认为是线特征
    if (saes.eigenvalues()[2] > 3 * saes.eigenvalues()[1])
    {
        Eigen::Vector3d point_on_line = center;
        Eigen::Vector3d point_a, point_b;
        // 根据拟合出来的线特征方向，以平均点为中心构建两个虚拟点，代替一条直线
        point_a = 0.1 * unit_direction + point_on_line;
        point_b = -0.1 * unit_direction + point_on_line;
    }

    return unit_direction; //返回线的法向量
}

点拟合平面

如果点集合S在一块平面上，

计算步骤：

计算出点集合协方差矩阵M（也就是上面的计算公式），特征向量为E，特征值为V，那么其中一个特征值就会明显比其他两个小，最小特征值所对应特征向量就是平面法向量。（特征值：两大一小，小方向）

//假设传进来的nearPoints有五个点
void  ComputePlaneNormal(std::vector<Eigen::Vector3d> &nearPoints)
{
    //平面方程 Ax + By + Cz + 1 =0 平面法向量(A,B,C)[待求] 已知5个点求解3个未知数，构建超定方程AX = b求解平面法向量;
    Eigen::Matrix<double, 5, 3> matA0; //A = 5 * 3 系数矩阵方程
    Eigen::Matrix<double, 5, 1> matB0 = -1 * Eigen::Matrix<double, 5, 1>::Ones();
    
    for (int j = 0; j < 5; j++)
    {
        matA0(j, 0) = nearPoints[j][0];
        matA0(j, 1) = nearPoints[j][1];
        matA0(j, 2) = nearPoints[j][2];
    }
    Eigen::Vector3d norm = matA0.colPivHouseholderQr().solve(matB0);//平面法向量求解
    double negative_OA_dot_norm = 1 / norm.norm();
    norm.normalize(); //法向量单位化 B.normalize() = B / B.norm() B 是个向量

    // Here n(pa, pb, pc) is unit norm of plane
    bool planeValid = true;
    // 根据求出来的平面方程进行校验，看看是不是符合平面约束
    for (int j = 0; j < 5; j++)
    {
        // if OX * n > 0.2, then plane is not fit well
        //点到平面的距离公式： Ax + By + Cz + D = 0 的距离公式 = fabs(Ax0 + By0 + Cz0 + D) / sqrt(A^2 + B^2 + C^2) 
        //由于前面已经进行归一化，将系数除以分母，所以可以直接代点进去求距离
        if (fabs(norm(0) * nearPoints[j][0] +norm(1) * nearPoints[j][1] + norm(2) * nearPoints[j][2] + negative_OA_dot_norm) > 0.2)
	{
	    planeValid = false;
	    break;
	}
    }
}

参考：点云配准方法---ICP升级版本NICP(Normal ICP) - 古月居

GitHub - HKUST-Aerial-Robotics/A-LOAM: Advanced implementation of LOAM