2 三维空间刚体运动
刚体运动它不光有位置还有自身姿态的变化,一个刚体在三维空间中的运动由旋转和平移组成
2.1 旋转矩阵、变换矩阵
-
点、向量和坐标系
当我们指定三维空间中的某个坐标系,也就是一个线性空间的基 ( e 1 , e 2 , e 3 ) (e_1,e_2,e_3) (e1,e2,e3)时,就可以谈论向量在这组基下的坐标了
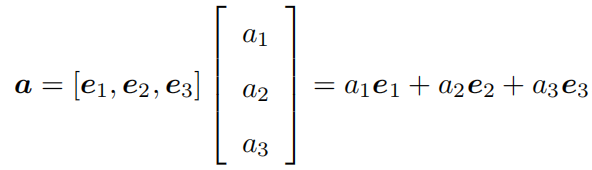
向量的内积,可以描述向量间的投影关系
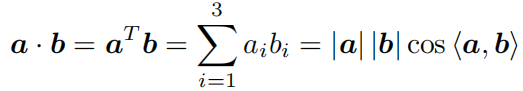
向量的外积,外积的方向垂直于这两个向量,大小为 ∣ a ∣ ∣ b ∣ sin < a , b > |a||b|\sin<a,b> ∣a∣∣b∣sin<a,b> ;引入^ 符号,把外积a × b写成了矩阵
与向量的乘法 a^b,把它变成了线性运算,事实上a是一个反对称矩阵,可以将 ^ 记成一个反对称符号;外积只对三维向量存在定义
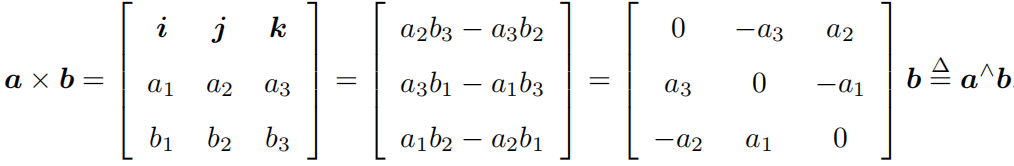
坐标系的选取,给定 x 和 y 轴时,z 就可以通过右手(或左手)法则(四指从x指向y轴,拇指的方向即z轴)由 x × y 定义出来
用外积表示向量的旋转,a 到 b 的旋转可以由向量 w 来描述,如图在右手法则下,大拇指朝向就是旋转向量的方向
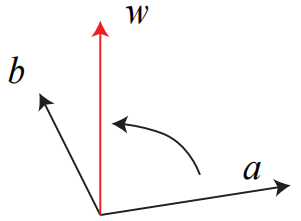
-
坐标系间的欧式变换
在机器人的运动过程中,坐标系之间的变换,常见的做法是设定一个惯性坐标系(或者叫世界坐标系),认为它是固定不动的,相机或机器人则是一个移动坐标系。这个变换关系由坐标系间的变换矩阵 T 来描述。
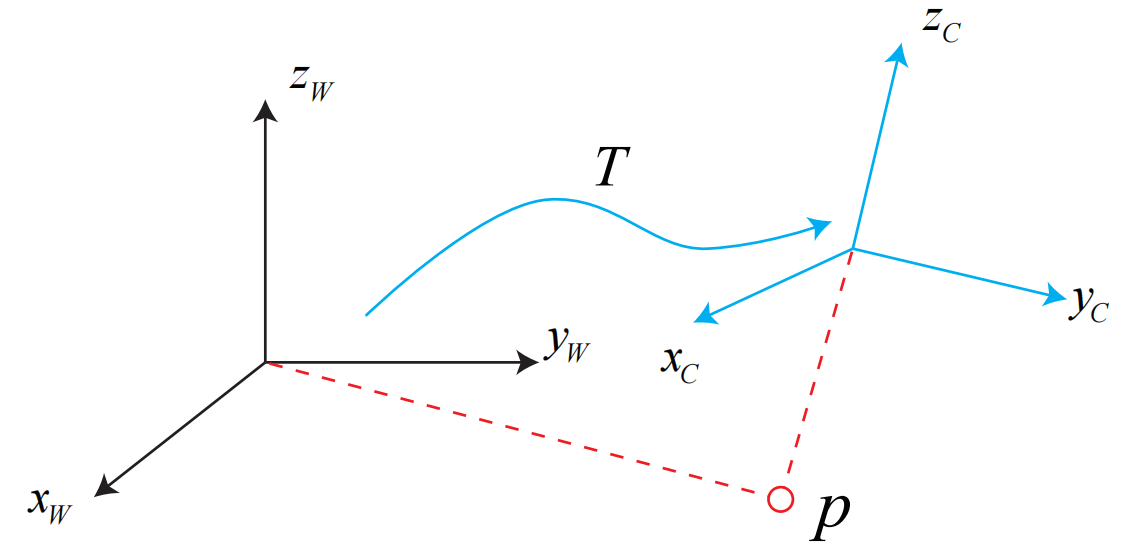
相机运动是刚体运动,它保证了同一个向量在各个坐标系下的长度和夹角都不会发生变化,这种变换称为欧氏变换
在坐标系旋转前后,由同一个向量在前后两个坐标系的坐标有:

矩阵 R 描述了旋转本身,因此它又称为旋转矩阵。旋转矩阵有一些特别的性质,它是一个行列式为 1 的正交矩阵;反之,行列式为 1 的正交矩阵也是一个旋转矩阵。所以,我们可以把旋转矩阵的集合定义如下,SO(n) 是特殊正交群(Special Orthogonal Group)。
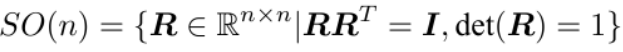
旋转矩阵可以描述相机的旋转,由于旋转矩阵为正交阵,它的逆(即转置)描述了一个相反的旋转。在欧氏变换中,把旋转和平移合到一起,有:
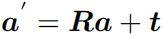
-
变换矩阵与齐次坐标
旋转加平移在变换多次之后会过于复杂

把一个三维向量的末尾添加 1,变成了四维向量,称为齐次坐标。对于这个四维向量,可以把旋转和平移写在一个矩阵里面,使得整个关系变成了线性关系,式中,矩阵 T 称为变换矩阵。
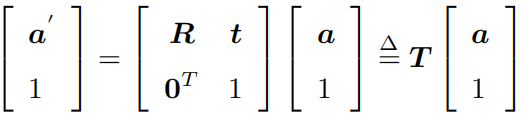
依靠齐次坐标和变换矩阵,两次变换的累加就可以有很好的形式:
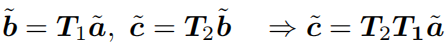
关于变换矩阵 T,它具有比较特别的结构:左上角为旋转矩阵,右侧为平移向量,左下角为 0 向量,右下角为 1。这种矩阵又称为特殊欧氏群(Special Euclidean Group):
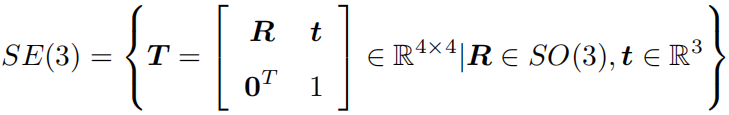
2.2 旋转向量
矩阵表示方式还有些缺点:
- SO(3) 的旋转矩阵有九个量,但一次旋转只有三个自由度,因此这种表达方式是冗余的。同理,变换矩阵用十六个量表达了六自由度的变换。
- 旋转矩阵本身必须是个正交矩阵,且行列式为 1,变换矩阵也是如此。当我们想要估计或优化这个矩阵时,这些约束会使得求解变得更困难。
我们希望有一种方式能够紧凑地描述旋转和平移,对于坐标系的旋转,任意旋转都可以用一个旋转轴和一个旋转角来刻画。于是,可以使用一个向量,其方向与旋转轴一致,而长度等于旋转角,这种向量称为旋转向量,这样只需一个三维向量即可描述旋转。对于变换矩阵,使用一个旋转向量和一个平移向量即可表达一次变换,这时的维数正好是六维。
旋转可以这样表示,那旋转向量和旋转矩阵之间是如何转换的呢?假设有一个旋转轴为 n,角度为 θ 的旋转,它对应的旋转向量为 θn。
-
由旋转向量到旋转矩阵的过程可由罗德里格斯公式(Rodrigues’s Formula )表明,符号 ^是向量到反对称的转换符
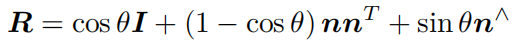
-
从一个旋转矩阵到旋转向量的转换
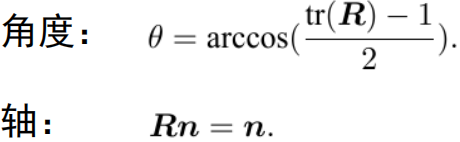
关于转轴 n,旋转轴上的向量在旋转后不发生改变,转轴 n 是矩阵 R 对应特征值 1 的特征向量。求解此方程,再归一化,就得到了旋转轴
2.3 欧拉角、四元数
-
欧拉角
旋转矩阵、旋转向量描述的旋转对我们人类是非常不直观的,欧拉角则提供了一种非常直观的方式来描述旋转——它使用了三个分离的转角,把一个旋转分解成三次绕不同轴的旋转。由于分解方式有许多种,所以欧拉角也存在着不同的定义方法,具体表现为绕XYZ轴旋转的顺序以及每次旋转是绕固定轴旋转的还是绕旋转之后的轴旋转的。
欧拉角中比较常用的一种便是用“偏航-俯仰-滚转”(yaw-pitch-roll)三个角度来描述旋转,它等价于ZYX轴的旋转。
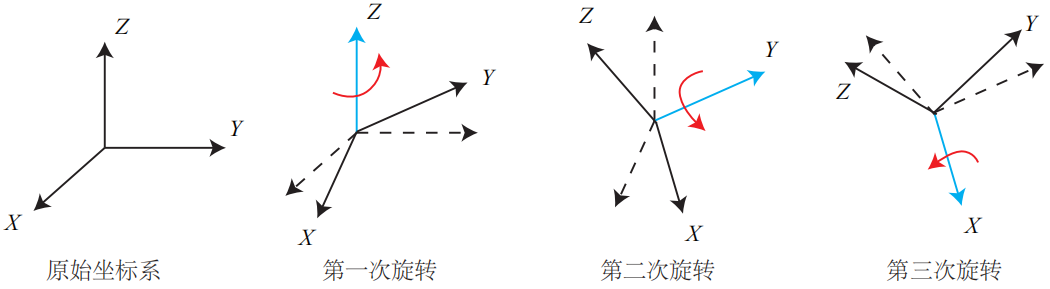
欧拉角的一个大缺点是会碰到万向锁问题(Gimbal Lock),这种形式的欧拉角中,在俯仰角为90°时,第一次旋转与第三次旋转将使用同一个轴,使系统丢失了一个自由度(由三次旋转变成了两次旋转)。这被称为奇异性问题,只要我们想用三个实数来表达三维旋转时,都会不可避免地碰到奇异性问题。我们很少在SLAM程序中直接使用欧拉角。
-
四元数
旋转矩阵用九个量描述三自由度的旋转,具有冗余性;欧拉角和旋转向量是紧凑的,但具有奇异性。而四元数既是紧凑的,也没有奇异性,它是一种扩展的复数。不过四元数不够直观,其运算稍为复杂一些。
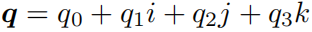
四元数的三个虚部满足关系式:
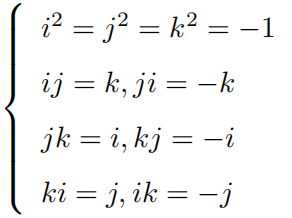
有时也用一个标量和一个向量来表达四元数:
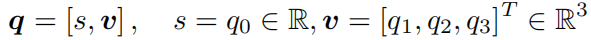
-
四元数与旋转向量的关系
假设某个旋转是绕单位向量 n = [ n x , n y , n z ] T n=[n_x,n_y,n_z]^T n=[nx,ny,nz]T进行了角度为 θ \theta θ 的旋转,那么这个旋转的四元数形式为:
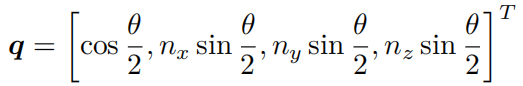
可从单位四元数中计算出对应转角与旋转轴:
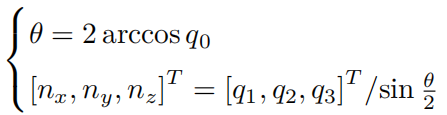
θ 加上 2π得到一个相同的旋转,但此时对应的四元数变成了 −q。因此,在四元数中,任意的旋转都可以由两个互为相反数的四元数表示。同理,取 θ 为 0,则得到一个没有任何旋转的实四元数:
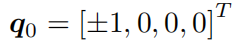
-
四元数与旋转矩阵的关系
把四元数转换为矩阵可以先把四元数 q 转换为轴角 θ 和 n,然后再根据罗德里格斯公式转换为矩阵,不过那样要计算一个 arccos 函数,代价较大。通过一定的技巧绕过这个计算直接给出四元数到旋转矩阵的转换方式:
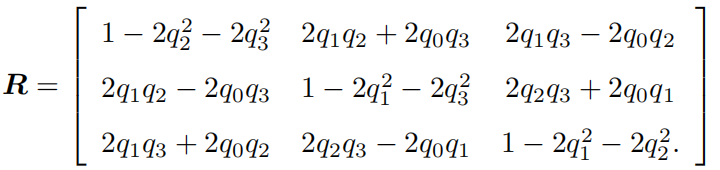
假设矩阵为 R = m i j , i , j {m_{ij}},i,j mij,i,j∈ [1,2,3],其对应的四元数 q 由下式给出:
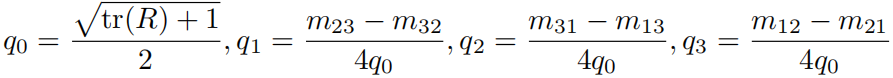
由于 q 和 −q 表示同一个旋转,事实上一个 R 对应的四元数表示并不是惟一的。同时,除了上面给出的转换方式之外,还存在其他几种计算方法。实际编程中,当 q 0 q_0 q0 接近 0 时,其余三个分量会非常大,导致解不稳定,此时我们再考虑使用其他的方式进行转换。
-
用四元数表示旋转
假设空间三维点 p = [x, y, z] ,以及一个由轴角 n, θ 指定的旋转,三维点 p 经过旋转之后变成为 p′,用四元数描述旋转,它们的关系如何来表达呢?
先把三维空间点用一个虚四元数来描述:
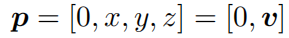
用四元数 q 表示这个旋转:
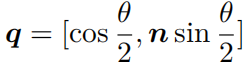
旋转后的点 p′ 可表示为这样的乘积:
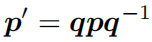
最后,无论是四元数、旋转矩阵还是轴角,它们都可以用来描述同一个旋转。我们应该在实际中选择对我们最为方便的形式。
-
2.4 相似、仿射、射影变换
三维空间中的变换,除了欧氏变换之外,还存在其余几种,其中欧氏变换是最简单的。欧氏变换保持了向量的长度和夹角,相当于我们把一个刚体原封不动地进行了移动或旋转,不改变它自身的样子。而其他几种变换则会改变它的外形。它们都拥有类似的矩阵表示。
-
相似变换
相似变换比欧氏变换多了一个自由度,旋转部分多了一个缩放因子 s,它允许物体进行均匀的缩放。
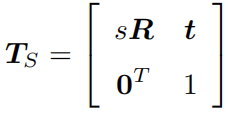
-
仿射变换
与欧氏变换不同的是,仿射变换只要求 A 是一个可逆矩阵,而不必是正交矩阵。仿射变换也叫正交投影。经过仿射变换之后,立方体就不再是方的了,但是各个面仍然是平行四边形。
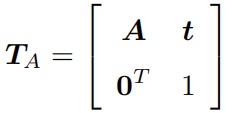
-
射影变换
从真实世界到相机照片的变换可以看成一个射影变换,射影变换是现在讲过的变换中,形式最为一般的。它矩阵左上角为可逆矩阵 A,右上为平移 t,左下为缩放。当 v v v 不为0时,我们可以对整个矩阵除以 v v v 得到一个右下角为 1 的矩阵;否则,则得到右下角为 0 的矩阵。因此,2D 的射影变换一共有 8 个自由度,3D 则共有 15 个自由度。
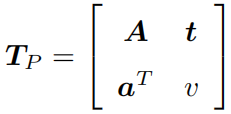






















 568
568











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








