函数表
rot2()%旋转矩阵
det()%矩阵的模
syms %定义变量
simplify() %简述
logm() %矩阵对数
expm() %矩阵指数
skew() %构造反对称指数
vex() %skew()的逆运算
transl2()%二维平移
trot2()%二维旋转
SE2() %齐次变换
axis() %绘制坐标
plotvol()%绘制坐标
trplot2() %绘制二维齐次变换
P=[] %定义一个点
plot_point() %加入图中
inv()%矩阵求逆
double(inv())*[P;1] %求点相对于坐标系的坐标
h2e() %e2h将欧几里得点转换为齐次坐标形式,h2e进行逆转换
homtrans(T,P) %将齐次变换T应用于按列存储在P中的点
eye() %单位矩阵
Twist() %Twist就是Twist
tw.T()%将Twist tw转为SE()
tw.pole%求Twist tw的旋转中心点
rotx() %以x为转轴的旋转矩阵
trplot() %绘制相应的三维坐标系
tranimate() %旋转动画
eul2r() %ZYZ欧拉角表示的旋转矩阵
tr2eul() %找到给定矩阵的欧拉角
rpy2r() %RPY角表示的旋转矩阵
tr2rpy() %找到给定矩阵的rpy角
oa2r() %利用双向量表示法定义坐标系
tr2angvec() %由旋转矩阵定义旋转的角度大小和绕其旋转的向量
eig() %求矩阵的特征值和特征向量
angvec2r() %从角度和向量计算出相应的旋转矩阵
trlog() %分别返回旋转轴和旋转角
UnitQuaternion() %单位四元数
q.norm %四元数的大小
q*q %四元数的乘法
q.inv() %求四元数的共轭
q.R %四元数转化为一个正交旋转矩阵
q.plot() %绘制一个四元数所指的方向
trotx()%绕x轴旋转()的齐次变换矩阵
t2r() %提取旋转部分
transl() %提取平移部分
trnorm()%规范化二维
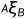 {B}相对于A的相对位姿/对{A}施加平移和旋转使它转化为{B}
{B}相对于A的相对位姿/对{A}施加平移和旋转使它转化为{B}
2.1标准正交旋转矩阵
>> R = rot2(0.2) %弧度为2的旋转矩阵
>> det(R) %矩阵的模
>> det(R*R) %相乘后模仍为1
ans =
1
>> syms theta %工具箱支持符号变量
>> R = rot2(theta)
>> simplify(R*R) %简明表示
>> simplify(det(R))2.2矩阵指数
>> R = rot2(0.3)
R =
0.9553 -0.2955
0.2955 0.9553
>> skew(2) %构造反对称矩阵
ans =
0 -2
2 0
>> vex(ans) %反对称矩阵的逆运算
ans =
2
%可使用logm和vex找到旋转矩阵的旋转角
>> S = logm(R) %计算矩阵R的对数
S =
0 -0.3000
0.3000 0
>> vex(S) %找到反对称矩阵的元素
ans =
0.3000
>> expm(S) %logm的逆运算 构造标准正交旋转矩阵
ans =
0.9553 -0.2955
0.2955 0.9553
>> R = rot2(0.3);
>> R = expm( skew(0.3) ); %与rot2(0.3)等价由【3B1B笔记】e的矩阵指数——怎么算?为什么?知: ,即R = expm(skew(θ) ),也即
,即R = expm(skew(θ) ),也即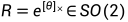
2.3齐次变换矩阵
>> T1=SE2(1,2,30*pi/180)
或>> T1 = transl2(1, 2) * trot2(30, 'deg')
>> axis([0 5 0 5]);
或>> plotvol([0 5 0 5]); %创建2D图并设置边界
>> trplot2(T1, 'frame', '1', 'color', 'b') %绘制齐次变换
>> T2 = transl2(2, 1)
>> trplot2(T2, 'frame', '2', 'color', 'r');
%复合运算的不可交换性
>> T3 = T1*T2
>> trplot2(T3, 'frame', '3', 'color', 'g');
>> T4 = T2*T1;
>> trplot2(T4, 'frame', '4', 'color', 'c');
>> P = [3 ; 2 ]; %定义一个点
>> plot_point(P, 'label', 'P', 'solid', 'ko'); %求在该点相对于坐标系1的坐标
>> P1 = inv(T1) * [P; 1] %对点P附加一个1将欧几里得点转换为齐次形式
>> h2e( inv(T1) * e2h(P) ) % e2h将欧几里得点转换为齐次坐标形式,h2e进行逆转换
>> homtrans( inv(T1),P) %将齐次变换inv(T1)应用于按列存储在P中的点2.4旋转
>> plotvol([-5 4 -1 5]);
>> T0 = eye(3,3);
>> trplot2(T0, 'frame', '0');
>> X = transl2(2, 3);
>> trplot2(X, 'frame', 'X');
>> R = trot2(2);
>> trplot2(R*X, 'framelabel', 'RX', 'color', 'r');
>> trplot2(X*R, 'framelabel', 'XR', 'color', 'r');
>> C = [1 2]';
>> plot_point(C, 'label', ' C', 'solid', 'ko')'
>> RC = transl2(C) * R * transl2(-C)
>> trplot2(RC*X, 'framelabel', 'XC', 'color', 'r');
RX绕原点旋转,而XR绕X点旋转。
而对于绕C旋转的XC,从右向左读,先将C点转换到原点,绕C旋转,然后再将坐标系平移回C
2.5 Twist
>>tw = Twist('R',C)%以R为旋转扭,C为旋转中心点的坐标变换
tw =
( 2 -1; 1 )
>>tw.T(2)%沿twist中心点旋转2弧度的旋转矩阵
ans =
-0.4161 -0.9093 3.2347
0.9093 -0.4161 1.9230
0 0 1.0000
>>tw.pole' %求twist的旋转中心点
ans =
1 2
>>tw = Twist('T', [1 1]) %纯平移的twist
tw =
( 0.70711 0.70711; 0 )
>>tw.T(sqrt(2)) %对纯平移的twist,参数为根2,变换矩阵为
ans =
1 0 1
0 1 1
0 0 1
>> T = transl2(2, 3) * trot2(0.5) %任意坐标变换矩阵
T =
0.8776 -0.4794 2.0000
0.4794 0.8776 3.0000
0 0 1.0000
>>tw = Twist(T) %将SE(2)转为twist,我们注意到C=0.5,即这不是一个单位twist
tw =
( 2.7082 2.4372; 0.5 )
>> tw.T %所以将其转换为一个二维坐标变换时不需要提供旋转角度这个参数
ans =
0.8776 -0.4794 2.0000
0.4794 0.8776 3.0000
0 0 1.0000二维twist的中心思想即为:任何坐标变换均为绕某点的旋转?
三维
欧拉角:ZYZ序列 eul2r
横滚-俯仰-偏航角(卡尔丹角/泰特-布莱恩角/导航角): XYZ序列 rpy2r
双向量表示法: 接近向量 oa2r
3.1正交旋转矩阵
>> R = rotx(pi/2) %以x为转轴的旋转矩阵
>> trplot(R)
>> tranimate(R) %旋转动画
>> R = rotx(pi/2) * roty(pi/2)
>> roty(pi/2)*rotx(pi/2) %证明旋转的不可交换性3.2三角度表示法
>> R = rotz(0.1) * roty(0.2) * rotz(0.3);
>> R = eul2r(0.1, 0.2, 0.3) %计算欧拉角为(0.1, 0.2, 0.3)的等价旋转矩阵
>> gamma = tr2eul(R) %找到给定矩阵的欧拉角
>> R = eul2r(0.1 , -0.2, 0.3) %但如果θ为复数时
>> tr2eul(R) %其反函数结果与原来不同
ans =
-3.0416 0.2000 -2.8416
>> eul2r(ans) %但旋转矩阵相同
>> R = eul2r(0.1, 0, 0.3)
>> tr2eul(R) %对于θ=0的情况,与奇异点有关
>> R = rpy2r(0.1, 0.2, 0.3) %计算RPY角为(0.1, 0.2, 0.3)的等价旋转矩阵
>> gamma = tr2rpy(R) %找到给定矩阵的RPY角3.3双向量表示法
>> a = [1 0 0]'; %接近向量
>> o = [0 1 0]'; %姿态向量
>> R = oa2r(o, a) %利用双向量表示法定义坐标系3.4绕任意向量旋转
>> R = rpy2r(0.1 , 0.2, 0.3);
>> [theta, v] = tr2angvec(R) %由R定义旋转的角度大小和绕其旋转的向量
theta =
0.3655
v =
0.1886 0.5834 0.7900
>> [x,e] = eig(R) %求矩阵的特征值和特征向量
x =
0.6944 + 0.0000i 0.6944 + 0.0000i 0.1886 + 0.0000i
-0.0792 - 0.5688i -0.0792 + 0.5688i 0.5834 + 0.0000i
-0.1073 + 0.4200i -0.1073 - 0.4200i 0.7900 + 0.0000i
e =
0.9339 + 0.3574i 0.0000 + 0.0000i 0.0000 + 0.0000i
0.0000 + 0.0000i 0.9339 - 0.3574i 0.0000 + 0.0000i
0.0000 + 0.0000i 0.0000 + 0.0000i 1.0000 + 0.0000i
>> R = angvec2r(pi/2, [1 0 0]) %从角度和向量计算出相应的旋转矩阵一个正交旋转矩阵总有一个实特征值=1,其相应的特征向量位于矩阵v中对应的列向量,这个向量就是旋转轴
3.5矩阵指数
>> R = rotx(0.3)
>> S = logm(R)
>> vex(S)'
ans =
0.3000 0 0
>> [th,w] = trlog(R) %返回R的旋转角度和旋转轴
th =
0.3000
w =
1.0000
0
0
>> expm(S)
ans =
1.0000 0 0
0 0.9553 -0.2955
0 0.2955 0.9553
>> R = rotx(0.3);
>> R = expm( skew([1 0 0]) * 0.3 ); %与rotx(0.3)等价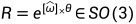 ,其中θ是转角,ω是平行于转轴的单位向量
,其中θ是转角,ω是平行于转轴的单位向量
注:三维斜对称矩阵:

3.6 四元数
Visualizing quaternions, an explorable video series
>> q = UnitQuaternion( rpy2tr(0.1, 0.2, 0.3) ) %构造函数将传递的参数转换为四元数
q =
0.98335 < 0.034271, 0.10602, 0.14357 >
>> q.norm %四元数的大小
ans =
1
>> q = q * q; %四元数的乘法通过重载乘法运算符调用
>> inv(q) %求四元数的共轭
>> q*inv(q)
>> q/q %四元数乘以它的倒数得到单位四元数
ans =
1 < 0, 0, 0 >
>> q.R %四元数转化为一个正交旋转矩阵
>> q.plot() %绘制一个四元数所指的方向
>> q*[1 0 0]' %一个向量可以被一个四元数旋转3.7 4*4齐次变换
%变换的合成
>> T = transl(1, 0, 0) * trotx(pi/2) * transl(0, 1, 0)
%提取旋转部分
>> t2r(T)
%提取平移部分
>> transl(T)'
%规范化
>> R = trnorm(R);区别:3*3标准正交与4*4齐次变换
3.8 Twists
>> tw = Twist('R', [1 0 0], [0 0 0]) %单旋转,ω为1
tw =
( 0 0 0; 1 0 0 )
>> tw.T(0.3)
ans =
1.0000 0 0 0
0 0.9553 -0.2955 0
0 0.2955 0.9553 0
0 0 0 1.0000
>> tw = Twist('T', [0 1 0]) %单平移,ω为0,v为1
tw =
( 0 1 0; 0 0 0 )
>> tw.T(2)
ans =
1 0 0 0
0 1 0 2
0 0 1 0
0 0 0 1
>> X = transl(3, 4, -4);
>> angles = [0:0.3:15];
>> tw = Twist('R', [0 0 1], [2 3 2], 0.5);
>> tranimate( @(theta) tw.T(theta) * X, angles, ...
'length', 0.5, 'retain', 'rgb', 'notext');
>> T = transl(1, 2, 3) * eul2tr(0.3, 0.4, 0.5);
>> tw = Twist(T)
tw =
( 1.1204 1.6446 3.1778; 0.041006 0.4087 0.78907 )
>> tw.pitch
ans =
3.2256
>> tw.theta
ans =
0.8896
>> tw.pole'
ans =
0.0011 0.8473 -0.4389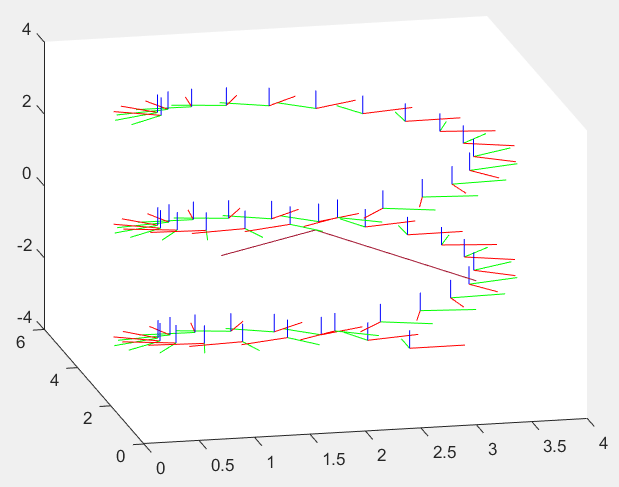
总结

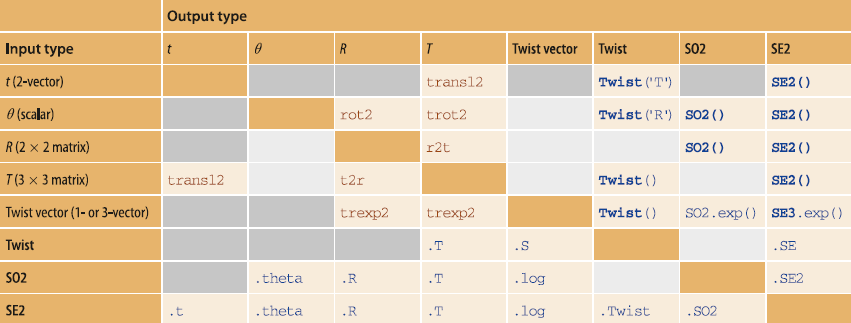

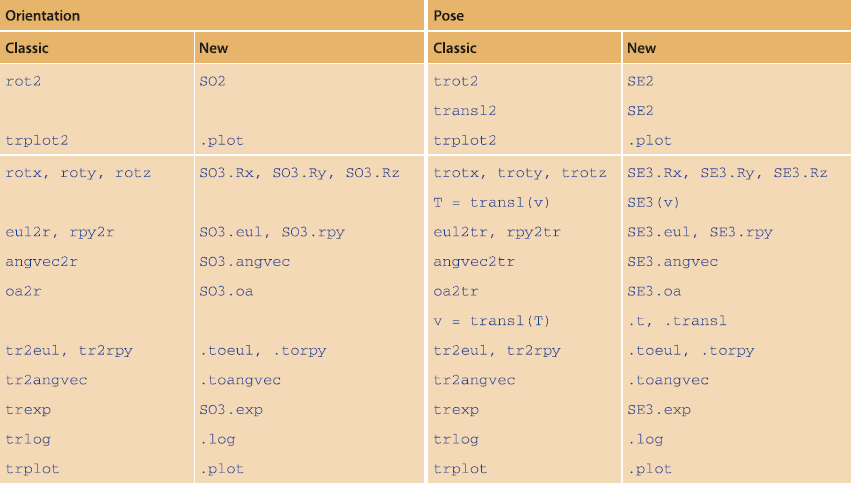
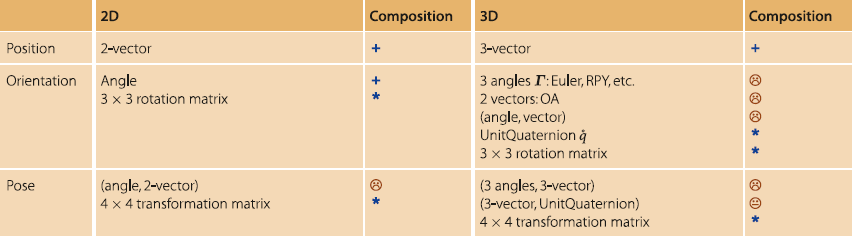






















 3748
3748











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








