自动控制原理学习笔记
自控原理学习笔记专栏
第一章——反馈控制系统的动态模型
第二章——控制系统稳定性分析
第三章——连续时间系统性能分析
第四章——自动控制系统校正与综合
第五章——线性离散系统
线性离散系统
文章目录
1.离散系统
返回目录
系统中有一处或几处信号是脉冲串或数码的系统
离散系统的类型:
-
采样系统:时间离散,数值连续,连续信号某处进行采样
-
数字系统:时间离散,数值量化
A/D过程
-
采样:时间上离散,
-
量化:数值上离散
理想采样过程:
τ ≪ T \tau \ll T τ≪T,认为采样瞬时完成
字长足够,认为 e ∗ ( k T ) = e ( k T ) e^*(kT)=e(kT) e∗(kT)=e(kT)
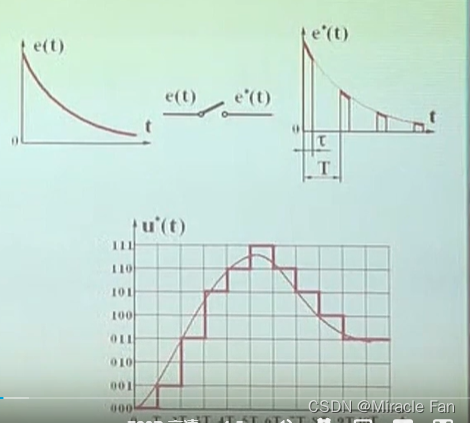
D/A过程
ZOH零阶保持器,将离散信号保持每一拍,得到连续信号

2.信号采样与保持
2.1信号采样
1.理想采样序列
-
因为只在 n T nT nT时刻有效,所有直接使用 e ( n T ) e(nT) e(nT)
-
e ( n T ) e(nT) e(nT)表示采样时的值, δ ( t − n T ) \delta(t-nT) δ(t−nT)代表时间在nT处有效,只在采样点有定义
δ T ( t ) = ∑ n = − ∞ ∞ δ ( t − n T ) e ∗ ( t ) = e ( t ) ⋅ δ T ( t ) = e ( t ) ⋅ ∑ n = 0 ∞ δ ( t − n T ) = ∑ n = 0 ∞ e ( n T ) ⋅ δ ( t − n T ) \begin{aligned} &\delta_T(t)=\sum^{\infty}_{n=-\infty}\delta(t-nT)\\ & e^*(t)=e(t)\cdot\delta_T(t)=e(t) \cdot \sum^{\infty}_{n=0}\delta(t-nT)=\sum^{\infty}_{n=0}e(nT)\cdot \delta(t-nT) \end{aligned} δT(t)=n=−∞∑∞δ(t−nT)e∗(t)=e(t)⋅δT(t)=e(t)⋅n=0∑∞δ(t−nT)=n=0∑∞e(nT)⋅δ(t−nT)
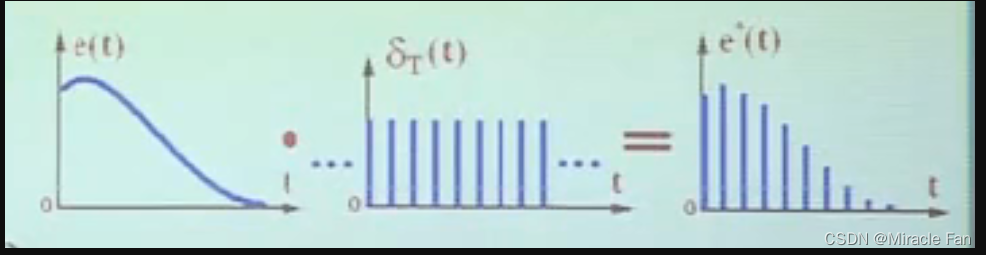
2.Laplace变换
L
:
E
∗
(
s
)
=
L
[
e
∗
(
t
)
]
=
L
[
∑
n
=
0
∞
e
(
n
T
)
⋅
δ
(
t
−
n
T
)
]
=
∑
n
=
0
∞
e
(
n
T
)
⋅
e
−
n
T
s
\begin{aligned} L:E^*(s)&=L[e^*(t)]\\ &=L[\sum^{\infty}_{n=0}e(nT)\cdot\delta(t-nT)]=\sum^{\infty}_{n=0}e(nT)\cdot e^{-nTs} \end{aligned}
L:E∗(s)=L[e∗(t)]=L[n=0∑∞e(nT)⋅δ(t−nT)]=n=0∑∞e(nT)⋅e−nTs
例 : e ( t ) = 1 ( t ) , 求 E ∗ ( s ) E ∗ ( s ) = ∑ n = 0 ∞ 1 ⋅ e − n T s = 1 + e − T s + e − 2 T s + ⋯ = 1 1 − e − T s = e T s e T s − 1 \begin{aligned} 例:e(t) &=1(t), \text { 求 } E^{*}(s) \\ E^{*}(s) &=\sum_{n=0}^{\infty} 1 \cdot e^{-n T s} \\ &=1+e^{-T s}+e^{-2 T s}+\cdots=\frac{1}{1-e^{-T s}}=\frac{e^{T s}}{e^{T s}-1} \end{aligned} 例:e(t)E∗(s)=1(t), 求 E∗(s)=n=0∑∞1⋅e−nTs=1+e−Ts+e−2Ts+⋯=1−e−Ts1=eTs−1eTs
给出 E ∗ ( s ) E^*(s) E∗(s)与 e ( t ) e(t) e(t)在采样点上取值关系,一般可写为封闭形式,用于求 e ∗ ( t ) e^*(t) e∗(t)的z变换或系统的时域响应
3. 傅氏变换 δ T ( t ) = ∑ n = − ∞ ∞ δ ( t − n T ) \delta_T(t)=\sum^{\infty}_{n=-\infty}\delta(t-nT) δT(t)=∑n=−∞∞δ(t−nT)
-
E ∗ ( s ) = 1 T ∑ − n = ∞ ∞ E ( s + j n w s E^*(s)=\frac{1}{T}\sum^{\infty}_{-n=\infty}E(s+jnw_s E∗(s)=T1∑−n=∞∞E(s+jnws), w s w_s ws采样频率
-
一般不可以写成封闭形式,用于 e ∗ ( t ) e^*(t) e∗(t)的频谱分析🎈
δ T ( t ) = ∑ n = ∞ ∞ c n e − j n ω s t d t ω s = 2 π / T c n = 1 T ∫ − T 2 T 2 δ T ( t ) ⋅ e − j n ω s t d t = 1 T ∫ 0 − 0 + δ ( t ) ⋅ 1 ⋅ d t = 1 T δ T ( t ) = 1 T ∑ n = ∞ ∞ e − j n ω s t d t e ∗ ( t ) = e ( t ) ⋅ δ T ( t ) = 1 T e ( t ) ∑ n = 0 ∞ e − j n ω s t = 1 T ∑ n = ∞ ∞ e ( t ) ⋅ e − j n ω s t L [ e ∗ ( t ) ] = L [ 1 T ∑ n = − ∞ ∞ e ( t ) ⋅ e − j n ω s t ] = 1 T ∑ n = − ∞ ∞ E ( s + j n w s ) \begin{aligned} \delta_{T}(t)=&\sum_{n=\infty}^{\infty} c_{n} \mathrm{e}^{-j n \omega_{s} t} d t \\ &\omega_{s}=2 \pi / T \\ &c_{n}=\frac{1}{T} \int_{-\frac{T}{2}}^{\frac{T}{2}} \delta_{T}(t) \cdot \mathrm{e}^{-j n \omega_s t} d t=\frac{1}{T} \int_{0^-}^{0^{+}} \delta(t) \cdot 1 \cdot d t=\frac{1}{T} \\ \delta_{T}(t)=&\frac{1}{T} \sum_{n=\infty}^{\infty} \mathrm{e}^{-j n \omega_s t} d t \\ e^{*}(t)=&e(t) \cdot \delta_{T}(t)=\frac{1}{T} e(t) \sum_{n=0}^{\infty} \mathrm{e}^{-j n \omega_s t}=\frac{1}{T} \sum_{n=\infty}^{\infty} e(t) \cdot \mathrm{e}^{-j n \omega_st} \\ L\left[e^{*}(t)\right]&=L\left[\frac{1}{T} \sum^{\infty}_{n=-\infty} e(t) \cdot \mathrm{e}^{-j n \omega_s t}\right]=\frac{1}{T}\sum^ \infty_{n=-\infty}E(s+jnw_s) \end{aligned} δT(t)=δT(t)=e∗(t)=L[e∗(t)]n=∞∑∞cne−jnωstdtωs=2π/Tcn=T1∫−2T2TδT(t)⋅e−jnωstdt=T1∫0−0+δ(t)⋅1⋅dt=T1T1n=∞∑∞e−jnωstdte(t)⋅δT(t)=T1e(t)n=0∑∞e−jnωst=T1n=∞∑∞e(t)⋅e−jnωst=L[T1n=−∞∑∞e(t)⋅e−jnωst]=T1n=−∞∑∞E(s+jnws)

2.2采样定理(Shannon)
信号完全复现的必要条件
w s = 2 π T > 2 w h w_s=\frac{2\pi}{T}>2w_h ws=T2π>2wh, w s w_s ws为采样频率, w h w_h wh为频谱最大宽度
频谱-信号按频率按分解后的表达式
频率特性对系统而言,频谱对信号而言

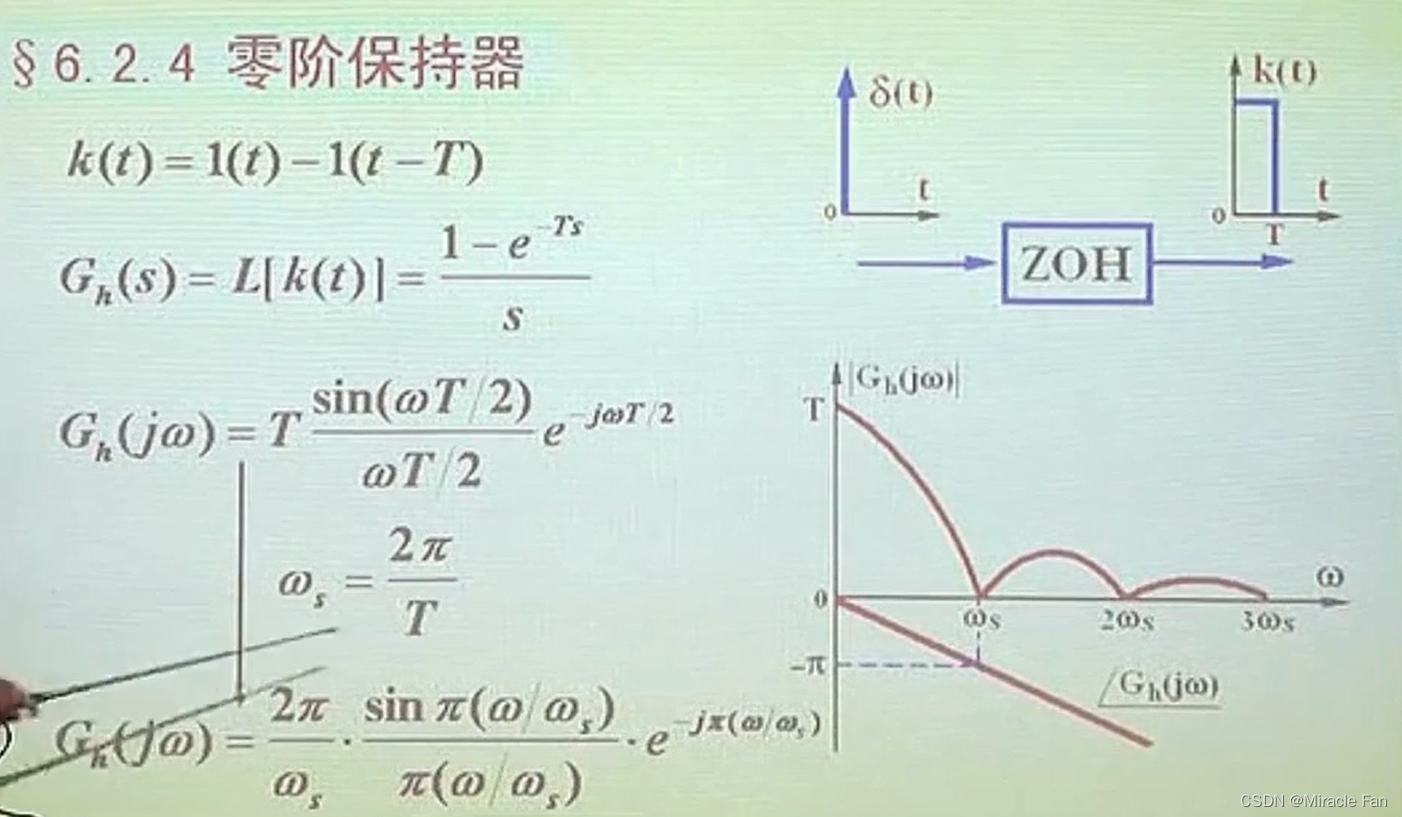
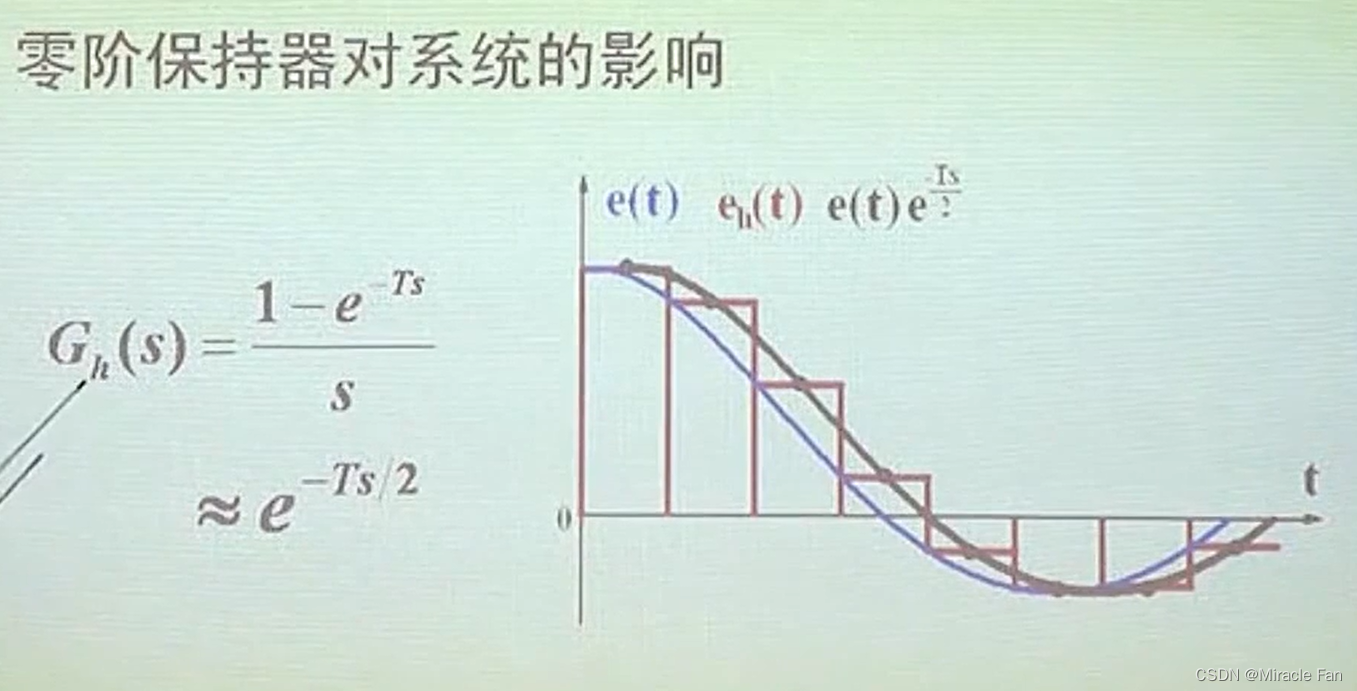
2.3 零阶保持器ZOH
加入零阶保持器可以看成在连续环节的基础上加了一个 T s 2 \frac{Ts}{2} 2Ts纯延时环节
3. Z变换
3.1 定义
对于采样信号的Laplace变换,令
z
−
1
=
e
−
T
s
z^{-1}={e}^{-T s}
z−1=e−Tsd
E
(
z
)
=
Z
[
e
∗
(
t
)
]
=
E
∗
(
s
)
z
=
e
T
s
=
∑
n
=
0
∞
e
(
n
T
)
⋅
z
−
n
E(z)=Z\left[e^{*}(t)\right]=E^{*}(s){ }_{z=e^{Ts}}=\sum_{n=0}^{\infty} e(nT) \cdot z^{-n}
E(z)=Z[e∗(t)]=E∗(s)z=eTs=n=0∑∞e(nT)⋅z−n
{ e ∗ ( t ) = ∑ n = 0 ∞ e ( n T ) ⋅ δ ( t − n T ) E ∗ ( s ) = ∑ n = 0 ∞ e ( n T ) ⋅ e − n T s E ( z ) = ∑ n = 0 ∞ e ( n T ) ⋅ z − n \left\{\begin{array}{l} e^{*}(t)=\sum_{n=0}^{\infty} e(n T) \cdot \delta(t-n T) \\ E^{*}(s)=\sum_{n=0}^{\infty} e(n T) \cdot \mathrm{e}^{-n T s} \\ E(z)=\sum_{n=0}^{\infty} e(n T) \cdot \mathrm{z}^{\mathrm{-n}} \end{array}\right. ⎩⎨⎧e∗(t)=∑n=0∞e(nT)⋅δ(t−nT)E∗(s)=∑n=0∞e(nT)⋅e−nTsE(z)=∑n=0∞e(nT)⋅z−n
-
E(z)只对应唯一的 e ∗ ( t ) e^*(t) e∗(t),不对应唯一的 e ( t ) e(t) e(t)
-
z变换只对离散信号而言
3.2 Z变换方法
- 级数求和法
定义法:
E
(
z
)
=
∑
n
=
0
∞
e
(
n
T
)
⋅
z
−
n
E(z)=\sum^\infty_{n=0}e(nT)\cdot z^{-n}
E(z)=n=0∑∞e(nT)⋅z−n
利用定义的方法求出
E
(
z
)
E(z)
E(z),利用级数的方法
-
部分分式法
-
留数法
E ( z ) = ∑ i = 1 l [ Res E ( s ) z z − e T s ] s = s i E(z)=\sum_{i=1}^{l}\left[\operatorname{Res} E(s) \frac{z}{z-e^{T s}}\right]_{s =s_{i}} E(z)=i=1∑l[ResE(s)z−eTsz]s=si
3.3 Z变换基本定理
复位移定理:
Z
[
e
(
t
)
⋅
e
∓
a
t
]
=
E
(
z
⋅
e
±
a
T
)
Z[e(t)\cdot e^{\mp at}]=E(z\cdot e^{\pm aT})
Z[e(t)⋅e∓at]=E(z⋅e±aT)
初值定理:
lim
n
→
0
e
(
n
T
)
=
lim
z
→
∞
E
(
z
)
\lim_{n\rightarrow0}e(nT)=\lim_{z\rightarrow\infty}E(z)
n→0lime(nT)=z→∞limE(z)
终值定理:
lim
n
→
∞
e
(
n
T
)
=
lim
z
→
1
(
z
−
1
)
⋅
E
(
z
)
\lim_{n\rightarrow\infty}e(nT)=\lim_{z\rightarrow1}(z-1)\cdot E(z)
n→∞lime(nT)=z→1lim(z−1)⋅E(z)
4.Z反变换
4.1长除法
将封闭形式的z域表达式,展开成级数的形式。再通过变换得到时域的表达式

4.2部分分式展开法
注意展开之后是连续的时域信号,需要再进行采样得到采样后的离散信号。

4.3留数法
e ( n T ) = ∑ R e s [ E ( z ) ⋅ z n − 1 ] e(nT)=\sum Res[E(z)\cdot z^{n-1}] e(nT)=∑Res[E(z)⋅zn−1]


5.差分方程
返回目录
前向差分:
Δ
f
(
k
)
=
f
(
k
+
1
)
−
f
(
k
)
Δ
2
f
(
k
)
=
Δ
f
(
k
+
1
)
−
Δ
f
(
k
)
=
f
(
k
+
2
)
−
2
f
(
k
+
1
)
+
f
(
k
)
Δ
3
f
(
k
)
=
Δ
2
f
(
k
+
1
)
−
Δ
2
f
(
k
)
=
f
(
k
+
3
)
−
3
f
(
k
+
2
)
+
3
f
(
k
+
1
)
−
f
(
k
)
Δ
n
f
(
k
)
=
f
(
k
+
n
)
−
n
f
(
k
+
n
−
1
)
+
…
+
(
−
1
)
n
−
1
n
f
(
k
+
1
)
+
(
−
1
)
n
f
(
k
)
\begin{array}{l} \Delta f(k)=f(k+1)-f(k)\\ \Delta^{2} f(k)=\Delta f(k+1)-\Delta f(k)=f(k+2)-2 f(k+1)+f(k) \\ \Delta^{3} f(k)=\Delta^{2} f(k+1)-\Delta^{2} f(k)=f(k+3)-3 f(k+2)+3 f(k+1)-f(k) \\ \Delta^{n} f(k)=f(k+n)-n f(k+n-1)+\ldots+(-1)^{n-1} n f(k+1)+(-1)^{n} f(k) \end{array}
Δf(k)=f(k+1)−f(k)Δ2f(k)=Δf(k+1)−Δf(k)=f(k+2)−2f(k+1)+f(k)Δ3f(k)=Δ2f(k+1)−Δ2f(k)=f(k+3)−3f(k+2)+3f(k+1)−f(k)Δnf(k)=f(k+n)−nf(k+n−1)+…+(−1)n−1nf(k+1)+(−1)nf(k)
后向差分:
∇
f
(
k
)
=
f
(
k
)
−
f
(
k
−
1
)
∇
2
f
(
k
)
=
∇
f
(
k
)
−
∇
f
(
k
−
1
)
=
f
(
k
)
−
2
f
(
k
−
1
)
+
f
(
k
−
2
)
∇
3
f
(
k
)
=
∇
2
f
(
k
)
−
∇
2
f
(
k
−
1
)
=
f
(
k
)
−
3
f
(
k
−
1
)
+
3
f
(
k
−
2
)
−
f
(
k
−
3
)
∇
n
f
(
k
)
=
∇
n
−
1
f
(
k
)
−
∇
n
−
1
f
(
k
−
1
)
\begin{array}{l} \nabla f(k)=f(k)-f(k-1)\\ \nabla^{2} f(k)=\nabla f(k)-\nabla f(k-1)=f(k)-2 f(k-1)+f(k-2) \\ \nabla^{3} f(k)=\nabla^{2} f(k)-\nabla^{2} f(k-1)=f(k)-3 f(k-1)+3 f(k-2)-f(k-3) \\ \nabla^{n} f(k)=\nabla^{n-1} f(k)-\nabla^{n-1} f(k-1) \end{array}
∇f(k)=f(k)−f(k−1)∇2f(k)=∇f(k)−∇f(k−1)=f(k)−2f(k−1)+f(k−2)∇3f(k)=∇2f(k)−∇2f(k−1)=f(k)−3f(k−1)+3f(k−2)−f(k−3)∇nf(k)=∇n−1f(k)−∇n−1f(k−1)
5.1 迭代法
将连续域名的 e ˙ ( t ) \dot{e}(t) e˙(t)用离散域的 e ( k + 1 ) − e ( k ) e(k+1)-e(k) e(k+1)−e(k)代替

5.2 z变换法

6.脉冲传递函数
返回目录
定义:零初始条件下离散系统的输出z变换对输入z变换之比。
-
单位脉冲响应函数的z变换
-
只适用于线性定常离散系统
G ( z ) = C ( z ) R ( z ) G(z)=\frac{C(z)}{R(z)} G(z)=R(z)C(z)
卷积公式: c ( k ) = ∑ i = 0 ∞ g ( k − i ) ⋅ r ( i ) C ( z ) ∑ k = 0 ∞ [ c ( k ) ⋅ z − k ] = ∑ k = 0 ∞ [ ( ∑ i = 0 ∞ g ( k − i ) ⋅ r ( i ) ) ⋅ z − k ] = m = k − i ∑ m = 0 ∞ [ ( ∑ i = 0 ∞ g ( m ) ⋅ r ( i ) ) ⋅ z − ( m + i ) ] = ∑ m = 0 ∞ g ( m ) z − m ∑ i = 0 ∞ r ( i ) z − i = G ( z ) ⋅ R ( z ) G ( z ) = ∑ k = 0 ∞ g ( k ) z − k = C ( z ) R ( z ) \begin{aligned} \mathsf{\text {卷积公式:}} &c(k)=\sum_{i=0}^{\infty} g(k-i) \cdot r(i)\\ &C(z) \sum_{k=0}^{\infty}\left[c(k) \cdot z^{-k}\right]=\sum_{k=0}^{\infty}\left[\left(\sum_{i=0}^{\infty} g(k-i) \cdot r(i)\right) \cdot z^{-k}\right]\\ &\overset{m=k-i}=\sum_{m=0}^{\infty}\left[\left(\sum_{i=0}^{\infty} g(m) \cdot r(i)\right) \cdot z^{-(m+i)}\right]=\sum_{m=0}^{\infty} g(m) z^{-m} \sum_{i=0}^{\infty} r(i) z^{-i}\\ &=G(z) \cdot R(z)\\ G(z)=&\sum_{k=0}^{\infty} g(k) z^{-k}=\frac{C(z)}{R(z)} \end{aligned} 卷积公式:G(z)=c(k)=i=0∑∞g(k−i)⋅r(i)C(z)k=0∑∞[c(k)⋅z−k]=k=0∑∞[(i=0∑∞g(k−i)⋅r(i))⋅z−k]=m=k−im=0∑∞[(i=0∑∞g(m)⋅r(i))⋅z−(m+i)]=m=0∑∞g(m)z−mi=0∑∞r(i)z−i=G(z)⋅R(z)k=0∑∞g(k)z−k=R(z)C(z)
6.1串联环节
含有采样开关,分别求z变换再相乘。没用采样开关,先相乘再进行z变换

6.2 ZOH

G
(
z
)
=
Z
(
1
−
e
−
s
T
s
G
p
(
s
)
)
=
(
1
−
z
−
1
)
Z
(
G
p
(
s
)
s
)
G(z)=Z\left(\frac{1-\mathrm{e}^{-s T}}{s} G_{\mathrm{p}}(s)\right)=\left(1-z^{-1}\right) Z\left(\frac{G_{\mathrm{p}}(s)}{s}\right)
G(z)=Z(s1−e−sTGp(s))=(1−z−1)Z(sGp(s))

求闭环传递函数
对于一般将采样开关放在偏差处时,可以通过如下方式求闭环传递函数。
Φ
(
z
)
=
C
(
z
)
R
(
z
)
=
G
(
z
)
G
(
z
)
H
(
z
)
\Phi(z)=\frac{C(z)}{R(z)}=\frac{G(z)}{G(z)H(z)}
Φ(z)=R(z)C(z)=G(z)H(z)G(z)


plus:能用Mason公式的条件

7.离散系统稳定性分析
7.1基于双线性变换ROUTH判据
令 z = w + 1 w − 1 z=\frac{w+1}{w-1} z=w−1w+1对闭环系统特征多项式进行等效变换,然后利用w域的Routh判据进行判稳。P352

7.2JURY判据
直接根据离散系统闭环特征方程的系数,判别其根是否位于平面上的单位圆内,从而判断是否稳定。
列出Jury步骤:
- 第一行系数是特征方程的系数
- 偶数行系数是奇数行系数的逆序排列
- 其余奇数行计算公式如下:



8.离散系统数字校正
返回目录
对设计控制器还需要满足的约束:
- C ( z ) C(z) C(z)是稳定的:控制器的极点在单位圆内或极点为1
- 控制器是因果的,构成控制器的各项均为当前或过去的数据向
控制器的设计方法:
- 先设计连续控制器,再对控制器进行离散化
- 解析设计法,以最小拍系统设计最为典型
- 直接设计法,有基于z平面的根轨迹法或基于w平面的频域法
8.1典型连续域离散化方法
基本思想:数字控制器与模拟控制器的频率特性等效,将s域的控制器通过各种离散化方法变换到z域,先设计模型控制器,再将其离散化,离散系统响应与连续系统并不一致。
- 一阶差分法:前向差分得到的控制器不能保证控制器本身的稳定,而后向差分离散化的控制器可以保持本身的稳定性
- 脉冲响应法:没有串联型的离散化方法
- 阶跃响应不变法
- 零极点匹配法
- 双线性变换法
8.2 离散化PID校正
- 积分分离数字PID:先用PD……还是会考虑是否加入积分环节
- 不完全微分数字PID:微分作用容易引起高频扰动,在典型PID后面加入一个低通滤波器(一阶惯性环节)来抑制高频扰动
- 微分先行数字PID:为了避免给定值升降给控制系统带来冲击,只对输出反馈量进行微分,不对给定微分
- 变速积分PID:积分分离连续性好,比较平稳
- Bang-Bang PID:根据偏差大小进行选择,当偏差大于阈值,采用Bang-Bang控制,当偏差小于阈值,采用PID
- 带死区的PID:为了防止机构频繁动作,可加入带死区环节
8.3 Smith纯滞后补偿PID
被控对象含有的纯滞后特性经常会引起超调和持续的振荡,会使得系统稳定性下降,严重时可能会失稳。设计PID控制器时不是单独设计的。
8.4Dahlin算法:
期望闭环传递函数:等于对象的纯滞后时间
约束:超调量
针对对象:含纯滞后的一阶、二阶惯性环节(线性系统)
消除振铃现象:离z=-1越远,振铃现象越弱,需要保持静态增益不变。
9.最小拍系统
最小拍系统:典型输入作用下,能在有限拍内结束响应过程且在采样点上无稳态误差。
- 一个系统的冲激响应在最小的有限拍内结束,意味着该系统的稳定度为无穷大。
- 设计的控制器一定要稳定或含有积分
时不变离散系统的闭环传递函数要求包括延迟因子:该延迟因子是应控制器不能含有超前因子要求而设置的,该延迟因子的其中一个来源是被控对象含有纯滞后环节,该延迟因子的其中一个由对象采用ZOH离散化后引入的P376
有纹波和无纹波:
*有纹波:*采样点处稳态误差为0
*无纹波:*采样点和采样点间稳态误差都为0
-
有纹波系统是针对某种典型输入设计的最小拍控制器使输出响应暂态过程在采样时刻点在有限拍后实现无误差
-
有纹波系统之所有纹波主要是控制器输出在有限拍内未与输出同步达到稳定
-
无纹波系统的输出响应与控制器输出同步达到稳定
有纹波与无纹波系统设计步骤:
-
根据典型典型输入信号的z变换积分个数确定m
典型信号 m 1(t) 1 t 2 t 2 / 2 t^2/2 t2/2 3 -
根据被控对象确定延迟拍数h(包括ZOH引入的1拍滞后和源对象固有的纯滞后->看 1 1 − z − 1 \frac{1}{1-z^{-1}} 1−z−11的次数);不稳定的极点个数p,零点个数q®(q为单位圆外、上零点—用于有纹波,r为所有零点—用于无纹波)
-
上述系数可以由m+p个方程求出P377
Φ ( z ) = z − h ∏ i = 1 q ( r ) ( 1 − β i z − 1 ) ( φ 0 + φ 1 z − 1 + ⋯ + φ m + p − 1 z − ( m + p − 1 ) ) \Phi(z)=z^{-h} \prod_{i=1}^{q(r)}\left(1-\beta_{i} z^{-1}\right)\left(\varphi_{0}+\varphi_{1} z^{-1}+\cdots+\varphi_{m+p-1} z^{-(m+p-1)}\right) Φ(z)=z−hi=1∏q(r)(1−βiz−1)(φ0+φ1z−1+⋯+φm+p−1z−(m+p−1))
1 − Φ ( z ) = ( 1 − z − 1 ) m ∏ i = 1 p ( 1 − α i z − 1 ) ( 1 + f 1 z − 1 + ⋯ + f h + q ( r ) − 1 z − ( h + q ( r ) − 1 ) ) 1-\Phi(z)=\left(1-z^{-1}\right)^{m} \prod_{i=1}^{p}\left(1-\alpha_{i} z^{-1}\right)\left(1+f_{1} z^{-1}+\cdots+f_{h+q(r)-1} z^{-(h+q(r)-1)}\right) 1−Φ(z)=(1−z−1)mi=1∏p(1−αiz−1)(1+f1z−1+⋯+fh+q(r)−1z−(h+q(r)−1))
求解所需的方程:
Φ
(
z
)
∣
z
=
1
=
1
,
Φ
′
(
z
)
∣
z
=
1
=
0
,
Φ
′
′
(
z
)
∣
z
=
1
=
0
,
Φ
′
′
′
(
z
)
∣
z
=
1
=
0
,
⋯
,
Φ
(
m
−
1
)
(
z
)
∣
z
=
1
=
0
Φ
(
z
)
∣
z
=
α
1
=
1
,
Φ
(
z
)
∣
z
=
α
2
=
1
,
Φ
(
z
)
∣
z
=
α
3
=
1
,
Φ
(
z
)
∣
z
=
α
4
=
1
,
⋯
,
Φ
(
z
)
∣
z
=
α
p
=
1
\begin{array}{l} \left.\Phi(z)\right|_{z=1}=1,\left.\Phi^{\prime}(z)\right|_{z=1}=0,\left.\Phi^{\prime \prime}(z)\right|_{z=1}=0,\left.\Phi^{\prime \prime \prime}(z)\right|_{z=1}=0, \cdots,\left.\Phi^{(m-1)}(z)\right|_{z=1}=0 \\ \left.\Phi(z)\right|_{z=\alpha_{1}}=1,\left.\Phi(z)\right|_{z=\alpha_{2}}=1,\left.\Phi(z)\right|_{z=\alpha_{3}}=1,\left.\Phi(z)\right|_{z=\alpha_{4}}=1, \cdots,\left.\Phi(z)\right|_{z=\alpha_{p}}=1 \end{array}
Φ(z)∣z=1=1,Φ′(z)∣z=1=0,Φ′′(z)∣z=1=0,Φ′′′(z)∣z=1=0,⋯,Φ(m−1)(z)∣∣z=1=0Φ(z)∣z=α1=1,Φ(z)∣z=α2=1,Φ(z)∣z=α3=1,Φ(z)∣z=α4=1,⋯,Φ(z)∣z=αp=1
控制系统调节时间估计:
t
s
≤
(
h
+
p
+
q
(
r
)
+
m
−
1
)
t_s\le(h+p+q(r)+m-1)
ts≤(h+p+q(r)+m−1)



























 1397
1397

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










