多自由度双质量弹簧振子的自由振动Simulink仿真

写在前面：

这是我研一的第一次课程作业报告，作业完成情况课后与老师沟通了下，也存在比较多小瑕疵，但是由于本人为控制方向，并不是机械方向的，所以也没有继续根据题目要求完善作业内容。但是本仿真总体上完成了确实实现了仿真的总体目的，如果你是一个机械专业的学生，看我做的其实还是很业余的，不过拿来作为一个运用Simulink实现状态空间模型仿真的例子来看其实还是可以的。其他的不足之处我将在文章最后结合我的仿真结果来说明。另外，本作业为原创内容，非抄袭，分享出来与大家交流学习。

1、仿真题目

 

2、代码仿真（未完成实现仿真）

一开始当我看到高维矩阵方程时，我最先想到的就是用Matlab代码求解矩阵方程来进行建模。于是我最先尝试了Matlab的代码仿真，想通过求解高维数的矩阵微分方程直接求解到系统的振动，但是无奈Matlab内置的dsolve函数最大只能求解三维的矩阵，即只能求解到三自由度的自由振动曲线。尝试了很久其他的代码仿真的方式但是都不能完成多自由度下高维矩阵方程的求解。虽然没有做出最后的结果，但也可以作为后面simulink仿真的一个参考，以下为二自由度自由振动系统的仿真代码：

syms t;
[x,y]=dsolve('D2x1+2000*x1-1000*x2=0','2*D2x2-1000*x1+3000*x2=0','x1(0)=0','x2(0)=12','Dx1(0)=0','Dx2(0)=0','t');
t1=0:0.01:2;
x=subs(x,'t',t1);
y=subs(y,'t',t1);

figure;
plot(t1,x,'-');
xlabel('时间/s');
ylabel('位移/m');

hold on;
plot(t1,y,'-');
title('系统响应x(1)和x(2)曲线');
xlabel('时间/s');
ylabel('位移/m');

仿真结果：

而三自由度与二自由度的代码原理一致，代码仿真程序类似，故直接给出仿真结果如下：

 

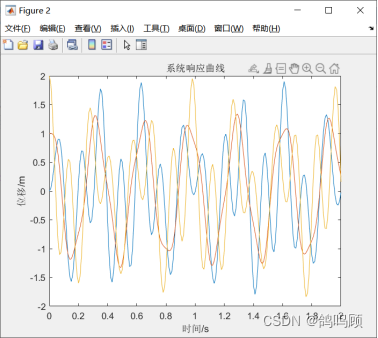
 但是经过与上课展示的实际振子运动模型的分析，我觉得以上代码仿真的结果还是存在着一些问题，归其原因我认为事由于没有设定许多物理条件的限制以及其他初始条件，造成建立的模型并不能完全合理，如弹簧的最大长度，两个振子不能相互交错开等。

3、Simuink仿真

（最大完成了80自由度，好像达到了老师所说的情况，就没再往下做了）

在尝试完代码仿真后，我才发现老师的ppt上写着可以使用Matlab Simulink进行求解，于是我转而尝试使用Simulink进行建模。建模基于多自由度系统的状态空间模型，建立系统的框图，进而可以通过Simulink通过系统框图建立输入输出之间的关系。但是和代码仿真一样，我在建模时还是不清楚模型是否完全正确，只能顺着一条思路往下建模。

首先我从书本最基础的二自由度自由振动系统入手，由系统建模可以得到系统的自由振动方程如下，其中x1和x2分别表示两个振子的位置，x1和x2则表示振子的加速度：

 

由题目的模型，不妨设定以下的初始条件：

x1=1 x2=x1+1=2m1=m=1m2=M=2k1=k2=k3=k=1000

将上述的矩阵方程组拆分开，可以得到二元的微分方程组：

mx1+2kx1-kx2=0Mx2-kx1+2kx2=0

移项构造状态空间方程：

x1=-2kmx1+kx2x2=kMx1-2kMx2=0

带入初始条件，即：

x1=-2000x1+1000x2x2=      500x1-1000x2

根据状态空间方程，即可在Simulink中构建模型框图，进行仿真，模型图如下图所示。另外由于振子存在初始位置，故需要在积分结果为位置的积分环节中设置初始量，带入x1和x2的初始位置分别为1和2，当振子数量继续增多时以1递增。

设置仿真时间为10s，仿真步长设置为1e-5，得到以下的仿真图线：

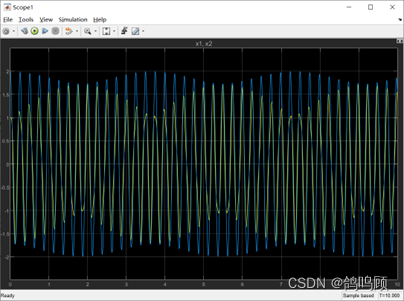
（值得注意的是，我后面通过Simulink建模和代码仿真建模得到的位置曲线并不完全一致，想不到合理的原因，这也让我非常困惑。）

有了以上二自由度模型的基础，我就在它的基础上，手动建立了2阶至10阶的系统模型，过程如下图，并附上10自由度的模型图以及位置信号图线（真的是列出方程之后手动连线搭的，当时还在找规律，所以走线没有整理，看着确实很乱，但是检查过连线和模型都是一一对应的）：

这样的模型图看着非常不整齐，于是我尝试总结了手动搭建前十个自由度的状态空间模型和仿真框图。我先根据最开始二自由度的模型，建立了一个可以很方便拓展的封装子模块，每个子模块分别代表两个自由度的位置信号，以便于建立更多自由度的模块，如下图所示：

其中“500after_in”和下一个模块的“500before_out”相连，最后一个模块则输入0，“1000after_out”和前一个模块的“1000before_in”相连，第一个模块则输入0，“Out1/2”即为信号输出接口。

在该模块的使用下，我也分别用它和前面手动搭建的振动模型的输出结果与封装后的结果进行比对，输出位置曲线均为一致：

 二自由度封装前后的模型

 

四自由度封装前后的模型

为了进一步简化模型，便于更高自由度的仿真，我将五个二自由度的封装模块进一步封装，成为一个可以表示十自由度的封装模型，以下为十自由度封装模块以及建立的十自由度振动模型：

 

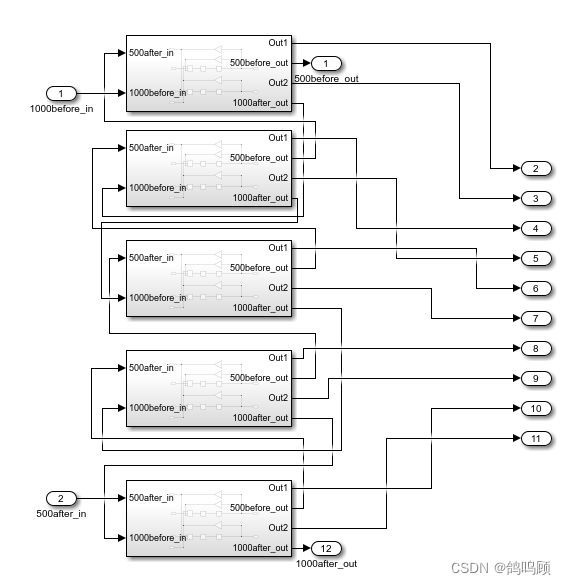
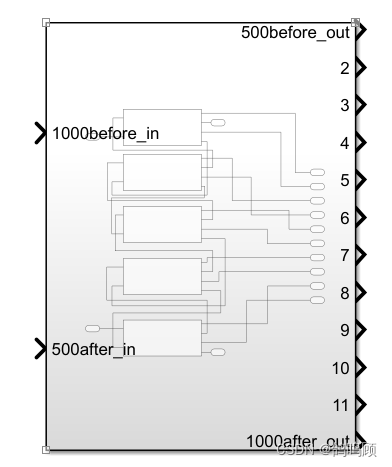
十自由度的封装模块

十自由度封装前后的模型

十自由度下的输出曲线

此时我仍看不出老师所说的那种情况，因此我只能硬着头皮，继续构建更高自由的振动模型。于是我直接一口气，由十自由度封装模型构建出八十自由度的振动仿真模型，框图看着是非常简单，直接相连即可，但是连玩之后每个最基础的二自由度子模块的位置信号初始值都需要手动设置初值，也就是八十自由度的仿真实际上要点进每个自由度设置初值，工作量真不小，希望模型不要搞错了（相比前一个加一）：

由8个十自由度封装模块构成的八十自由度的仿真模型

八十自由度的位置输出曲线较多，为便于更清晰的观察曲线，如上建模图所示，我将分为输出曲线以10个为1组，共得到以下的位置变化曲线：

第1~10个振子位置曲线

 

第11~20个振子位置曲线

第21~30个振子位置曲线

第31~40个振子位置曲线

第41~50个振子位置曲线

第51~60个振子位置曲线

第61~70个振子位置曲线

第71~80个振子位置曲线

写在最后：等到知道了真正正确的数据处理方法之后，我才发现我自己这种愣头青硬怼到80自由度的方式还是挺逗的。回到题目，要求的单位脉冲输入其实我是没有加进去的，我只在每个模块里设置了初值，这是一处bug；此外，我看机械专业其他同学做的，最后的振动响应分析应该是在频域进行的，像我这种位置-时间的时域曲线确实没法很明显的得到正确的波形，正确的响应曲线中，在谐振频率处会出现一个下跌，且随着自由度的增大，下跌幅度会越来越大。这里课上的图线也忘记拍图了。

虽说模型没建错，但是数据处理上还需要进一步完善，如果有同学需要参考我这个做振动响应分析的话，可能需要参考我这再进行进一步的分析，我本人确实本科没接触这些机械相关的知识，都不知道改怎么转换到频域去，专业人士看个乐子就好。

最后感谢你看到这里，我主要还是做电机控制方向的一些东西，如果你嫌麻烦想要文件的话呢，直接私聊我吧，不过我这个写的应该也挺详细了，可以直接照着做。欢迎交流哈！