手把手学电控系列第二篇：FOC控制理论——从根源上解释电流环PI参数如何设计

沉沙丶

已于 2025-04-08 17:02:06 修改

阅读量4.7k

点赞数 48

分类专栏：手把手学电控系列文章标签：电机控制永磁同步电机参数整定电流环 PI调节器

于 2024-11-05 00:04:56 首次发布

本文链接：https://blog.csdn.net/sy243772901/article/details/143486257

版权

手把手学电控系列专栏收录该内容

2 篇文章

订阅专栏

6 电流环调试方法及验证思路（simulink）

7 更换电机如何快速设计参数及调试仿真

小结

前言：

在现代工业自动化和新能源汽车领域，永磁同步电机（Permanent Magnet Synchronous Motor，简称PMSM）以其高效率、高性能和紧凑的结构设计，成为了驱动系统的首选。而在PMSM的高效运行背后，电流环的精确控制无疑是其矢量控制系统中的核心。今天，我们就来一探究竟，了解电流环如何通过PI（比例-积分）控制器，实现对电机电流的快速和准确控制，从而确保电机转矩的精确输出。

矢量控制中电流环重要性高

我们一直挂在嘴边的矢量控制技术，也称为磁场定向控制（Field Oriented Control，FOC）。它通过将电机的三相电流分解为两个正交的分量——直轴（d轴）和交轴（q轴）电流，实现了对电机磁场和转矩的独立控制。这种控制方式不仅提高了电机的动态性能，还优化了其效率和转矩输出，整体控制框图如下图所示。

在这一控制框架下，电流环扮演着至关重要的角色。它负责实时监测和调整电机的电流，确保电机按照预定的控制策略运行。电流环的性能直接影响到电机的响应速度、稳定性以及整体效率。

电流环的基本控制：PI控制器

为了实现电流环的精确控制，工程师们通常采用PI（比例-积分）控制器。这种控制器通过比例（P）环节快速响应电流偏差，而积分（I）环节则用于消除稳态误差，确保电流的长期稳定。PI控制器的这种组合，使得电流环能够在短时间内对电流变化做出反应，同时保持长期的稳定性。当然也存在非常多的其他控制方式，较为基础的分类如下所示：

虽然后续有很多进阶版本的电流环控制策略，但是性能的提升往往伴随着复杂度的提升，PI调节器仍然是”性价比“最高的一种方式。目前本篇文章定位为系列的第二篇，目的为夯实基础与技能巩固，因此本部分专注于对最传统的PI调节器进行分析与验证，后续进阶篇会针对其他电流环策略进行拓展。

电流环的挑战与机遇

尽管PI控制器为电流环提供了强大的控制能力，但在实际应用中，工程师们仍面临着诸多挑战。例如，电机参数的变化、外部负载的扰动以及控制系统的非线性特性，都可能影响到电流环的性能。因此，如何设计和调整PI控制器的参数，以适应不同的工作条件和要求，成为了电机控制领域的一个热点问题。

在这篇文章中，我们将深入探讨电流环的设计原理、PI控制器的参数整定方法，以及在实际应用中如何优化电流环的性能。通过这些内容，我们希望能够为读者提供一个全面的视角，了解电流环在永磁同步电机矢量控制系统中的关键作用，以及如何通过技术创新来提升电机的性能和效率。

1 电机模型

永磁同步电机电流内环的设计，离不开对电压平衡方程的分析。永磁同步电机的电压平衡方程如下所示：

忽略耦合项后，对其进行拉氏变换后可得到电压和电流的传递函数：

2 电流内环结构

基于上面推导的传递函数，电流内环系统结构如下图所示，

除了PI调节器另外两个小惯性环节分别为：

来源于调制模块的近似传递函数；Kpwm/(0.5Ts*s+1)，其中Kpwm在不考虑逆变器非线性等因素的条件下等于1；
来源于DSP/stm32等模块占空比加载延迟一拍；1/(Ts*s+1）

这里的 Ts 较多地方将其描述为采样时间，实际上用开关周期 Tpwm 表述更为合适。当一个载波周期仅进行单次采样时，采样时间Ts = 开关时间 Tpwm，实际上在较多的应用场景中会在一个载波周期内进行多次采样取平均值，这样做能够减少采样噪声的影响。我们后续的分析默认单个周期采样一次，系统传递函数满足上述结构。

当开关频率较高时，可将小惯性环节合并处理，近似后系统的闭环传递函数结构如下所示：

3 开环系统特性分析

在进行闭环PI参数整定之前，对开环特性的分析有助于对闭环系统的理解。在系统不存在任何反馈结构的情况下，系统的开环传递函数为：

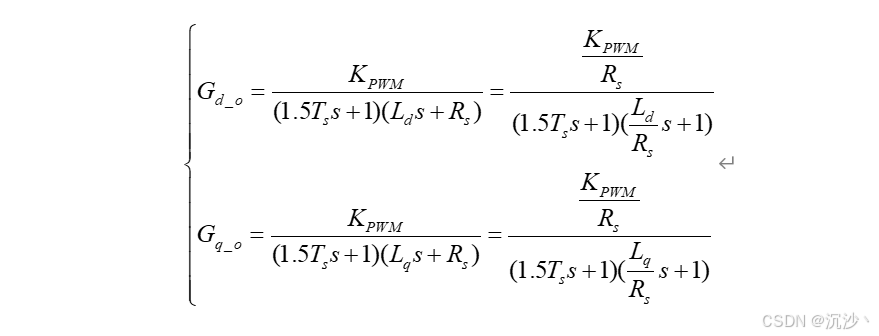
搭建simulink模型进行系统的控制特性分析，仿真如下图所示，利用matlab自带的线性系统特性分析工具，可以较为方便的分析系统特性。

具体的操作：点击 Linearization Management -> 电机 Model linearizer 工具 -> 点击 bode.

系统的伯德图分析如下图所示（此时代入电机参数 Ld = 0.00525，Rs = 0.958）：

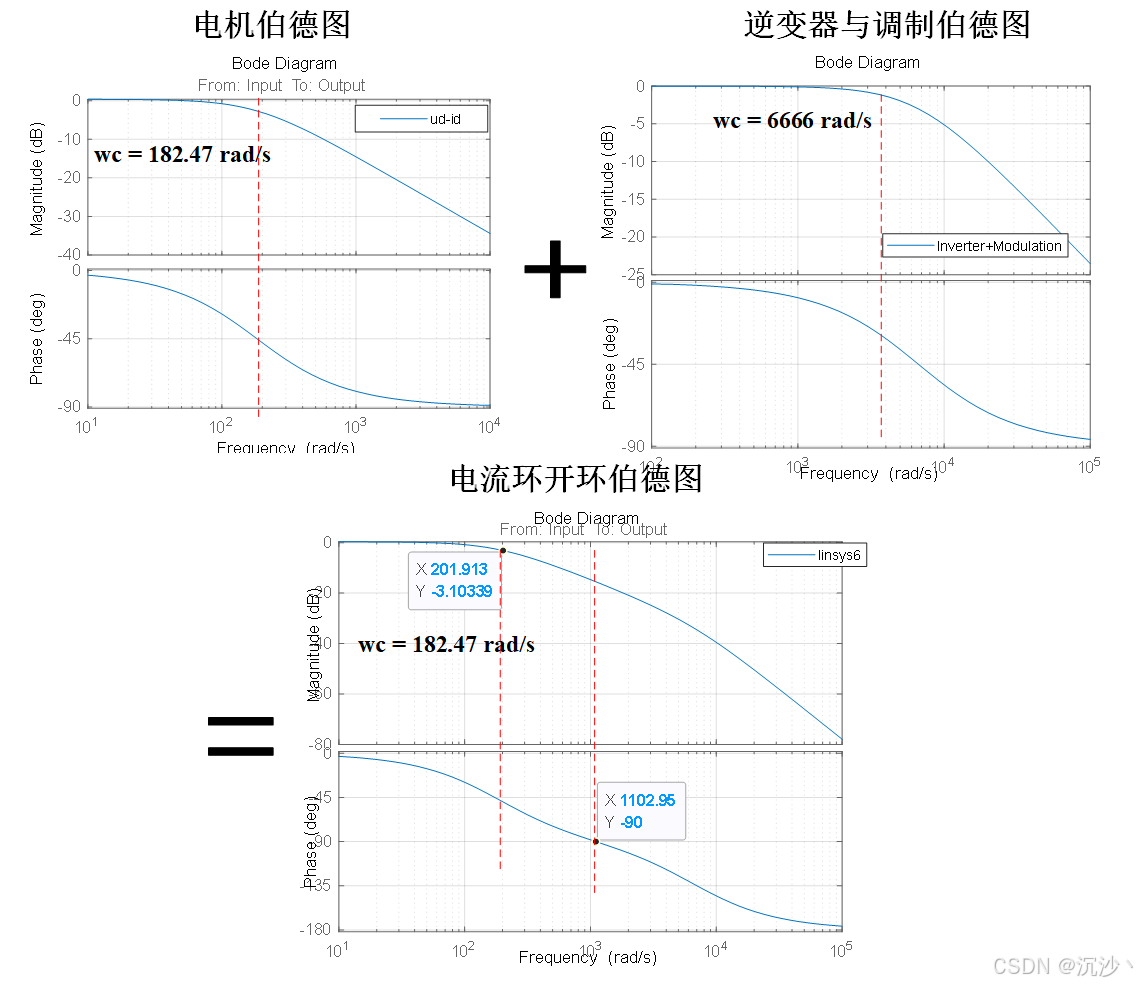
一阶惯性环节相关的基础知识可以查阅博客：一阶惯性环节的性能分析——自动控制原理基础补充（二）-CSDN博客https://blog.csdn.net/sy243772901/article/details/110311114 进一步的，系统开环传递函数的零极点分析也能得到分析，零极点分布如下图所示，系统存在两个极点，一个极点由电机参数决定，实轴大小为 x = - Rs/L；另一个极点由逆变器和调制模块的时间常数决定，其实轴大小为 x = 1/1.5Ts。其中由电机参数决定的极点起到主导作用。

通过以上的bode图和零极点分布图可以得到以下的关键信息：

电机自身的伯德图也类似为一个一阶低通滤波器，其截止频率为 h rad/s(h = Rs/Ldq);
开关频率较高时，逆变器的截止频率也较高；逆变器+调制环节对整体电流环开环伯德图影响较小；

此时对开环传递函数施加一个单位阶跃指令，在0.5s时施加外部扰动-0.5；可以看到系统的响应如下图所示，可以看到系统不仅跟随存在静态误差，在施加外部扰动后也无法收敛到给定。此时的系统性能是较差的。

4 PI参数整定原理及参数计算

电流内环的作用是在电机启动过程中能够以最大电流启动，同时在外部扰动是能够快速恢复，加快动态跟踪响应速度，提高系统的稳定性。依据陈伯时老师的《电力拖动自动控制系统--运动控制系统（第4版）》中阐述的理论，将电流环的开环传递函数整定为一个典型一型环节有利于电机的快速启动依据抗扰动的需求。

典型 I 型环节的开环传递函数如下所示，该典型I型系统存在两个关键参数，即开环增益K以及惯性环节时间常数T。

电机的开环传递函数：

要想将电机的开关传递函数整定成典型I型环节，就必须去除一个分母中的（As+1）的形式，而PI调节器的传递函数为：

实际上这个过程就是用PI 调节器的零点去对消电流内环传递函数中的极点，用零极点对消的方式消除由电机参数决定的那个极点。

具体对消的过程如下所示：

开环增益K以及惯性环节时间常数T可被表示为：

回顾一下陈伯时老师的《电力拖动自动控制原理》书籍中关于工程整定法的章节，一阶系统按 KT = 0.5 时系统性能最佳。最终可以得到PI调节器的参数：

上面是d轴的参数计算公式，q轴的计算公式与此同理，只用将其中的Ld替换成Lq即可。当电机类型为隐极性电机时，dq轴电流环参数一致，只有凸极性电机dq轴电流环参数不一致。

搭建仿真验证，仿真结构框图如下所示：

结果如下图所示，图中黑色为整定PI后闭环跟随的效果，蓝色为开环跟随的效果，可以看到从跟随指令的角度，整定后的电流环具备更快的响应速度，且无静态误差。

下图为抗干扰性能测试，可以看到整定PI后抗扰动效果也明显优于开环效果，开环在施加了0.3的扰动后直接失控了，其输出值一直保持为0。而闭环整定PI后的跟随结果能够在出现跌落后，快速回复到指令值。

5 为什么用开环整定？

在控制系统设计中，我们经常采用开环整定而不是直接整定闭环性能，这背后有着深刻的原因。对于典型的I型系统，开环参数直接影响闭环系统的行为，这一现象是由I型系统固有的结构特性所决定的。有兴趣深入了解的读者可以尝试推导这类系统的闭环传递函数，通过这一过程，可以清晰地观察到开环参数K和T是如何决定闭环系统的阻尼比和自然频率的。这两个参数是闭环性能的决定性因素，它们直接关联到系统的动态响应和稳定性。

系统的结构框图如下所示：

其闭环传递函数如下所示，这是一个二阶系统的标准形式

系统的阻尼比和自然频率为：

对于一个闭环传递函数为二阶时，通常配置阻尼比为0.707，从而得出KT = 0.5为最优参数，这里是其来源。

这里值得一提的是二阶系统的最优阻尼比通常被认为是0.707，这个值是基于对系统瞬态响应和稳态误差之间权衡的结果。以下是为什么0.707是一个常见最优阻尼比的解释：

瞬态响应：阻尼比 ζ 影响系统的瞬态响应。较低的阻尼比会导致较大的超调和振荡，而较高的阻尼比会减少超调但增加系统的上升时间。
调整时间：阻尼比也影响系统的调整时间。对于给定的自然频率 ωn，阻尼比为0.707的系统具有最短的调整时间，这是从瞬态响应的角度来看的。
超调量：对于阻尼比 ζ=0.707ζ=0.707 的系统，超调量大约为4.6%。这是一个可接受的超调量，对于许多应用来说是合适的。
阻尼比和自然频率的关系：阻尼比和自然频率共同决定了系统的瞬态响应。阻尼比为0.707的系统在自然频率和阻尼比之间提供了一个良好的平衡。

简而言之，开环参数的整定之所以重要，是因为它们在I型系统中扮演着塑造闭环性能的关键角色，并且配置起来简单快捷。通过调整开环参数，我们能够间接但有效地控制闭环系统的特性，从而达到预期的控制效果。这种间接控制的方法不仅实用，而且为系统设计提供了灵活性和深度。

6 电流环调试方法及验证思路（simulink）

在完成了理论的梳理后，以及纯传递函数的仿真后，我还是想更具体的结合PMSM电机以及simulink环境完整的验证一下以上理论，这样也能更加便于实操。往往我们学了东西却找不到依托的实物，就会一下陷入虚无的感觉，但是值得庆幸的是电机控制一定不是虚无的，每个细节都是由实物及物理定律支持的。

话不多说，开始搭建电流环仿真，如下图所示，我们去除了速度环，配置了基础的其他模块，包括逆变器模块、PMSM、clark变换、park变换、PI调节器、SVPWM模块，这些模块一起共同组建了电流内环控制系统，我们仅聚焦于下面控制框图中红色部分。

搭建的仿真模型可以发我邮箱我直接发给你们(博客下留言)，仿真模型如下所示：

其中电机参数如下表所示：

根据上文所述的PI参数计算公式可以得到dq轴电流环的PI，为了以更加清晰的例子展现以及对应上单位大小（这个问题之前有同学问过），具体的计算过程如下，

代入模型中，在进行仿真之前有一步是其他地方很少讲到的细节，需要讲电机的输出转矩接入到负载转矩中，如下图所示。这样做的好处有两个：

避免耦合项的影响，此时电机堵转，电角速度为0，满足前文整定参数的假设；
避免电机在电流指令下出现转速跑飞，电流环的测试iq往往会给一个恒值，iq是转矩电流。在这种情况下电机会持续的输出力矩，这意味着电机会持续加速，直至跑飞，进而无法验证控制效果。

仿真结果的图表如下所示。在仿真中，直轴电流（id）的给定信号在0至0.5秒内设定为5安培，而在0.5至1秒内设定为0安培；交轴电流（iq）的给定信号在0至0.5秒内设定为5安培，随后在0.5至1秒内增加至10安培。从图中可以观察到，电流响应能够紧密跟随给定值，且无静态误差，显示出快速的响应速度和基本无超调的特性。

此外，在0.8秒时，我引入了一个外部负载扰动。图表中清晰地显示了电流能够迅速从扰动中恢复至设定值，表明系统具有出色的抗扰动性能。

再一次的：电流环的PI参数调试建议在堵转工况进行。

7 更换电机如何快速设计参数及调试仿真

在我们的实验中，研究对象往往不仅限于单一电机。当电机参数发生变化时，原有的PI控制参数可能不再适用，这就要求我们重新设计参数。为此，我们开发了一个快速设计参数的小工具。该工具基于MATLAB平台，用户只需输入电机参数，即可自动计算出新的PI控制参数。这里主要针对电流环的PI参数进行调整，而不涉及母线电压、开关频率等其他因素的变化。

只需调整电机参数，仿真框架本身无需修改。在电机参数更新后，用户只需将小工具计算出的PI参数输入到调节器中，即可实现参数的快速更新。

举个例子，假如电机参数更改为以下表格所示电机参数：

将该参数代入到仿真中，仿真结果如下所示，图中仿真结果显示更换电机参数后，按照以上公式计算PI参数能够实现电流的快速跟踪，并且系统还具备较好的抗扰性能。

小结

矢量控制与电流环的重要性：电流环在矢量控制中扮演核心角色，负责实时监测和调整电机电流，直接影响电机的响应速度和稳定性。
PI控制器在电流环中的应用：
- PI控制器通过比例环节快速响应电流偏差，积分环节消除稳态误差，实现电流的快速和准确控制。
- 尽管存在更复杂的控制策略，PI控制器因其高性价比而广泛使用。
电机模型与电流内环结构：
- 永磁同步电机的电压平衡方程是电流内环设计的基础。
- 电流内环系统结构包括PI调节器和两个小惯性环节，分别来源于调制模块和DSP/STM32等模块的占空比加载延迟。
开环系统特性分析：
- 开环传递函数的分析有助于理解闭环系统的行为。
- 利用MATLAB的Bode图分析工具，可以直观地分析系统特性。
PI参数整定原理及参数计算：
- 电流内环的设计要求在电机启动过程中能够以最大电流启动，并在外部扰动下快速恢复。
- 依据典型I型环节理论，可以通过开环增益K和惯性环节时间常数T来整定PI调节器参数。
- 开环参数直接影响闭环系统的行为，通过调整开环参数可以间接控制闭环系统的特性。
电流环调试方法及验证思路（Simulink）：
- 通过Simulink环境验证理论，搭建电流环仿真模型，包括逆变器模块、PMSM、Clark变换、Park变换、PI调节器和SVPWM模块。
- 仿真结果表明，整定后的电流环具有快速的响应速度和出色的抗扰动性能。
更换电机参数的快速设计参数及调试仿真：
- 一个基于MATLAB的小工具，用户输入电机参数后，可以自动计算出新的PI控制参数。
- 通过更换电机参数并使用新计算的PI参数，仿真结果显示系统能够实现电流的快速跟踪，并具备良好的抗扰性能。