生成式AI(2):生成式模型简介之自编码器、变分自编码器和生成对抗网络

生成式 AI (Generative AI)正在迅速改变我们与内容创作的互动方式，尤其是在图像生成领域。近年来，扩散模型(Diffusion Models)成为其中的研究热点，其强大的能力体现在图像生成、文本生成图像、超分辨率与图像修复等多个任务中。

1 生成模型概述

生成模型是一类可以生成新的数据实例的模型。它们不同于判别模型，后者的作用是对数据进行分类。

下图展示了图像空间与潜在分布之间的关系。图中的蓝色箭头表示将图像从图像空间映射到一个低维的潜在分布空间，而橙色箭头则表示从潜在分布中生成图像的过程。也就是说，蓝色箭头代表“压缩”过程，橙色箭头代表“生成”过程。

生成模型的核心思想是：我们可以从一个低维的潜在空间（这个空间的分布通常是高斯分布）生成出具有真实感的图像。你可以把潜在空间想象成一个压缩版本的“图像本质特征空间”，它只保留了最关键的信息。而图像空间——即我们看到的 $128\times 128$ 像素图像——其实只是一个高维度表现形式，其背后隐藏的是更低维的结构。所以，图像空间虽然在像素上是高维的，但在语义上是低维流形(low dimensional manifold)。

为了训练这样的生成模型，通常要让模型学会两个过程：第一是如何把图像“压缩”到潜在空间（图像空间到潜在空间的映射）；第二是如何从潜在空间中的一个点“还原”出一张图像（潜在空间到图像空间的映射）。在生成图像时，我们只需要在潜在空间中随机选一个点（比如从一个标准高斯分布中采样），然后通过模型将其映射到图像空间，就能合成出一张新的图像。

目前，已经发展出很多优秀的生成模型来实现这种从潜在空间到图像的映射功能，比如：自编码器(Autoencoders)、变分自编码器(VAEs)和生成对抗网络(GANs)等。

2 自编码器(Autoencoders)

为了训练一个自编码器，我们首先要有一张原始图像 $x$。这张图像会被输入到一个叫做“编码器”的神经网络中，这个编码器记作 $q_{\varphi }$，其中 $\varphi$ 是这个网络的所有参数，比如权重和偏置。

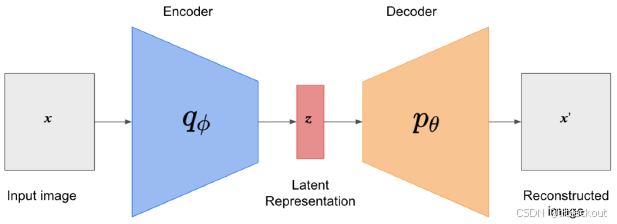
编码器的工作是提取图像中的关键信息，并把原始图像压缩成一个更小、更简洁的表示，这个表示叫做“潜在表示”或“隐藏向量”，用 $z$ 表示。你可以把 $z$ 想象成是这张图像的“核心摘要”——它不包含所有细节，但保留了足以还原图像的关键信息。

接下来，这个潜在表示 $z$ 会被输入到另一个神经网络中，这个网络叫做“解码器”，记作 $p_{\theta }$，其中 $\theta$ 是解码器的参数。解码器的任务是把这个“压缩版本”重新“扩展”成一张图像，也就是生成一个尽可能接近原始图像 $x$ 的重构图像 $x^{\prime }$。

理想情况下，重构出来的 $x^{\prime }$ 和原始图像 $x$ 应该非常相似。虽然它们不是完全一模一样，但我们希望它们在视觉和语义上尽可能接近。

为了衡量 $x$ 和 $x^{\prime }$ 之间有多接近，我们使用了均方误差(Mean Squared Error, MSE)这个指标来作为损失函数。它的数学表达式是：

$$L=\Vert x-x^{\prime }{\Vert }_2^2$$

这个公式的意思是：我们计算原始图像 $x$ 和重构图像 $x^{\prime }$ 每一个像素之间的差值，把所有差值平方后加起来，最终得到一个总的误差分数 $L$。误差越小，说明 $x^{\prime }$ 越接近 $x$，模型表现越好。

在训练过程中，我们会使用梯度下降等优化算法来最小化这个损失 $L$，一步一步调整编码器 $q_{\varphi }$ 和解码器 $p_{\theta }$ 的参数，使得重构结果 $x^{\prime }$ 越来越接近原始图像 $x$。

3 变分自编码器(VAEs)

变分自编码器(Variational Autoencoders, VAEs)在结构上与普通自编码器类似，但它们对潜在表示 $z$ 的分布进行了进一步约束。与其他生成模型一样，我们希望从一个潜在分布中采样潜在向量 $z$，再将其映射到图像空间。使用 VAE，我们可以指定这个潜在分布是一个均值为 $\mu$，标准差为 $\sigma$ 的高斯分布。

• 我们在训练生成模型时，希望从某种**“已知的分布”**中采样潜在变量 $z$，再通过解码器将其转化为图像。如果这个潜在分布非常复杂（比如没有规律或者每次都不一样），那我们就很难训练模型去“理解”它，更别说从中有效地采样了。
• 所以使用高斯分布的目的为：高斯分布数学性质很好，便于计算；且训练好模型之后，我们可以简单地从标准高斯分布 $N(0,\mathbf{I})$ 中采样，就能生成图像，不需要每次重新估计潜在分布。
  

为了训练一个 VAE，我们从输入图像 $x$ 开始，将其传入编码器。编码器会输出两个向量：一个是均值 $\mu$，一个是标准差 $\sigma$，它们一起定义了一个高斯分布。从这个高斯分布中，我们采样一个潜在表示 $z$。

在实际操作中，为了让采样过程可以被神经网络学习，我们使用了一个叫做“重参数化技巧”(reparameterization trick)的策略。

采样操作不是可导的，而神经网络训练依赖于反向传播(Backpropagation)，必须所有过程都能求导。

这意味着我们不直接从 $N(\mu ,\sigma )$ 中采样 $z$，而是先从标准正态分布中采样一个噪声项 $\epsilon \sim N(0,\mathbf{I})$，然后通过下面这个公式计算出 $z$：
$$z=\mu +\sigma \epsilon$$

这样做的目的是让整个采样过程可导，从而能够通过反向传播来训练整个网络。

我们现在从标准正态分布中采样 $\epsilon$，这是固定不变的。$\mu$ 和 $\sigma$ 只是普通神经网络的输出，可以正常反向传播求导。所以整个过程就变成了“确定性运算 + 一个已知的噪声”，网络仍然可以训练。

随后，采样得到的 $z$ 被传入解码器 $p_{\theta }(x|z)$，解码器将其上采样为一张图像，生成的图像记作 $x^{\prime }$，即重构图像。

训练 VAE 时，我们的目标是最大化输入图像 $x$ 的对数似然(log likelihood)。

在概率意义上，我们可以理解为：希望图像 $x$ 出现在模型的输出分布 $p_{\theta }(x)$ 中的概率越大越好。因此，我们就想最大化这个概率，也就是最大化 $p_{\theta }(x)$。但在高维正态分布中，概率本身通常非常小（比如 $0.00005$），在计算上容易出现数值不稳定的问题。所以我们取对数，变成最大化 $\log p_{\theta }(x)$。对数函数单调不减，不改变最大化的目标，而且让乘法变加法，更方便计算。

为此，我们最大化一个叫做“变分下界”(Variational Lower Bound, VLB)或“证据下界”(Evidence Lower Bound, ELBO)的目标函数：
$$\log p_{\theta }(x)\ge \log p_{\theta }(x)-D_{KL}(q_{\varphi }(z|x)\parallel p_{\theta }(z))$$

从概率角度说，就是希望模型分布 $p_{\theta }(x)$ 对真实数据 $x$ 的概率越大越好，也就是最大化 $\log p_{\theta }(x)$。但问题是：我们并不知道如何直接计算 $p_{\theta }(x)$，因为它需要对所有潜在变量 $z$ 做积分$p_{\theta }(x)=\int p_{\theta }(x|z)p(z)dz$。这个积分在高维空间中很难算，无法直接优化。

于是我们引入一个近似的分布 $q_{\varphi }(z|x)$（由编码器得到），代替真实但未知的 $p(z|x)$，并通过**变分推理（variational inference）**构造一个可以计算的下界。不等式右边的式子就叫做变分下界或证据下界。

其中，$D_{KL}$ 是 Kullback-Leibler（KL）散度，用来衡量两个概率分布之间的差异。由于两个不同分布之间的 KL 散度始终是正数，我们希望最小化 $q_{\varphi }(z|x)$ 和 $p_{\theta }(z)$ 之间的差异，从而最大化数据的对数似然 $\log p_{\theta }(x)$。

VAE 的损失函数如下：

$$L_{VLB}=\Vert x-x^{\prime }{\Vert }_2^2-D_{KL}\left(N(\mu ,{\sigma }^2)\parallel N(0,\mathbf{I})\right)$$

其中第一项是原图 $x$ 与重构图像 $x^{\prime }$ 之间的均方误差(MSE)，这部分可以看作是重建损失。第二项是我们学习到的高斯分布 $N(\mu ,{\sigma }^2)$ 与标准正态分布 $N(0,\mathbf{I})$ 之间的 KL 散度，它能让我们学习到的分布尽可能接近标准高斯分布。

变分下界 = 生成质量（重建越好越高） − 采样复杂度惩罚（分布越偏离越低）

我们优化 VAE 的目标，就是最大化这个下界，从而：既能重建出真实图像，又能保证潜在空间平滑、可控。

这就构成了变分自编码器的核心思想。

优点与缺点

自编码器和变分自编码器的一个优点是它们训练快速、实现简单。但是，它们也存在一个明显的缺点：生成的图像往往模糊，容易与真实图像区分开来。如下图所示，我们可以看到 VAE 生成的人脸是模糊的。这是因为 VAE 更倾向于生成“最可能”的图像，但却不善于表达某个非常具体或独特的细节。因此，最终生成的图像往往看起来像是多个真实图像的“平均脸”。

4 生成对抗模型(GANs)

生成对抗模型(Generative Adversarial Models, GANs)包含一个生成器网络和一个判别器网络。生成器根据从图像的潜在表示中采样得到的 $z$ 来生成“伪造”的图像。判别器接收一张图像作为输入，并判断这张图像是真实的还是伪造的。生成器和判别器在训练过程中以对抗的方式相互竞争。生成器试图欺骗判别器，而判别器的目标是成功地区分“伪造”图像与真实图像。

设 $p_r$ 表示真实图像的分布，$p_z$ 表示潜在空间的分布。训练中使用的损失函数为：

$$L=\underset{G}{\min }\underset{D}{\max }{\mathbb{E}}_{x\sim p_r(x)}[\log D(x)]+{\mathbb{E}}_{z\sim p_z(z)}[\log (1-D(G(z)))]$$

它表示的是一个“博弈最优值”（min-max）的过程：

• 第一项 ${\mathbb{E}}_{x\sim p_r(x)}[\log D(x)]$：判别器希望对真实图像 $x$ 的输出越接近 1（即“我认为是真的”），log 的值就越大。
• 第二项 ${\mathbb{E}}_{z\sim p_z(z)}[\log (1-D(G(z)))]$：判别器希望对生成图像 $G(z)$ 输出接近 0（“我认为是假的”），但生成器却想让这个值越大越好（即“我成功骗过了你”）。

所以我们让生成器 $\min$，让判别器 $\max$，两个网络在这个损失上互相拉扯、互相博弈。

优点与缺点

GANs 的优点是可以生成非常高质量的样本。其主要缺点是模式崩溃(mode collapse)：即生成的图像看起来都非常相似。这种现象是可以理解的，因为如果生成器发现只生成一种图像就可以成功欺骗判别器，那么它就不会尝试多样化输出，从而导致生成样本缺乏变化。

5 总结

本文简要介绍了三种常见的生成模型：自编码器、变分自编码器和生成对抗网络。自编码器通过压缩再重建数据来学习特征表示；VAEs 在此基础上引入概率建模，可以从高斯分布中采样生成新数据；GANs 则通过生成器与判别器的对抗训练，生成高质量图像。三者各有优劣，适用于不同场景，是理解和研究生成模型的重要基础。