旋转中心 TCP标定机械手抓料方式

Σίσυφος1900

已于 2024-08-03 17:32:15 修改

阅读量2.3k

点赞数 13

分类专栏： opencv Halcon 项目实践笔记文章标签：计算机视觉人工智能

于 2024-03-17 10:10:40 首次发布

本文链接：https://blog.csdn.net/weixin_39354845/article/details/136776474

版权

opencv 同时被 2 个专栏收录

35 篇文章

订阅专栏

Halcon 项目实践笔记

9 篇文章

订阅专栏

一、为什么要计算旋转中心？

机器视觉——旋转中心的标定_旋转标定-CSDN博客

在机械手抓料的时候传送带上过来的料可能是各个角度的，不同的位置，物料每次的角度不一样，机械手的末端工具中心与其自身的旋转中心不重合，这样如果我们没有做好机械手标定的话很难抓取，因此我们要做旋转中和和机械手TCP标定。

但是这里我要记录一下再项目中用的其他的一种方式，不需要标定，但是这个的精度可能就没有那么好了。但是做这个所有前提都是要做9点标定的。

那我命名第一方式就是项目抓取法。

机器视觉——旋转中心的标定_旋转标定-CSDN博客

TCP标定

一般机械手都会有建立新工具坐标系的功能，比如EPSON。TCP标定的本质就是求旧的工具坐标系与新的工具坐标系的旋转平移矩阵。一般是定义新的工具编号，放一个参考点，多次旋转U轴（旋转轴）（4次），然后移动X，Y（base下）使新工具坐标末端对准参考点，
对完之后点击示教就行了。以上使EPOSN的简单流程。

https://www.cnblogs.com/beta-1999/p/13121564.html

旋转中心标定

这两种方法的前提是都做好了九点标定

三点、五点拟合

计算偏移量（最重要的一步）

相似三角形

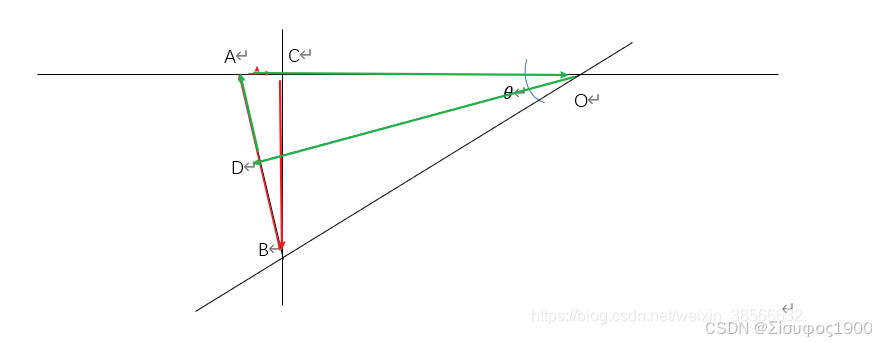
两点+角度计算旋转中心

计算方法1

角度a是我们通过机械手来转动的角度，因此三角形OP1P3 就是直角三角形，可以通过三角函数来计算出旋转半斤R，分别以P1 P2为圆心，R为半斤，计算两个圆的交点，有两个交点，判断是那个交点，最后得到O的位置即为旋转中心



        static List<double>  CalculateCircleCenter(double x1, double y1, double x2, double y2, double theta)
        {
            List<double> _centers = new List<double>(2);
            // 计算两点之间的距离
            double dx = x2 - x1;
            double dy = y2 - y1;
            double d = Math.Sqrt(dx * dx + dy * dy);

            // 计算圆的半径
            double thetaRad = theta * Math.PI / 180.0; // 角度转换为弧度
            double R = d / (2 * Math.Sin(thetaRad / 2));

            // 计算中点
            double Mx = (x1 + x2) / 2;
            double My = (y1 + y2) / 2;

            // 计算垂直于 AB 的单位向量
            double length = Math.Sqrt(dx * dx + dy * dy);
            double ux = -dy / length;
            double uy = dx / length;

            // 中点到圆心的距离
            double distance = Math.Sqrt(R * R - (d / 2) * (d / 2));

            // 圆心的两个可能坐标
            double x_center1 = Mx + distance * ux;
            _centers.Add(x_center1);
            double y_center1 = My + distance * uy;
            _centers.Add(y_center1);
            double x_center2 = Mx - distance * ux;
            _centers.Add(x_center2);
            double y_center2 = My - distance * uy;
            _centers.Add(y_center2);

            return _centers;
        }

计算方法2

P2是P1特征点绕O旋转角度A后的点

P3是P1和P2的延长线与以P1为圆心半径为r的交点

两点计算机械手旋转中心_两点一角度算旋转中心-CSDN博客

    double d;//P1和P2直接的距离
    double x0,y0;//旋转中心O
    double x1,y1,x2,y2;//p1和P2坐标
    double a;//旋转角度
    double xx,yy;//P3坐标
    double r ;//旋转半径
   
    x1 = this.Tools.CogIntersectLineCircleTool1.X1;
    y1 = this.Tools.CogIntersectLineCircleTool1.Y1;
    x2 = this.Tools.CogIntersectLineCircleTool2.X1;
    y2 = this.Tools.CogIntersectLineCircleTool2.Y1;
    
    d = Math.Sqrt((x2 - x1) * (x2 - x1)+(y2 - y1) * (y2 - y1));
    a =  this.Tools.CogAngleLineLineTool1.Angle;//a为弧度
    
    r = d / 2 / Math.Sin(a / 2);//
    

     // p3 的坐标是通过直线P1 P2 和圆（P1）半斤r 计算得出的
    //r / d = (xx - x1) / (x2 - x1);
    //r / d = (yy - y1) / (y2 - y1);
    xx = (1 - r / d) * x1 + (r / d) * x2;
    yy = (1 - r / d) * y1 + (r / d) * y2;
    
    double rr = 90 - (CogMisc.RadToDeg(a)/ 2);
    
    x0 = Math.Cos(Math.PI/2 - a / 2) * (xx - x1) - Math.Sin(Math.PI/2 - a / 2) * (yy - y1) + x1;
    y0 = Math.Cos(Math.PI/2 - a / 2) * (yy - y1) + Math.Sin(Math.PI/2 - a / 2) * (xx - x1) + y1;

二、项目抓取法

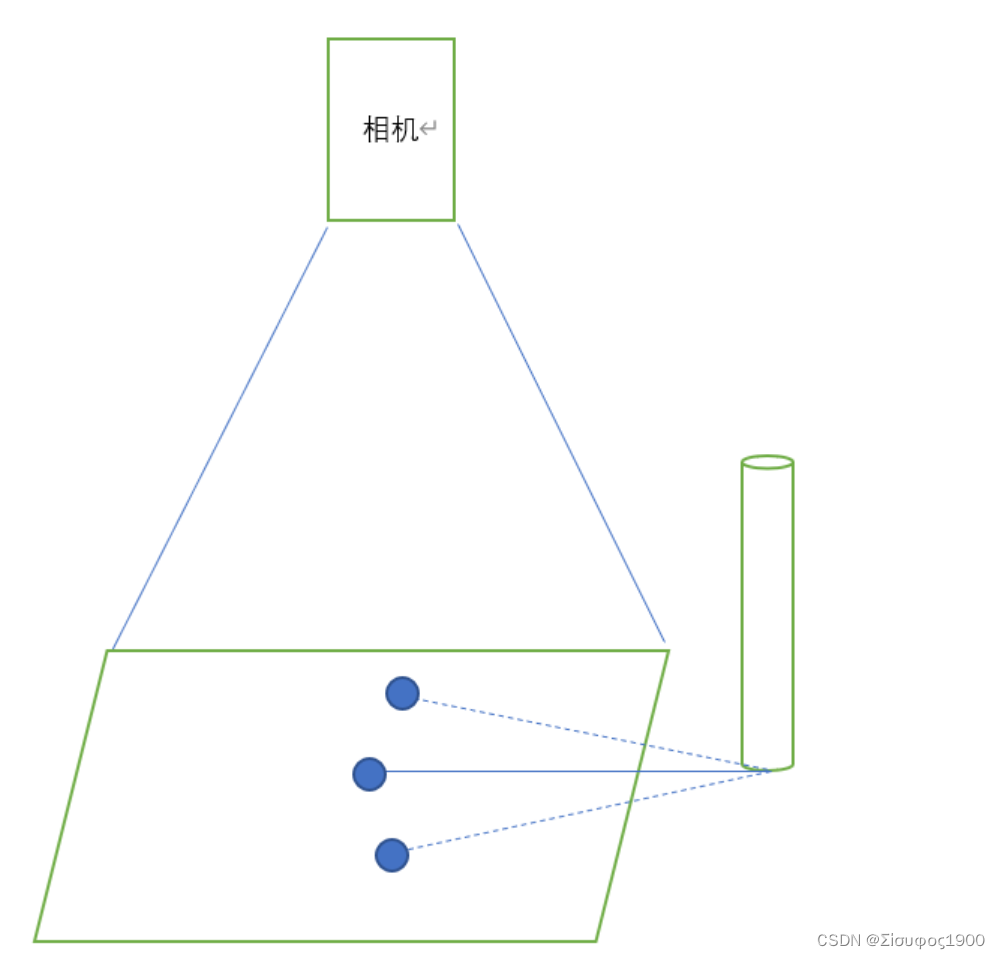
有一个前提就是相机不动，而且能排到传送带上的很大的视野，就是让每次产品的图片都在图像里面。示意图如下（盗图，懒得画）

计算偏移量

首先就是要做九点标定，做完之后我的思路是做一个位移补偿

我们可以先计算出相机的的位置，然后用机械手做运动，让其走到我们想要的那个产品中间，如果有微小的差距，那么我们可以通过计算移动机械手，计算出差值 delt_x 和 delt_y ，这个值应该是很小的，其实就是一个补偿，我们也可以多做几次然后做一个均值，还可以做个标记然后做运动，其原理是一样的。

计算角度

我们的产品上面是一个矩性的东西，所以很容易找到一条边如下

在图像上我们可以使用找边的方式，计算出来出两条边的中线，计算与X轴之间的夹角 angle_product,可以知道当前机械手的角度angle_tool ,angle_diff=angle_product-angle_tool ,然后我们可以先走平移，然后再旋转angle_diff ，这样就可以将产品拿到。

但是这种是对产品的精度要求没有那么高的，这种方法是可以的，如果更优点就是解决最短路径和最佳旋转角度的问题。