Nature 子刊丨用于材料原子建模的物理信息神经网络

作者：G.P.Purja Pun, R. Batra, R. Ramprasad  & Y. Mishin

单位：乔治梅森大学

01 摘要

材料的大规模原子计算机模拟在很大程度上依赖于原子间势预测原子上的能量和牛顿力。传统的原子间势是基于物理直觉的，但包含的可调参数很少，而且通常不准确。新兴的机器学习（ML）潜力在大型DFT数据库中实现了高精度的插值，但作为纯粹的数学结构，其向未知结构的可转移性较差。我们提出了一种新的方法，通过告知原子间键合的物理性质，可以显著提高ML势的可转移性。这是通过将一个相当通用的基于物理的模型（分析键序势）与神经网络回归相结合来实现的。这种方法被称为物理知情神经网络（PINN）势，通过开发Al的通用PINN势来证明。我们认为，开发基于物理的ML势是原子模拟领域中最有效的方法。

---

02 图表简介  

图：原子势发展的流程图。a传统的原子间势。b数学NN电位。c具有所有本地参数的物理通知NN（PINN）电位。d PINN电位，参数分为局部和全局。虚线矩形勾勒出需要参数优化的对象。PES是材料的势能面

图：PINN电位的准确性。a、 c用PINN势与DFT能量计算的a训练和c验证数据集中原子构型的能量。直线代表完美的配合。b、 d b训练和d验证数据集中的误差分布。

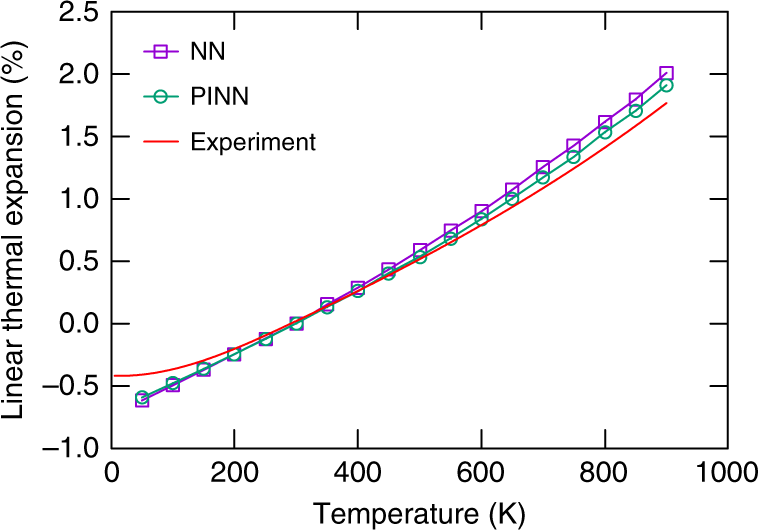
图：Al相对于室温的线性热膨胀（295 K） PINN和NN电位预测与实验的比较

图：NN和PINN电位的测试。a、 b从700开始的NVE MD模拟中Al中边缘位错的能量 K.c，d 1000、1500、2000和4000下NVT MD模拟中HCP-Al的能量 K.由PINN（a，c）和NN（b，d）势预测的能量与20，21的DFT计算进行了比较。直线代表完美贴合

图：铝晶体结构的能量-体积关系。由PINN势（线）和DFT计算（点）预测的能量的比较。六方紧密堆积（HCP）、体心立方（BCC）和简单立方（SC）结构。b A15（Cr3Si原型）、简单六边形（SH）和金刚石立方体（DC）结构

图：放大由PINN、NN、NN′、EAM和BOP势（曲线）和DFT计算（点）预测的能量-体积关系的排斥部分

图：原子力预测的测试。从700开始的NVE MD模拟中a，b验证数据库，c，d边缘位错的原子力的x分量 K、 以及e，f在300、600、1000、1500、2000和4000的NVT MD模拟中的HCP Al K.由PINN（a，c，e）和NN（b，d，f）势预测的力与参考文献中的DFT计算进行了比较。

图：DFT与电势的比较。用于训练和验证的DFT数据库中原子配置的能量和EAM Al势54和BOP势的预测进行了比较。BOP参数已拟合到DFT数据库中并永久固定。包括PINN潜在预测以供比较。直线代表完美贴合

03 参考文献

Pun G P P, Batra R, Ramprasad R, et al. Physically informed artificial neural networks for atomistic modeling of materials[J]. Nature communications, 2019, 10(1): 2339..

关注公众号：工大博士科研日常分享

小编有话说：本文仅作科研人员学术交流，由于小编才疏学浅，不科学之处欢迎批评。如有其他问题请随时联系小编。欢迎关注，点赞，转发，欢迎互设白名单。投稿、荐稿：MechanicsAI@163.com