论文标题:A Collaborative Sensor Fusion Algorithm for Multi-Object Tracking Using a Gaussian Mixture Probability Hypothesis Density Filter
发表期刊/会议:2015 IEEE 18th International Conference on Intelligent Transportation Systems
问题:后期融合策略通过分享经过处理/过滤的估计结果(如目标边界框/轨迹),可以避免数据量和通信信道的限制,但仍然存在时间和空间对齐问题:
1.时间对齐:由于无线通信链路的可变延迟,通过通信传输收到的变量可能不能代表物体在收到时的真实状态。如果传递的是原始测量数据而不是轨迹,这通信延迟问题更严重。
2.空间对齐:发送车辆和接收车辆的局部坐标系存在差异;另外,发送车辆和接收车辆位置的不确定性使空间对齐更具挑战。
1 协同GM-PHD滤波器
为了解决协同多目标跟踪的问题,提出了一个协同GM-PHD(Gaussian Mixture Probability Hypothesis Density)滤波器(C-GM-PHD),主要利用一个融合模块来扩展GM-PHD滤波器,能够将来自其他车辆的GM-PHD滤波器的PHD强度与自车的PHD强度相融合,以此扩展Ego车FOV进而提高估计的可信度。
C-GM-PHD滤波器的流程方框图:

假设在第
k
−
1
k-1
k−1个时间步的后验强度是一个由
J
k
−
1
J_{k-1}
Jk−1个权重为
w
k
−
1
w_{k-1}
wk−1,均值为
m
k
−
1
m_{k-1}
mk−1,协方差为
P
k
−
1
P_{k-1}
Pk−1的分量组成的高斯混合物:

那么,C-GM-PHD滤波器计算后验强度
v
k
v_{k}
vk(x)的步骤如下:
1) 预测
在第k个时间步的预测强度也是一个高斯混合物:
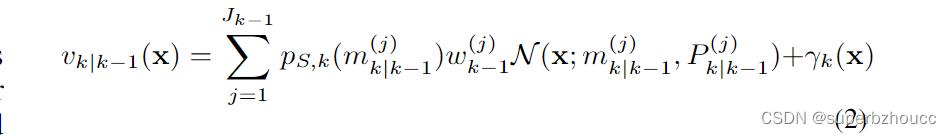
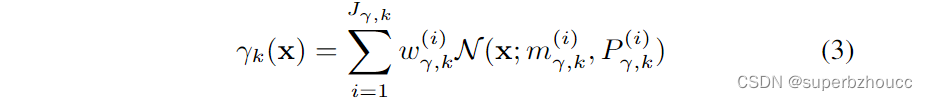
其中,
γ
k
γ_{k}
γk(x)是具有
J
γ
,
k
J_{γ,k}
Jγ,k个分量的 birth 强度;而
p
S
,
k
(
m
k
∣
k
−
1
(
j
)
)
p_{S,k}(m^{(j)}_{k|k-1})
pS,k(mk∣k−1(j))是第
j
j
j个高斯分量在第
k
k
k个时间步的生存概率。(为了简单起见,所提出的滤波器实现中不包括生成目标。)
然后,使用无迹卡尔曼滤波(UKF)来计算估计的GM分量的预测平均值和协方差:

其中
χ
k
∣
k
−
1
(
i
)
χ^{(i)}_{k|k-1}
χk∣k−1(i)是通过unscented transform (UT)计算得到的sigma点,
Υ
(
i
)
Υ^{(i)}
Υ(i)是相对应的权值。
Λ
Λ
Λ表示状态的维度,UKF使用的sigma点的总数为2Λ+1。
2) 更新
对于一组测量值
Z
k
Z_k
Zk,更新步骤产生了一个后验强度:

其中,
更新步骤中使用的参数是干扰水平
κ
k
κ_{k}
κk(z),检测概率
p
D
,
k
(
m
k
∣
k
−
1
(
i
)
)
p_{D,k}(m^{(i)}_{k|k-1})
pD,k(mk∣k−1(i))取决于第
i
i
i个高斯分量的平均值、观测模型
H
k
H_k
Hk和观测噪声协方差
R
k
R_k
Rk。
3) 裁剪和合并
在更新步骤之后,高斯分量的数量会随着测量次数的增加而呈二次方增长。为了限制高斯的数量,通过截断具有弱权重的高斯分量,即保留权重高于某个阈值的高斯分量,得到高斯混合的近似后验强度。然后,从保留的高斯分量中找到所有平均值在马氏距离U内的高斯分量
L
=
{L=}
L={
i
∈
I
∣
(
m
k
(
i
)
−
m
k
(
j
)
)
T
(
P
k
(
i
)
)
−
1
(
m
k
(
i
)
−
m
k
(
j
)
)
≤
U
i ∈I|(m^{(i)}_{k}−m^{(j)}_k )^{T}(P^{(i)}_{k})^{−1}(m^{(i)}_{k} −m^{(j)}_{k} ) ≤U
i∈I∣(mk(i)−mk(j))T(Pk(i))−1(mk(i)−mk(j))≤U},将它们合并在一起:

形成一个具有最高权重的高斯分量,用它来近似所有相互接近的高斯分量。
4) 融合
ego车辆在通过无线通信接收到其他协作车辆发送的信息(GM-PHD强度)后,再与自车的GM-PHD强度融合。
空间对齐(坐标转换):
将强度从发送车辆的坐标系转换到以自车坐标系中。由于两辆车的位置姿态不确定,两个坐标系之间的转换并不是已知的。因此,采用近似变换
近似变换:
x
C
W
\mathbf{x}^{W}_{\mathcal{C}}
xCW表示从全局坐标系
W
W
W 到协作车辆坐标系
C
\mathcal{C}
C 的变换。协作车在自己的坐标系下跟踪一个目标
N
C
\mathcal{N}\mathcal{C}
NC;变换
x
N
C
C
\mathbf{x}^{\mathcal{C}}_{\mathcal{N}\mathcal{C}}
xNCC表示目标的位置。跟踪到的目标的位置可以用变换
x
N
C
W
=
x
C
W
+
x
N
C
C
\mathbf{x}^{W}_{\mathcal{N}\mathcal{C}}= \mathbf{x}^{W}_{\mathcal{C}} +\mathbf{x}^{\mathcal{C}}_{\mathcal{N}\mathcal{C}}
xNCW=xCW+xNCC在全局坐标系中表示。变换
x
N
C
E
\mathbf{x}^{\mathcal{E}}_{\mathcal{N}\mathcal{C}}
xNCE可以得到
x
W
E
+
x
N
C
W
\mathbf{x}^{\mathcal{E}}_{W}+\mathbf{x}^{W}_{\mathcal{N}\mathcal{C}}
xWE+xNCW,其中
x
W
E
=
−
x
E
W
\mathbf{x}^{\mathcal{E}}_{W}=-\mathbf{x}^{W}_{\mathcal{E}}
xWE=−xEW。

首先,通过进行从W到协作车辆坐标系
C
(
x
C
W
)
\mathcal{C}(\mathbf{x}^{W}_{\mathcal{C}})
C(xCW)和从
C
\mathcal{C}
C到目标坐标系
(
x
N
C
C
)
(\mathbf{x}^{\mathcal{C}}_{\mathcal{N}\mathcal{C}})
(xNCC)的变换,获得了非协作车辆
N
C
\mathcal{N}\mathcal{C}
NC(目标)在全局坐标系W下的坐标
x
N
C
W
\mathbf{x}^{W}_{\mathcal{N}\mathcal{C}}
xNCW:

通过关于变量均值的一阶泰勒级数展开来近似
x
N
C
W
\mathbf{x}^{W}_{\mathcal{N}\mathcal{C}}
xNCW,通过将
x
N
C
W
\mathbf{x}^{W}_{\mathcal{N}\mathcal{C}}
xNCW应用于变量均值得到近似变换的均值,即
x
^
N
C
W
=
f
(
x
^
C
W
,
x
^
N
C
C
)
\hat{\mathbf{x}}^{W}_{\mathcal{N}\mathcal{C}}=f(\hat{\mathbf{x}}^{W}_{\mathcal{C}}, \hat{\mathbf{x}}^{\mathcal{C}}_{\mathcal{N}\mathcal{C}})
x^NCW=f(x^CW,x^NCC),该变换的协方差矩阵为:

其中,P1和P2分别为变换
x
C
W
\mathbf{x}^{W}_{\mathcal{C}}
xCW和
x
N
C
C
\mathbf{x}^{\mathcal{C}}_{\mathcal{N}\mathcal{C}}
xNCC的协方差,J为变换的雅克比系数:

变换
x
W
E
\mathbf{x}^{\mathcal{E}}_{W}
xWE是通过从W到
E
\mathcal{E}
E的反向变换
(
x
E
W
)
(\mathbf{x}^{W}_{\mathcal{E}})
(xEW)得到的,反向变换的协方差矩阵(如P′)是由给定的变换
x
E
W
\mathbf{x}^{W}_{\mathcal{E}}
xEW的协方差矩阵(如矩阵P)估计的,即:

其中,R是反向变换方程的雅克比系数。最后,使用变换
x
W
E
\mathbf{x}^{\mathcal{E}}_{W}
xWE和
x
N
C
W
\mathbf{x}^{W}_{\mathcal{NC}}
xNCW得到从
E
\mathcal{E}
E到目标的变换
(
x
N
C
E
)
(\mathbf{x}^{\mathcal{E}}_{\mathcal{NC}})
(xNCE)及其协方差矩阵,与从变换
x
C
W
\mathbf{x}^{W}_{\mathcal{C}}
xCW和
x
N
C
C
\mathbf{x}^{\mathcal{C}}_{\mathcal{NC}}
xNCC得到变换
x
N
C
W
\mathbf{x}^{W}_{\mathcal{NC}}
xNCW的情况类似。
一旦所有高斯的均值和协方差在ego车辆的坐标系中表示出来,它们就可以与自车本地C-GM-PHD强度融合。
鉴于后验强度是高斯混合模型,为了保留位置PDF的GM形式,使用指数高斯混合模型的近似。
GCI(Generalized Covariance Intersection)融合简化为依次对v1和v2的每一对高斯分量应用CI融合,从而得到融合强度中Jk(v1)×Jk(v2)分量的总数。
上述方法是为FOV完全重叠的传感器的融合而开发的,在一般情况下,当定义GM的领域不一样时(即不同传感器的FOV不完全重叠时),它的效果并不好。GCI只对位于多个传感器的共同FOV中的组件分配重要的权重。
融合算法:

只对相互接近的高斯分量应用CI(第5-17行),而对其余的高斯分量保持不变(第19-23行)。高斯分量的紧密性通过马氏距离和阈值UF来表示(第7行)。融合后的集合的cardinality被计算为两个初始集合的加权cardinality(第18行)。在融合之后,将相互接近的部分合并。这种方法使得能够在两个传感器的共同FOV中获得与使用GCI时相同的融合经验,同时又能跟踪仅在一个传感器FOV中的所有目标。
5) 提取
从RFS强度的GM表示中直接提取多目标状态的估计。权重大于某个阈值Te(例如,Te>0.5)的高斯分类被提取出来,代表最可能的估计值。
2 协同车辆跟踪
2.1 运动学状态和运动模型
使用一个矩形代表跟踪目标,其状态空间是运动学和形状参数变量的组合:

其中x和y是矩形中心的欧几里得坐标,ν是速度,θ表示航向角,ω是转弯率。矩形的长度和宽度分别用L和W来表示。对于状态传播,选择了恒定转弯率和速度(CTRV)运动模型,用物体的尺寸对其进行了增广,假定为常数。
2.2 测量模型
在每个时间步,激光雷达返回一组测量点(点云)。每个点在二维的极坐标中被定义(使用范围r和方位β),不确定性通过协方差矩阵R = [σr 0 0 σβ]表示。假设距离和方位的测量是相互独立的。使用目标检测算法(算法二)对点云进行预处理,以获得z = [x,y,θ]>形式的测量值,其中一个测量值对应于被认为是一个物体(x和y代表物体矩形的中心,而θ代表其方向)。PHD强度使用UKF和物体测量值z进行更新。
目标检测:

(i) 将测量点从极坐标转换为笛卡尔坐标,
(ii) 使用DBSCAN算法进行聚类,同时忽略少于两点的聚类,
(iii) 对每个聚类进行线和角拟合,
(iv) 矩形拟合和特征点提取。
一个经过处理的测量包含一个矩形的中心和方向。
矩形中心的测量直接用于更新(21)中的状态向量
x
\mathbf{x}
x的
x
x
x和
y
y
y变量。矩形方向有π rad的模糊性(从静态激光雷达扫描中不能确定物体的方向,只能确定其方向)。因此,在更新状态向量的航向θx之前,需要调整方向测量θz,使方向测量和状态航向之间的差异被包裹在区间[-π/2, π/2] 内:

2.3 遮挡和FOV模型
遮挡和FOV模型的目的是为了能够跟踪暂时被遮挡或位于传感FOV边界的物体。这是通过将不可能被传感器探测到的目标的探测概率pD,k(m(i) k|k-1)设置为一个低值来实现的。如果不这样做,C-GM-PHD滤波器会迅速降低这些目标的权重并将其丢弃。
调整了Granstrom等人提出的occlusion 模型,对两个矩形角(最小和最大的轴承角)的occlusions 进行验证,并通过FOV验证来增广它。对所有其他估计在传感器和感兴趣的物体之间的物体,对遮挡进行验证。检测概率的降低与估计的权重成正比。一个被遮挡的角落会使pD最大减少0.5。高斯kernels被用来平滑从可见区到遮挡区的过渡。为了跟踪传感器视野之外的目标(通过协作),将高斯kernels沿传感器视野的边界放置。对于处于边界或FOV之外的目标,会降低pD。

3 实验
实验是在一个亚微观的高保真机器人模拟器中进行。使用模拟的雪铁龙C-ZERO汽车,它是用真实的C-ZERO的CAD模型创建的,并使用真实的汽车进行校准。每辆用于传感的汽车都配备了一个正面的Ibeo LUX激光雷达,一个GNSS设备,一个罗盘和一个无线通信设备。分辨率、精度、范围和其他传感器的特性都是使用传感器的数据表进行校准的。数据集包含了在20次独特的模拟运行中收集的数据。在每次运行中,车辆按照预先确定的轨迹运行一个开环控制器。执行器和传感器(如激光雷达)的噪声有助于生成传感数据的随机性。
4 总结
提出了一种对多辆汽车进行协作跟踪的方法,该方法将高斯混合概率假设密度滤波器(GM-PHD)与协作融合算法进行扩展。以先检测后跟踪的方式进行预处理,并使用矩形形状模型对汽车进行跟踪。为了扩大单个车辆的视场,提高多辆车可观察到的目标区域的估计置信度,在车辆之间交换PHD强度,并使用一个基于广义协方差交叉融合的算法在协同GM-PHD滤波器中进行融合。
- 提出了一种基于GM-PHD滤波器和考虑到车辆形状的车辆检测模型的车辆跟踪方法。当使用PHD滤波器进行目标跟踪时,轨迹传输被简化为PHD强度传输。
- 提出了一种GM-PHD密度协同融合方法,其中车辆的视场不需要重叠,可以通过使用通信将单个车辆的FOV扩展到其传感器的极限之外,并在一个目标被多个车辆观察的情况下降低估计的不确定性。











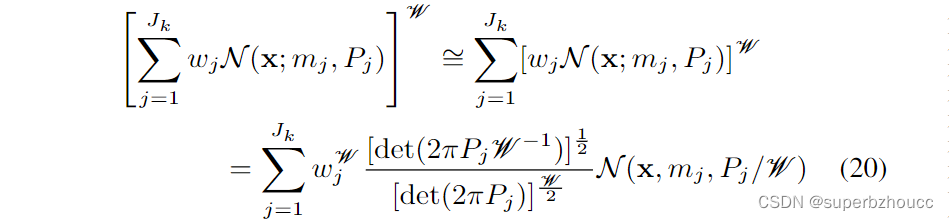
















 965
965

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








