传统点云分割三部曲（三）——CPC（Constrained Planar Cuts）

一、前言

传统方法进行点云分割也有很好的效果，这篇博客是本系列的第三篇，介绍的是发表于2015年CVPR上的CPC算法，CPC原文 。CPC在LCCP的基础上继续深入，LCCP判断邻接超体素之间的凹凸性，将凹边视作无效边，最后沿着凸边对超体素做聚类，再滤除超体素个数少的类，即可实现对物体的分割，效果如下：

第一幅图中的一个个白色正方形可以视作超体素，凸边凹边奇异边也用不同颜色标识了出来，可以看到这个阶梯状的物体在使用LCCP过后，从白色的桌面上被分离出来了。在某些场景下，这种程度的分割已经足够。但试想这样一个场景，在码垛的时候，一堆货物堆放成了如图所示的阶梯状，为了能顺利拆垛，就还需要对这一整个物体做进一步的分割。

可以看到同一物体中的不同部分之间是存在一些凹边的，所以CPC的方法在LCCP的基础上，利用了局部凹性对物体的不同部分做进一步的分割，在一些数据集上取得了很好的效果。

二、方法部分

2.1 Local concavity evidence extraction

首先使用VCCS对点云做预分割，分割的结果是获得一些“补丁”形状的超体素$\overrightarrow{p_i}=(\overrightarrow{x_i},\overrightarrow{n_i},N_i)$ ，$\overrightarrow{x_i}$是超体素的质心，$\overrightarrow{n_i}$是法向，$N_i$是一个集合，包含了当前超体素的邻接边信息。有了邻接图信息之后，使用LCCP来对其中的每条边进行凹凸性判断，判断基于一个非常直观的几何规律。定义超体素质心连线$\vec{d}=\frac{\overrightarrow{x_1}-\overrightarrow{x_2}}{\Vert \overrightarrow{x_1}-\overrightarrow{x_2}{\Vert }_2}$，${\alpha }_1$和${\alpha }_2$分别是两条法线与质心连线的夹角，定义$\alpha ={\alpha }_1-{\alpha }_2$，可以观察到对于凸连接$\alpha <0$，即$(\overrightarrow{n_1}-\overrightarrow{n_2})\cdot d>0$，凹连接$\alpha >0$。

为了解决一些具体的问题，作者对上述内容进行扩展，提出了两条凸性判断准则——Extended Convexity Criterion（EC）和Sanity criterion（SC），具体内容请回看上一篇博客。

2.2 Semi-global partitioning

2.2.1 Euclidean edge cloud

首先将邻接图转化成Euclidean edge cloud（EEC），在连接两个超体素边的中点位置添加一个点，同时这个点需要保留 $\vec{d}$ 和 $\alpha$ 信息。

2.2.2 Geometrically constrained partitioning

本文的分割方法的核心其实是RANSAC，通过其来找到得分最大的分割模型（本文只考虑平面模型）。经典RANSAC的评分标准是统计距离拟合模型符合阈值的点的个数，迭代结束后具有最多点的模型被视作最终结果。CPC评分标准如下：
$$S_m=\frac{1}{|{\mathcal{P}}_m|}\sum _{i\in {\mathcal{P}}_m}{\omega }_i$$
其中${\mathcal{P}}_m$是到平面距离小于预设阈值的EEC点集，${\omega }_i$是每个EEC点的权重，定义如下，$\mathcal{H}$是阶跃函数
$$\omega (\alpha )=\mathcal{H}(\alpha -{\beta }_{\text{thresh}})$$
经过这个函数，所有凸边的权重都被设置为0。有了这样的评分函数，分割会倾向于在support region中包含更多的凹点，同时又要尽可能少的包含凸点，因为凸点只增加$|{\mathcal{P}}_m|$也会使得评分变低。所以${\mathcal{S}}_m$数值应位于0到1之间，为0时说明整个support region中只包含凸点，为1则全为凹点。

3. 文中指出了一种特殊情况，就是分割平面可能只简单地追求更多地凹点，而导致错误地分割，如下图B所示：
   
   令${\vec{s}}_m$代表分割平面的法向量，$\overrightarrow{d_i}$是第 $i$ 个点包含的 $\vec{d}$ 信息（前文提到过的质心连线），为了找到垂直于${\vec{d}}_i$的分割平面，作者提出了Directional Weighted RANSAC:
   $$\begin{gathered} S_m=\frac{1}{|{\mathcal{P}}_m|}\sum _{i\in {\mathcal{P}}_m}{\omega }_i{t}_i \\ {t}_i=\{\begin{array}{ll}|{\vec{d}}_i\cdot {\vec{s}}_m|& iisconcave\\ 1& iisconvex\end{array} \end{gathered}$$
   使用这个评分函数后，B中的分割模型会获得接近0的分数，而C中的分割模型分数会很高。

2.2.3 Locally constrained cutting

如果不做特殊处理，一个平面切下去只能把物体分成两部分。有些情况，这种二分切割会出现问题，如下图B所示。所以需要找到一种只切割局部的方法，希望获得下图C中的结果。

作者提出，对于每次分割，都会进行一次欧式聚类。原文中说的“euclidean clustering of all edge-points using a cluster threshold equal to the seed-size of the supervoxels.”，这个seed-size怎么得到呢？我不太清楚。然后对每个聚类单独计算评分，由于太耗时，实际只会对${\mathcal{S}}_m$最高的模型做上述操作。

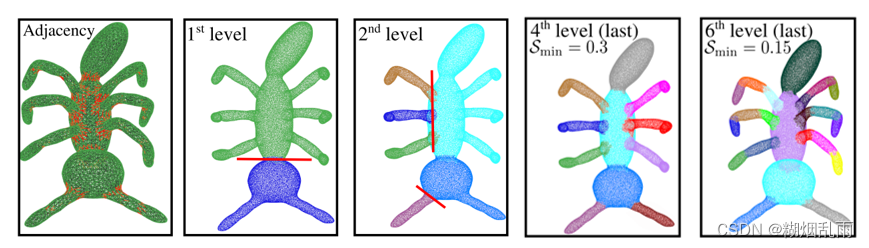
整个分割流程会在新获得的segment上不断重复，直到分数无法超过预设分数阈值${\mathcal{S}}_{min}$或者所含超体素个数小于$N_{min}$。

三、实际效果与调参建议