H无穷控制学习笔记——H无穷控制

最新推荐文章于 2024-02-23 12:00:01 发布

置顶一饮丶一啄

最新推荐文章于 2024-02-23 12:00:01 发布

阅读量8.2w

点赞数 47

分类专栏： MATLAB 现代控制文章标签：算法 matlab

本文链接：https://blog.csdn.net/weixin_45454343/article/details/114443288

版权

MATLAB 同时被 2 个专栏收录

11 篇文章 29 订阅

订阅专栏

现代控制

5 篇文章 4 订阅

订阅专栏

一、 $H_\infty$ 控制总纲

针对广义系统：
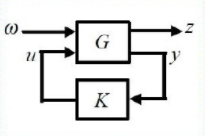
在这里插入图片描述
其中，G(s)是一个线性定常系统，其状态空间描述为： $\dot x=Ax+B_1w+B_2u\\z=C_1x+D_{11}w+D_{12}u\\y=C_2x+D_{21}w+D_{22}u$ 其中， $x\in R^n$ 是状态向量， $u\in R^m$ 是控制输入， $y\in R^p$ 是测量输出， $z\in R^r$ 是被调输出， $w\in R^q$ 是外部扰动，K(s)是控制器的传递函数。

目的是设计一个控制器 $u (s) = K (s) y (s)$ ，使得闭环系统满足：

闭环系统内部稳定，即闭环系统状态矩阵的所有特征值均在左半开复平面上；
从扰动输入w到被调输出z的闭环传递函数 $T_{wz}(s)$ 的 $H_\infty$ 范数小于1，即 $||T_{wz}(s)||_{\infty}<1$ 。

二、状态反馈 $H_\infty$ 控制

1、闭环传递函数的确定

假定系统的状态是可测的，要求设计一个静态状态反馈控制器 $u = K x$ 使得原线性定常系统渐进稳定且闭环传递函数 $||T_{wz}(s)||_{\infty}<1$ 。

原系统为： $\dot x=Ax+B_1w+B_2u\\z=C_1x+D_{11}w+D_{12}u$

将 $u = K x$ 代入该系统得到： $\dot x=(A+B_2K)x+B_1w\\z=(C_1+D_{12}K)x+D_{11}w$

状态空间方程到传递函数的转换关系为 $G(s)=C(sI-A)^{-1}B+D$ ，套用得到闭环传递函数 $T_{wz}(s)$ ： $T_{wz}(s)=(C_1+D_{12}K)[sI-(A+B_2K)]^{-1}B_1+D_{11}$

2、状态反馈 $H_\infty$ 控制器

而根据定理：在这里插入图片描述
当且仅当存在一个对称正定矩阵P，使得：
$\begin{bmatrix} (A+B_2K)^TP+P(A+B_2K) & PB_1 & (C_1+D_{12}K)^T \\ B_1^TP & -I & D_{11}^T \\ C_1+D_{12}K & D_{11} & -I \end{bmatrix}<0$

为了求解未知矩阵变量K和P，使用变量替换法，将其转化为一个等价的关于新变量的线性矩阵不等式。
对其分别左乘和右乘矩阵 $diag\{P^{-1},I,I\}$ ，得到：
$\begin{bmatrix} (AP^{-1}+B_2KP^{-1})+(AP^{-1}+B_2KP^{-1})^T & B_1 & (C_1P^{-1}+D_{12}KP^{-1})^T \\ B_1^T & -I & D_{11}^T \\ C_1P^{-1}+D_{12}KP^{-1} & D_{11} & -I \end{bmatrix}<0$

定义 $X=P^{-1}$ 和 $W = K X$ ，得到：
$\begin{bmatrix} (AX+B_2W)+(AX+B_2W)^T & B_1 & (C_1X+D_{12}W)^T \\ B_1^T & -I & D_{11}^T \\ C_1X+D_{12}W & D_{11} & -I \end{bmatrix}<0$
定理：对于原线性定常系统，存在一个状态反馈 $H_\infty$ 控制器，当且仅当存在一个对称正定矩阵X和矩阵W(W不对称正定)，使得 $\begin{bmatrix} (AX+B_2W)+(AX+B_2W)^T & B_1 & (C_1X+D_{12}W)^T \\ B_1^T & -I & D_{11}^T \\ C_1X+D_{12}W & D_{11} & -I \end{bmatrix}<0$ 和 $X > 0$ 成立，并且可行解 $X^*$ 和 $W^*$ 组成的 $u=W^*(X^*)^{-1}x$ 是系统的一个状态反馈 $H_\infty$ 控制器。

该矩阵不等式是矩阵变量X和W的一个线性矩阵不等式，可利用LMI工具箱的求解器feasp来求解。

3、状态反馈 $\gamma$ -次优 $H_\infty$ 控制器

对于给定标量 $\gamma>0$ ，为了求系统的状态反馈 $\gamma$ -次优 $H_\infty$ 控制器，由于：
$||T_{wz}(s)||_{\infty}<\gamma$ 得到： $||\gamma^{-1}T_{wz}(s)||_{\infty}<1$ 得到：
$||\gamma^{-1}T_{wz}(s)||_{\infty}=||\gamma^{-1}(C_1+D_{12}K)[sI-(A+B_2K)]^{-1}B_1+\gamma^{-1}D_{11}||<1$

因此，可以通过用 $\gamma^{-1}C_1$ 、 $\gamma^{-1}D_{12}$ 和 $\gamma^{-1}D_{11}$ 代替原矩阵 $C_1$ 、 $D_{12}$ 和 $D_{11}$ ，按原设计思路即可得到状态反馈 $\gamma$ -次优 $H_\infty$ 控制器。

此时，原矩阵不等式可写为：
$\begin{bmatrix} (AX+B_2W)+(AX+B_2W)^T & B_1 & \gamma^{-1}(C_1X+D_{12}W)^T \\ B_1^T & -I & \gamma^{-1}D_{11}^T \\ \gamma^{-1}(C_1X+D_{12}W) & \gamma^{-1}D_{11} & -I \end{bmatrix}<0$

将上式分别左乘和右乘矩阵 $diag\{I,I,\gamma I\}$ ，得到： $\begin{bmatrix} (AX+B_2W)+(AX+B_2W)^T & B_1 & (C_1X+D_{12}W)^T \\ B_1^T & -I & D_{11}^T \\ C_1X+D_{12}W & D_{11} & -\gamma^2I \end{bmatrix}<0$
因此，对于原线性定常系统，存在一个状态反馈 $\gamma$ -次优 $H_\infty$ 控制器，当且仅当存在一个对称正定矩阵X和矩阵W(W不对称正定)，使得 $\begin{bmatrix} (AX+B_2W)+(AX+B_2W)^T & B_1 & (C_1X+D_{12}W)^T \\ B_1^T & -I & D_{11}^T \\ C_1X+D_{12}W & D_{11} & -\gamma^2I \end{bmatrix}<0$ 和 $X > 0$ 成立，并且可行解 $X^*$ 和 $W^*$ 组成的 $u=W^*(X^*)^{-1}x$ 是系统的一个状态反馈 $\gamma$ -次优 $H_\infty$ 控制器。

4、状态反馈最优 $H_\infty$ 控制器

基于状态反馈 $\gamma$ -次优 $H_\infty$ 控制器的存在条件，建立这样一个优化问题：
$min~\rho\\s.t.~\begin{bmatrix} (AX+B_2W)+(AX+B_2W)^T & B_1 & (C_1X+D_{12}W)^T \\ B_1^T & -I & D_{11}^T \\ C_1X+D_{12}W & D_{11} & -\rho I \end{bmatrix}<0\\X>0$

该问题是一个具有线性矩阵不等式约束和线性目标函数的凸优化问题，可以应用LMI工具箱的求解mincx来求解。如果该问题有解，就可以得到系统的状态反馈最优 $H_\infty$ 控制器。

三、输出反馈 $H_\infty$ 控制

1、设计思路

当系统状态难以测量时，可以选择输出反馈的控制方式。
要求设计一个输出反馈控制器 $u = K y$ 使得原线性定常系统渐进稳定且闭环传递函数 $||T_{wz}(s)||_{\infty}<1$ 。

首先，需要假定： $A,B_2,C_2)$ 是能稳能检测的； $D_{22}=0$ 。

将 $u = K y$ 写成状态空间形式为：
$\dot{\widehat x}=A_K\widehat x+B_Ky\\u=C_K\widehat x+D_Ky$

其中， $\widehat x$ 是控制器的状态，而 $A_K$ 、 $B_K$ 、 $C_K$ 、 $D_K$ 是待确定的控制器参数矩阵。

将控制器代入到原系统得到新的闭环系统为：
$\begin{bmatrix}\dot x \\ \dot{\widehat x} \end{bmatrix}= \begin{bmatrix}A+B_2D_KC_2 & B_2C_K \\ B_KC_2 & A_K \end{bmatrix} \begin{bmatrix}x \\ \widehat x \end{bmatrix}+ \begin{bmatrix}B_1+B_2D_KD_{21} \\ B_KD_{21} \end{bmatrix}w\\ z=\begin{bmatrix}C_1+D_{12}D_KC_2 & D_{12}C_K \end{bmatrix} \begin{bmatrix}x \\ \widehat x \end{bmatrix}+(D_{11}+D_{12}D_KD_{21})w$

简化为：
$\dot \xi=A_{c1}\xi+B_{c1}w\\ z=C_{c1}\xi+D_{c1}w$

因此，根据定理：在这里插入图片描述
新的闭环系统渐近稳定且 $H_\infty$ 范数小于1的充要条件是存在一个对称正定矩阵 $X_{c1}$ ，使得：
$\begin{bmatrix} A_{c1}^TX_{c1}+X_{c1}A_{c1} & X_{c1}B_{c1} & C_{c1}^T \\ B_{c1}^TX_{c1} & -I & D_{c1}^T \\ C_{c1} & D_{c1} & -I \end{bmatrix}<0$

2、消元法设计输出反馈 $H_\infty$ 控制器

定理：原线性定常系统存在一个输出反馈 $H_\infty$ 控制器，当且仅当存在对称正定矩阵X和Y(Y也对称正定)，使得：

$\begin{bmatrix} N_0 & 0 \\ 0 & I \end{bmatrix}^T\begin{bmatrix} A^TX+XA & XB_1 & C_1^T \\ B_1^TX & -I & D_{11}^T \\ C_1 & D_{11} & -I \end{bmatrix}\begin{bmatrix} N_0 & 0 \\ 0 & I \end{bmatrix}<0$
$\begin{bmatrix} N_c & 0 \\ 0 & I \end{bmatrix}^T\begin{bmatrix} AY+YA^T & YC_1^T & B_1 \\ C_1Y & -I & D_{11} \\ B_1^TC_1 & D_{11}^T & -I \end{bmatrix}\begin{bmatrix} N_c & 0 \\ 0 & I \end{bmatrix}<0$
$\begin{bmatrix} X & I \\ I & Y \end{bmatrix}\ge0$

其中， $N_0$ 和 $N_c$ 分别是以子空间 $ker([C_2~~D_{21}])$ 和 $ker([B_2^T~~D_{12}^T])$ 中任意一组基向量作为列向量所构成的矩阵。可以应用LMI工具箱的求解器feasp来求解。

按以下步骤设计所需要的输出反馈 $H_\infty$ 控制器：

求解满足以上定理的矩阵X和Y；
求解满足 $X-Y^{-1}=X_2X_2^T$ 的矩阵 $X_2\in R^{n\times n_K}$ ，其中 $n_K$ 可以选成矩阵 $X-Y^{-1}$ 的秩;
用 $X$ 和 $X_2$ 构造 $X_{c1}=\begin{bmatrix} X & X_2^T \\ X_2 & I \end{bmatrix}$ ;
将矩阵 $X_{c1}$ 代入到矩阵不等式 $H_{X_{c1}}+P_{X_{c1}}^TKQ+Q^TK^TP_{X_{c1}}<0$ 中，求解矩阵变量K。

注意到：
$A_0=\begin{bmatrix} A & 0 \\ 0 & 0 \end{bmatrix}、B_0=\begin{bmatrix} B_1\\ 0 \end{bmatrix}、C_0=\begin{bmatrix} C_1 & 0 \end{bmatrix}$
$\bar A=\begin{bmatrix} 0 & B_2 \\ I & 0 \end{bmatrix}、\bar C=\begin{bmatrix} 0 & I \\ C_2 & 0 \end{bmatrix}、\bar D_{12}=\begin{bmatrix} 0 & D_{12} \end{bmatrix}、\bar D_{21}=\begin{bmatrix} 0\\ D_{21} \end{bmatrix}$
$H_{X_{c1}}=\begin{bmatrix} A_0^TX_{c1}+X_{c1}A_0 & X_{c1}B_0 & C_0^T \\ B_0^TX_{c1} & -I & D_{11}^T \\ C_0 & D_{11} & -I \end{bmatrix}$
$P_{X_{c1}}=\begin{bmatrix} \bar B^TX_{c1} & 0 & \bar D_{12}^T \end{bmatrix}、Q=\begin{bmatrix} \bar C & \bar D_{21}^T & 0 \end{bmatrix}$

3、输出反馈 $\gamma$ -次优 $H_\infty$ 控制器

原线性定常系统存在一个输出反馈 $\gamma$ -次优 $H_\infty$ 控制器，当且仅当存在对称正定矩阵X和Y(Y也对称正定)，使得：**

$\begin{bmatrix} N_0 & 0 \\ 0 & I \end{bmatrix}^T\begin{bmatrix} A^TX+XA & XB_1 & C_1^T \\ B_1^TX & -\gamma I & D_{11}^T \\ C_1 & D_{11} & -\gamma I \end{bmatrix}\begin{bmatrix} N_0 & 0 \\ 0 & I \end{bmatrix}<0$
$\begin{bmatrix} N_c & 0 \\ 0 & I \end{bmatrix}^T\begin{bmatrix} AY+YA^T & YC_1^T & B_1 \\ C_1Y & -\gamma I & D_{11} \\ B_1^TC_1 & D_{11}^T & -\gamma I \end{bmatrix}\begin{bmatrix} N_c & 0 \\ 0 & I \end{bmatrix}<0$
$\begin{bmatrix} X & I \\ I & Y \end{bmatrix}\ge0$

4、输出反馈最优 $H_\infty$ 控制器

基于输出反馈 $\gamma$ -次优 $H_\infty$ 控制器的存在条件，建立这样一个优化问题：
$min~\rho\\s.t.~\begin{bmatrix} N_0 & 0 \\ 0 & I \end{bmatrix}^T\begin{bmatrix} A^TX+XA & XB_1 & C_1^T \\ B_1^TX & -\rho I & D_{11}^T \\ C_1 & D_{11} & -\rho I \end{bmatrix}\begin{bmatrix} N_0 & 0 \\ 0 & I \end{bmatrix}<0\\ \begin{bmatrix} N_c & 0 \\ 0 & I \end{bmatrix}^T\begin{bmatrix} AY+YA^T & YC_1^T & B_1 \\ C_1Y & -\rho I & D_{11} \\ B_1^TC_1 & D_{11}^T & -\rho I \end{bmatrix}\begin{bmatrix} N_c & 0 \\ 0 & I \end{bmatrix}<0\\ \begin{bmatrix} X & I \\ I & Y \end{bmatrix}\ge0$

通过LMI工具箱的求解器mincx可以求解系统的输出反馈最优 $H_\infty$ 控制器。

5、连续时间系统 $H_\infty$ 控制器综合问题求解器hinflmi

对于以下一阶系统：
$\dot x=w+2u\\z=x\\y=-x+w$
需要首先在MATLAB中建立系统，使用ltisys函数。
ltisys函数的基本用法是G=ltisys(A,B,C,D);

使用hinflmi函数可得到系统的最优 $H_\infty$ 控制器。
hinflmi函数的基本用法是==[gopt,K]=hinflmi(system,[p m])==，通过mincx来优化系统的 $H_\infty$ 性能指标，其中p是系统测量输出的个数，m是系统控制输入的个数，K是最优 $H_\infty$ 控制器系统矩阵，可通过ltiss函数得到其状态空间实现。

A=0;B1=1;B2=2;
C1=1;D11=0;D12=0;
C2=-1;D21=1;D22=0;
B=[B1 B2];C=[C1;C2];D=[D11,D12;D21,D22];
G=ltisys(A,B,C,D);
[gopt,K]=hinflmi(G,[1 1]);
[Ak,Bk,Ck,Dk]=ltiss(K)

可以得到系统的最优 $H_\infty$ 性能指标为：best objective value: 1.002517。

如果想计算满足 $H_\infty$ 性能 $\gamma<10$ 的一个输出反馈次优 $H_\infty$ 控制器，可以输入[gopt,K]=hinflmi(G,[1 1],10);

clsys=slft(G,K);	% 闭环系统clsys
spol(clsys);		% 返回闭环系统的极点，检验稳定性
norminf(clsys);		% 返回EE增益

四、状态反馈 $H_{\infty}$ 控制实例

1、控制器参数求解

clc;clear all
%% 某系统
A=[0  1       0       0;
   0 -0.0883  0.6293  0;
   0  0       0       1;
   0 -0.2357  27.8285 0] ;
B1=[0 2.3566  0 104.2027]';
B2=[0 0.8832  0 2.3566]';
C1=[0.064 0     0    0;
    0     1e-3  0    0;
    0     0     0.11 0;
    0     0     0    0.01;
    0     0     0    0];
D12=[0 0 0 0 0.01]';
D11=[0 0 0 0 0]';
C2=[1 0 0 0;
    0 0 1 0;
    0 0 0 0;
    0 0 0 0];
D21=[0 0 0 0]';
D22=[0 0 0 0]';
%% 状态反馈H无穷控制器
setlmis([])
X=lmivar(1,[4 1]);              % 对称正定矩阵X
W=lmivar(2,[1 4]);              % 矩阵W
lmiterm([1 1 1 X],A,1,'s');     % AX+(AX)'    11
lmiterm([1 1 1 W],B2,1,'s');    % B2W+(B2W)'  11
lmiterm([1 2 1 0],B1');         % B1'         21
lmiterm([1 2 2 0],-1);          % -I          22
lmiterm([1 3 1 X],C1,1);        % C1X         31
lmiterm([1 3 1 W],D12,1);       % D12W        31
lmiterm([1 3 2 0],D11);         % D11         32
lmiterm([1 3 3 0],-1);          % -I          33
lmiterm([-2 1 1 X],1,1);        % X>0	特别注意不能漏掉
lmisys=getlmis;
[tmin, xfeas]=feasp(lmisys);
XX1=dec2mat(lmisys,xfeas,X);
WW1=dec2mat(lmisys,xfeas,W);
K1=WW1*inv(XX1);
%% 状态反馈H无穷gamma-次优控制器 取gamma=2;
setlmis([])
X=lmivar(1,[4 1]);              % 对称正定矩阵X
W=lmivar(2,[1 4]);              % 矩阵W
lmiterm([1 1 1 X],A,1,'s');     % AX+(AX)'    11
lmiterm([1 1 1 W],B2,1,'s');    % B2W+(B2W)'  11
lmiterm([1 2 1 0],B1');         % B1'         21
lmiterm([1 2 2 0],-1);          % -I          22
lmiterm([1 3 1 X],C1,1);        % C1X         31
lmiterm([1 3 1 W],D12,1);       % D12W        31
lmiterm([1 3 2 0],D11);         % D11         32
lmiterm([1 3 3 0],-4);          % -4I         33
lmiterm([-2 1 1 X],1,1);        % X>0	特别注意不能漏掉
lmisys=getlmis;
[tmin, xfeas]=feasp(lmisys);
XX2=dec2mat(lmisys,xfeas,X);
WW2=dec2mat(lmisys,xfeas,W);
K2=WW2*(XX2)^-1;
%% 最优状态反馈H无穷控制器
setlmis([])
X=lmivar(1,[4 1]);              % 对称正定矩阵X
W=lmivar(2,[1 4]);              % 矩阵W
rho=lmivar(1,[1 1]);            % rho
lmiterm([1 1 1 X],A,1,'s');     % AX+(AX)'    11
lmiterm([1 1 1 W],B2,1,'s');    % B2W+(B2W)'  11
lmiterm([1 2 1 0],B1');         % B1'         21
lmiterm([1 2 2 0],-1);          % -I          22
lmiterm([1 3 1 X],C1,1);        % C1X         31
lmiterm([1 3 1 W],D12,1);       % D12W        31
lmiterm([1 3 2 0],D11);         % D11         32
lmiterm([1 3 3 rho],-1,1);      % -rhoI       33
lmiterm([-2 1 1 X],1,1);        % X>0
lmisys=getlmis;
n = decnbr(lmisys);             % 系统决策变量个数
c = zeros(n,1);                 % 确定向量c的维数
for j=1:n
     [r1j]=defcx(lmisys,j,rho);
      c(j)=trace(r1j);
end
%c=mat2dec(lmisys,zeros(4,4),zeros(1,4),eye(1))
[copt,xopt]=mincx(lmisys,c);
XX3=dec2mat(lmisys,xopt,X);
WW3=dec2mat(lmisys,xopt,W);
K3=WW3*(XX3)^-1;
rhoo=dec2mat(lmisys,xopt,rho);

2、仿真

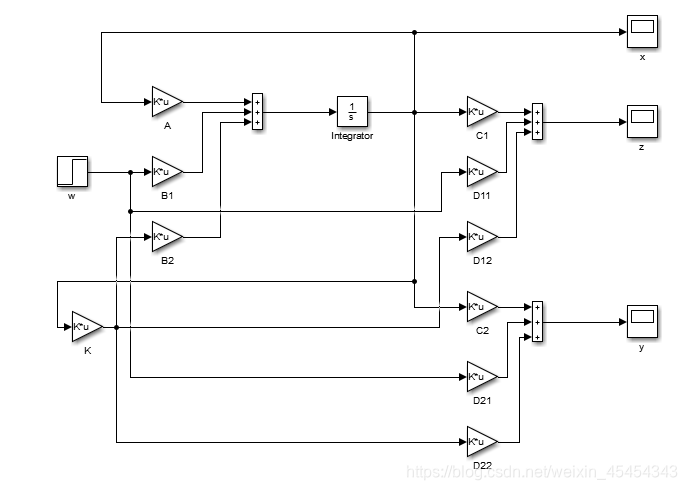
在这里插入图片描述
本文是作者在日常学习生活中所作，难免有遗漏或错误，遇到问题的读者请点击给我写信向我的邮箱反馈，不胜感激。

一饮丶一啄

关注

47
点赞
踩
227

收藏

觉得还不错? 一键收藏
13
评论
H无穷控制学习笔记——H无穷控制

一、H∞H_\inftyH∞控制总纲针对广义系统：其中，G(s)是一个线性定常系统，其状态空间描述为：x˙=Ax+B1w+B2uz=C1x+D11w+D12uy=C2x+D21w+D22u\dot x=Ax+B_1w+B_2u\\z=C_1x+D_{11}w+D_{12}u\\y=C_2x+D_{21}w+D_{22}ux˙=Ax+B1w+B2uz=C1x+D11w+D12uy=C2x+D21w+D22u其中，x∈Rnx\in R^nx∈Rn是状态向量，u∈Rmu\in R^mu∈R
复制链接

扫一扫