一、根轨迹法和频率响应法怎么用？
根轨迹法中的根轨迹指**开环系统的某一参数从零变化到无穷时，闭环系统传递函数的极点在s平面上变化的轨迹**(不考虑零极点相消)。
常规根轨迹法采用开环增益从零变化到无穷。
频率响应法使用开环传递函数推断闭环系统的相对稳定性。需要将系统转化为典型环节表示的形式，并通过幅值裕度和相角裕度调整比例环节K。
根据根轨迹的变化曲线，我们可取某一点的K值设计出具有期望性能的闭环系统。
二、控制器设计问题
若系统传递函数已知，需要设计PI控制器参数Kp和Ki，使闭环系统具有性能：
- 系统对阶跃输入响应无稳态误差，对斜坡输入响应稳态误差小于输入幅值的0.35；
- 系统阶跃响应调节时间小于等于3s。
控制系统结构如下图所示。
三、根轨迹法设计思路
整体系统开环传递函数为：
G
1
(
s
)
=
K
(
s
)
G
(
s
)
H
(
s
)
=
110
∗
1.24
K
p
(
s
+
K
i
/
K
p
)
(
s
+
5
)
s
(
s
2
+
460
s
+
550
)
G_1(s)=K(s)G(s)H(s)=\frac{110*1.24K_p(s+K_i/K_p)(s+5)}{s(s^2+460s+550)}
G1(s)=K(s)G(s)H(s)=s(s2+460s+550)110∗1.24Kp(s+Ki/Kp)(s+5)
其开环增益为
110
∗
1.24
K
p
110*1.24K_p
110∗1.24Kp，零点为
−
K
i
/
K
p
-K_i/K_p
−Ki/Kp、-5，极点为0、-1.19、-458。
1、根轨迹分析
绘制开环系统根轨迹图像如下：
(1)情况一： K i / K p < 0 K_i/K_p<0 Ki/Kp<0
此时闭环系统有一个极点始终在实半平面，系统对于任意开环增益都不稳定。
取
K
p
=
100
、
K
i
=
−
100
K_p=100、K_i=-100
Kp=100、Ki=−100和
K
p
=
1
、
K
i
=
−
1
K_p=1、K_i=-1
Kp=1、Ki=−1和
K
p
=
0.01
、
K
i
=
−
0.01
K_p=0.01、K_i=-0.01
Kp=0.01、Ki=−0.01仿真结果如下。
(2)情况二： 0 < K i / K p < 1.19 0<K_i/K_p<1.19 0<Ki/Kp<1.19(弱积分器)
此时闭环系统的闭环极点均位于负实轴上，对于任意开环增益都是稳定的，系统均为过阻尼系统，此时阶跃响应无超调。
取
K
p
=
100
、
K
i
=
100
K_p=100、K_i=100
Kp=100、Ki=100和
K
p
=
1
、
K
i
=
1
K_p=1、K_i=1
Kp=1、Ki=1和
K
p
=
0.1
、
K
i
=
0.1
K_p=0.1、K_i=0.1
Kp=0.1、Ki=0.1仿真结果如下。
此时
K
i
/
K
p
K_i/K_p
Ki/Kp均等于1，闭环零点位置不变，
K
p
K_p
Kp越大，开环增益越大，闭环主导极点越来越远离虚轴，系统阶跃响应越快。
取
K
p
=
1
、
K
i
=
0.1
K_p=1、K_i=0.1
Kp=1、Ki=0.1和
K
p
=
1
、
K
i
=
0.5
K_p=1、K_i=0.5
Kp=1、Ki=0.5和
K
p
=
1
、
K
i
=
1
K_p=1、K_i=1
Kp=1、Ki=1仿真结果如下。
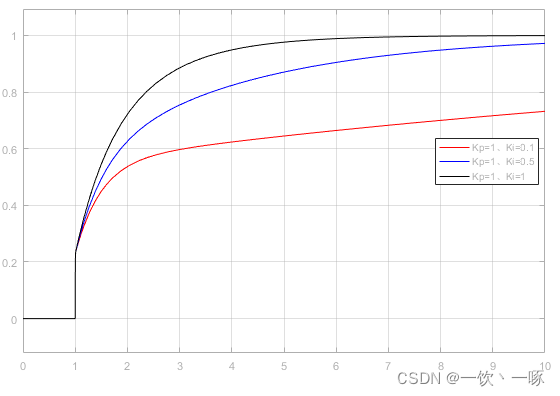此时
K
p
K_p
Kp不变，开环增益不变，但
K
i
/
K
p
K_i/K_p
Ki/Kp越来越大，闭环零点越来越远离虚轴，同样的开环增益闭环主导极点越来越远离虚轴，系统阶跃响应越快。
(3)情况三、四、五： 1.19 < K i / K p 1.19<K_i/K_p 1.19<Ki/Kp(强积分器)
此时任意开环增益系统都能稳定，但当开环增益在某一区间时，闭环极点为复数极点，系统为欠阻尼系统。
取
K
p
=
10
、
K
i
=
20
K_p=10、K_i=20
Kp=10、Ki=20和
K
p
=
1
、
K
i
=
2
K_p=1、K_i=2
Kp=1、Ki=2和
K
p
=
0.5
、
K
i
=
1
K_p=0.5、K_i=1
Kp=0.5、Ki=1仿真结果如下。
此时
K
i
/
K
p
K_i/K_p
Ki/Kp均等于2，闭环零点位置不变，
K
p
K_p
Kp越大，开环增益越大，闭环主导极点越来越远离虚轴，系统阶跃响应越快。
取 K p = 1 、 K i = 2 K_p=1、K_i=2 Kp=1、Ki=2和 K p = 1 、 K i = 10 K_p=1、K_i=10 Kp=1、Ki=10和 K p = 1 、 K i = 500 K_p=1、K_i=500 Kp=1、Ki=500仿真结果如下。
此时
K
p
K_p
Kp不变，开环增益不变，但
K
i
/
K
p
K_i/K_p
Ki/Kp越来越大，闭环零点越来越远离虚轴，同样的开环增益闭环主导极点越来越远离虚轴，系统阶跃响应越快。
因此Kp和Ki越大越好？高增益会放大噪声。需要选取合适地参数。
2、稳态误差需求
该系统在输入下，误差信号为：
E
(
s
)
=
R
(
s
)
1
+
K
(
s
)
G
(
s
)
H
(
s
)
E(s)=\frac{R(s)}{1+K(s)G(s)H(s)}
E(s)=1+K(s)G(s)H(s)R(s)
阶跃输入为
R
s
\frac{R}{s}
sR，稳态误差为：
e
s
s
(
∞
)
=
l
i
m
t
→
∞
e
(
t
)
=
l
i
m
s
→
0
s
E
(
s
)
=
0
e_ss(\infty)=lim_{t\to \infty}e(t)=lim_{s\to0}sE(s)=0
ess(∞)=limt→∞e(t)=lims→0sE(s)=0
斜坡输入为
R
s
2
\frac{R}{s^2}
s2R，稳态误差为：
e
s
s
(
∞
)
=
l
i
m
t
→
∞
e
(
t
)
=
l
i
m
s
→
0
s
E
(
s
)
=
0.7991
R
K
i
e_ss(\infty)=lim_{t\to \infty}e(t)=lim_{s\to0}sE(s)=0.7991\frac{R}{K_i}
ess(∞)=limt→∞e(t)=lims→0sE(s)=0.7991KiR
因此对于阶跃输入无稳态误差，对于斜坡输入必定存在稳态误差，
K
i
K_i
Ki绝对值越大，稳态误差越小,需要满足：
0.7991
/
K
i
≤
0.35
0.7991/K_i\le0.35
0.7991/Ki≤0.35，得到：
K
i
<
0
或
K
i
≥
2.29
K_i<0或K_i\ge2.29
Ki<0或Ki≥2.29。
四、频率特性
K
p
=
1
、
K
i
/
K
p
=
1
K_p=1、K_i/K_p=1
Kp=1、Ki/Kp=1
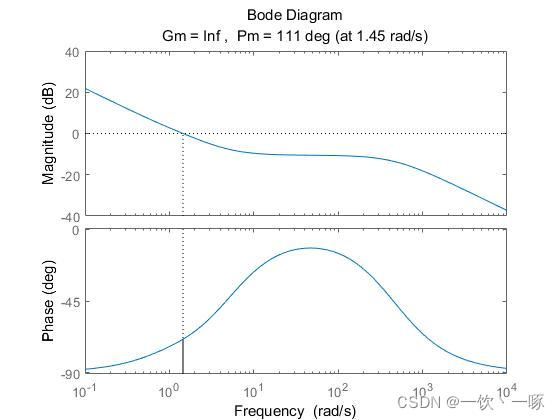
(参考书籍：自动控制原理第六版, 胡寿松)
扫一扫
1906
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
