OSQP 求解器教程

最新推荐文章于 2024-09-30 10:09:00 发布

kuan_li_lyg

最新推荐文章于 2024-09-30 10:09:00 发布

阅读量926

点赞数 28

文章标签：机器人人工智能开发语言自动驾驶 QP MPC OSQP

本文链接：https://blog.csdn.net/weixin_46300916/article/details/142155541

版权

系列文章目录

前言

OSQP 求解器文档
[请访问我们的 GitHub 讨论页面 (https://github.com/orgs/osqp/discussions)，了解与求解器相关的任何问题！

OSQP（运算符分割二次方程式程序）求解器是一个数值优化软件包，用于求解形式如下的凸二次规划

$\begin{aligned}&\mathrm{minimize}\quad\frac12x^TPx+q^Tx\\&\mathrm{subject~to}\quad l\leq Ax\leq u\end{aligned}$

其中 x 为优化变量，x 为半正定矩阵。半正定矩阵，是正定矩阵的推广。实对称矩阵A称为半正定的，如果二次型X'AX半正定，即对于任意不为0的实列向量X，都有X'AX≥0.

代码可在 GitHub 上获取。

引用 OSQP

如果您在工作中使用 OSQP，我们鼓励您

引用相关论文
在 GitHub github-star 上放一颗星

我们期待听到您使用 OSQP 的成功故事！请与我们分享。

功能特点

高效

        它使用基于 ADMM 的自定义一阶方法，只需在设置阶段进行一次矩阵因式分解。所有其他操作都非常简单。它还利用问题数据中的结构实现了定制的稀疏线性代数例程。

稳健性

        该算法在设置后绝对不需要除法，也不需要对问题数据做任何假设（问题只需要是凸的）。它只需运行即可！

检测初等/二元不可行问题*

        当问题是基本不可行或对偶不可行时，OSQP 会检测到它。它是首个基于一阶方法的 QP 求解器。

可嵌入

        它有一个简单的界面，可生成定制的可嵌入 C 代码，无需内存管理器。

无库

        无需外部库即可运行。

高效热启动

        可轻松热启动，并可缓存矩阵因式分解，从而极其高效地解决参数化问题。

接口

        它为 C、C++、Fortran、Julia、Matlab、Python、R、Ruby 和 Rust 提供了接口。

许可证

OSQP 采用 Apache 2.0 许可发布。

鸣谢

使用 OSQP 时，请注明 OSQP 开发团队。

接口开发

Nick Gould（卢瑟福阿普尔顿实验室）： Fortran和CUTEst接口

Ed Barnard（牛津大学）： Rust 界面

错误报告和支持

请通过 Github 问题跟踪器报告任何问题。我们欢迎所有类型的问题，包括错误报告、文档错字、功能请求等。

数值基准

这里提供了与其他求解器对比的数值基准。

一、求解器

1.1 问题陈述

OSQP 可求解如下形式的凸二次型规划（QPs）

$\begin{aligned}&\mathrm{minimize}&&\frac12x^TPx+q^Tx\\&\mathrm{subject~to}&&l\leq Ax\leq u\end{aligned}$

其中 $x\in\mathbf{R}^n$ 是优化变量。目标函数由半正定矩阵 $P\in\mathbf{S}_+^n$ 和向量 $q\in\mathbf{R}^n$ 定义。线性约束条件由矩阵 $A\in\mathbf{R}^{m\times n}$ 和向量 $l$ 及 $u$ 定义，因此对于所有 $i\in\{1,\ldots,m\}$ ， $l_i\in\mathbf{R}\cup\{-\infty\}$ 和 $u_i\in\mathbf{R}\cup\{+\infty\}$ 都是线性的。

1.2 算法

求解器运行以下 ADMM 算法（更多详情，请参阅引用 OSQP 部分的相关论文）：

$\begin{aligned} (x^{k+1},\nu^{k+1})& \leftarrow\text{solve linear system} \\ \tilde{z}^{k+1}& \leftarrow z^k+\rho^{-1}(\nu^{k+1}-y^k) \\ z^{k+1}& \leftarrow\Pi(\tilde{z}^k+\rho^{-1}y^k) \\ y^{k+1}& \leftarrow y^k+\rho(\tilde{z}^{k+1}-z^{k+1}) \end{aligned}$

其中， $\text{II}$ 是对超箱 $[l,u]$ 的投影。 $\rho$ 是 ADMM 步长。

1.2.1 线性系统求解

线性系统求解是算法的核心部分。可以采用直接或间接的方法。

使用直接线性系统求解器，我们可以用准无穷矩阵求解以下线性系统

$\begin{bmatrix}P+\sigma I&A^{T}\\A&-\rho^{-1}I\end{bmatrix}\begin{bmatrix}x^{k+1}\\\nu^{k+1}\end{bmatrix}=\begin{bmatrix}\sigma x^{k}-q\\z^{k}-\rho^{-1}y^{k}\end{bmatrix}.$

利用间接线性系统求解器，我们可以求解以下带有正定矩阵的线性系统

$\left(P+\sigma I+\rho A^TA\right)x^{k+1}=\sigma x^k-q+A^T(\rho z^k-y^k).$

OSQP 内核旨在支持不同的线性系统求解器。关于它们的安装，请参阅本节。要指定您最喜欢的线性系统求解器，请参阅本节。

1.2.2 收敛

每次迭代 $k$ 时，OSQP 都会产生一个包含 $x^k\in\mathbf{R}^n$ 和 $z^k,y^k\in\mathbf{R}^m$ 的元组 $(x^k,z^k,y^k)$ 。

与 $(x^k,z^k,y^k)$ 相关的原始残差和对偶残差为

$\begin{aligned}&r_{\mathrm{prim}}^k=Ax^k-z^k\\&r_{\mathrm{dual}}^k=Px^k+q+A^Ty^k.\end{aligned}$

互补松弛性是通过机器精度来实现的。如果问题可行，残差会随着 $k\to\infty$ 收敛为零。当 $r_{\mathrm{prim}}^k$ 和 $r_{\mathrm{dual}}^k$ 的规范值在指定的公差水平 $\epsilon_{\mathrm{prim}}>0$ 和 $\epsilon_{\mathrm{dual}}>0$ 范围内时，算法就会停止。

$\|r_{\mathrm{prim}}^k\|_\infty\leq\epsilon_{\mathrm{prim}},\quad\|r_{\mathrm{dual}}^k\|_\infty\leq\epsilon_{\mathrm{dual}}.$

我们将容差水平设定为

$\begin{aligned}&\epsilon_{\mathrm{prim}}=\epsilon_{\mathrm{abs}}+\epsilon_{\mathrm{rel}}\max\{\|Ax^k\|_\infty,\|z^k\|_\infty\}\\&\epsilon_{\mathrm{dual}}=\epsilon_{\mathrm{abs}}+\epsilon_{\mathrm{rel}}\max\{\|Px^k\|_\infty,\|A^Ty^k\|_\infty,\|q\|_\infty\}.\end{aligned}$

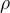1.2.3 $\rho$ 步长

为确保算法快速收敛，我们通过平衡残差来调整 $\rho$ 。在默认模式下，我们更新 $\rho$ 的跨度（即迭代次数）由时间测量确定。当迭代时间大于设置时间的某个分数（即自适应分数，adaptive_rho_fraction）时，我们会将当前的迭代次数设置为更新 $\rho$ 的时间间隔。更新过程如下

$\rho^{k+1}\leftarrow\rho^k\sqrt{\frac{\|r_\mathrm{prim}\|_\infty}{\|r_\mathrm{dual}\|_\infty}}.$

请注意，只有当 $\rho$ 与当前值有足够大的差异时，才会被更新。特别是当它比当前值大或小adaptive_rho_tolerance 倍时。

1.3 不可行问题

OSQP 能够检测问题是基本不可行还是对偶不可行。

1.3.1 基本不可行

当问题原始不可行时，算法会生成一个不可行证明，即一个向量 $v\in\mathbf{R}^m$ ，使得

$A^Tv=0,\quad u^Tv_++l^Tv_-<0,$

其中 $v_+=\max(v,0)$ 和 $v_-=\min(v,0)$ .

那么原始不可行性检验就是

$\left\|A^Tv\right\|_\infty\leq\epsilon_{\mathrm{prim_inf}},\quad u^Tv_++l^Tv_-<0.$

1.3.2 对偶不可行

当问题是对偶不可行时，OSQP 会生成一个向量 $s\in\mathbf{R}^n$ 作为对偶不可行的证明，即

因此，双重不可行性检验为

1.3.3 抛光

抛光是 OSQP 尝试计算高精度解的额外算法步骤。我们可以通过将 “抛光 ”设置为 1 来启用它。

抛光的工作原理是猜测最优时的活动约束条件，并求解一个额外的线性系统。如果猜测正确，OSQP 将返回一个高精度解决方案。否则，OSQP 将返回 ADMM 解决方案。抛光阶段的状态显示在 status_polish 信息中。

需要注意的是，如果线性系统求解器是直接求解，则抛光需要求解额外的线性系统，从而需要额外的因式分解。不过，该线性系统通常比 ADMM 迭代过程中求解的线性系统小得多。

如果公差 eps_abs 和 eps_rel 较小，抛光成功的几率就会增加。但是，低公差可能需要大量的迭代。

1.4 实现

OSQP 库提供了上述 ADMM 算法的 C 语言实现，还提供了若干高级语言的接口，使这些语言能够使用 OSQP 求解 QP。

此外，还有几种社区开发的 ADMM 算法实现。

Implementation	Language	Link
jaxopt.OSQP	JAX	jaxopt.github.io/stable/quadratic_programming.html#osqp
jOSQP	Java	github.com/quantego/josqp

请注意，这些实现可能不具备与 OSQP 库相同的应用程序接口或功能，如有任何问题或支持请求，请直接向 OSQP 库的作者提出。

二、示例

2.1 Demo

2.1.1 设置和求解

考虑以下 QP

$\begin{aligned}&\mathrm{minimize}\quad\frac12x^T\begin{bmatrix}4&1\\1&2\end{bmatrix}x+\begin{bmatrix}1\\1\end{bmatrix}^Tx\\&\mathrm{subject~to}\quad\begin{bmatrix}1\\0\\0\end{bmatrix}\leq\begin{bmatrix}1&1\\1&0\\0&1\end{bmatrix}x\leq\begin{bmatrix}1\\0.7\\0.7\end{bmatrix}\end{aligned}$

下面我们将展示如何用 Python、Matlab、Julia 和 C 语言来解决这个问题。

Python

import osqp
import numpy as np
from scipy import sparse

# Define problem data
P = sparse.csc_matrix([[4, 1], [1, 2]])
q = np.array([1, 1])
A = sparse.csc_matrix([[1, 1], [1, 0], [0, 1]])
l = np.array([1, 0, 0])
u = np.array([1, 0.7, 0.7])

# Create an OSQP object
prob = osqp.OSQP()

# Setup workspace and change alpha parameter
prob.setup(P, q, A, l, u, alpha=1.0)

# Solve problem
res = prob.solve()

2.1.2 更新向量

考虑下面的 QP

下面我们将展示如何设置和解决问题。然后，我们更新向量 $q$ 、 $l$ 和 $u$ ，并求解更新后的问题

$\begin{aligned}&\mathrm{minimize}\quad\frac12x^T\begin{bmatrix}4&1\\1&2\end{bmatrix}x+\begin{bmatrix}2\\3\end{bmatrix}^Tx\\&\mathrm{subject~to}\quad\begin{bmatrix}2\\-1\\-1\end{bmatrix}\leq\begin{bmatrix}1&1\\1&0\\0&1\end{bmatrix}x\leq\begin{bmatrix}2\\2.5\\2.5\end{bmatrix}\end{aligned}$

Python

import osqp
import numpy as np
from scipy import sparse

# Define problem data
P = sparse.csc_matrix([[4, 1], [1, 2]])
q = np.array([1, 1])
A = sparse.csc_matrix([[1, 1], [1, 0], [0, 1]])
l = np.array([1, 0, 0])
u = np.array([1, 0.7, 0.7])

# Create an OSQP object
prob = osqp.OSQP()

# Setup workspace
prob.setup(P, q, A, l, u)

# Solve problem
res = prob.solve()

# Update problem
q_new = np.array([2, 3])
l_new = np.array([2, -1, -1])
u_new = np.array([2, 2.5, 2.5])
prob.update(q=q_new, l=l_new, u=u_new)

# Solve updated problem
res = prob.solve()

2.1.3 更新矩阵

考虑以下 QP

下面我们将展示如何设置和解决问题。然后，我们更新矩阵 $\boldsymbol{P}$ 和 $\boldsymbol{A}$ ，并求解更新后的问题

$\begin{aligned}&\mathrm{minimize}\quad\frac{1}{2}x^{T}\begin{bmatrix}5&1.5\\1.5&1\end{bmatrix}x+\begin{bmatrix}1\\1\end{bmatrix}^{T}x\\&\mathrm{subject~to}\quad\begin{bmatrix}1\\0\\0\end{bmatrix}\leq\begin{bmatrix}1.2&1.1\\1.5&0\\0&0.8\end{bmatrix}x\leq\begin{bmatrix}1\\0.7\\0.7\end{bmatrix}\end{aligned}$

Python

import osqp
import numpy as np
from scipy import sparse

# Define problem data
P = sparse.csc_matrix([[4, 1], [1, 2]])
q = np.array([1, 1])
A = sparse.csc_matrix([[1, 1], [1, 0], [0, 1]])
l = np.array([1, 0, 0])
u = np.array([1, 0.7, 0.7])

# Create an OSQP object
prob = osqp.OSQP()

# Setup workspace
prob.setup(P, q, A, l, u)

# Solve problem
res = prob.solve()

# Update problem
# NB: Update only upper triangular part of P
P_new = sparse.csc_matrix([[5, 1.5], [1.5, 1]])
A_new = sparse.csc_matrix([[1.2, 1.1], [1.5, 0], [0, 0.8]])
prob.update(Px=sparse.triu(P_new).data, Ax=A_new.data)

# Solve updated problem
res = prob.solve()

2.2 应用

2.2.1 Huber 拟合

Huber 拟合或稳健最小二乘问题是在假设数据中存在异常值的情况下进行线性回归。拟合问题可写成

$\mathrm{minimize}\quad\sum_{i=1}^m\phi_{\mathrm{hub}}(a_i^Tx-b_i),$

胡贝尔惩罚函数 $\phi_\text{hub}:\mathbf{R}\to\mathbf{R}$ 的定义为

$\phi_{\mathrm{hub}}(u)=\left\{\begin{aligned}&u^2&|u|\leq1\\&(2|u|-1)&|u|>1\end{aligned}\right.$

问题的等价形式如下（更多详情请参见此处）

$\begin{gathered} \text{minimize} \: u^Tu+2\boldsymbol{1}^T(r+s) \\ \text{subject to} \: Ax-b-u=r-s \\ r\geq0 \\ s\geq0 \end{gathered}$

Python

import osqp
import numpy as np
import scipy as sp
from scipy import sparse

# Generate problem data
sp.random.seed(1)
n = 10
m = 100
Ad = sparse.random(m, n, density=0.5, format='csc')
x_true = np.random.randn(n) / np.sqrt(n)
ind95 = (np.random.rand(m) < 0.95).astype(float)
b = Ad@x_true + 0.5*np.random.randn(m) * ind95 \
    + 10.*np.random.rand(m) * (1. - ind95)

# OSQP data
Im = sparse.eye(m)
P = sparse.block_diag([sparse.csc_matrix((n, n)), 2*Im,
                       sparse.csc_matrix((2*m, 2*m))],
                       format='csc')
q = np.append(np.zeros(m+n), 2*np.ones(2*m))
A = sparse.bmat([[Ad,   -Im,   -Im,   Im],
                 [None,  None,  Im,   None],
                 [None,  None,  None, Im]], format='csc')
l = np.hstack([b, np.zeros(2*m)])
u = np.hstack([b, np.inf*np.ones(2*m)])

# Create an OSQP object
prob = osqp.OSQP()

# Setup workspace
prob.setup(P, q, A, l, u)

# Solve problem
res = prob.solve()

2.2.2 Lasso

Lasso 是一种众所周知的稀疏线性回归技术。它是通过在目标中添加一个 $\ell_{1}$ 正则化项得到的、

$\mathrm{minimize}\quad\frac12\|Ax-b\|_2^2+\gamma\|x\|_1$

其中 $x\in\mathbf{R}^n$ 为参数向量， $A\in\mathbf{R}^{m\times n}$ 为数据矩阵， $\gamma>0$ 为权重参数。问题的等价形式如下

$\begin{aligned}&\mathrm{minimize}&&\frac12y^Ty+\gamma\mathbf{1}^Tt\\&\mathrm{subject~to}&&y=Ax-b\\&&&-t\leq x\leq t\end{aligned}$

为了在解的稀疏性和线性拟合质量之间取得良好的平衡，我们求解了权重参数 $\gamma$ 变化的问题。
由于 $\gamma$ 只出现在目标函数的线性部分，因此我们可以重复使用矩阵因式分解并启用暖起始，以减少计算时间。

Python

import osqp
import numpy as np
import scipy as sp
from scipy import sparse

# Generate problem data
sp.random.seed(1)
n = 10
m = 1000
Ad = sparse.random(m, n, density=0.5)
x_true = (np.random.rand(n) > 0.8).astype(float) * np.random.randn(n) / np.sqrt(n)
b = Ad@x_true + 0.5*np.random.randn(m)
gammas = np.linspace(1, 10, 11)

# Auxiliary data
In = sparse.eye(n)
Im = sparse.eye(m)
On = sparse.csc_matrix((n, n))

# OSQP data
P = sparse.block_diag([On, Im, On], format='csc')
q = np.zeros(2*n + m)
A = sparse.bmat([[Ad, -Im,    None],
                 [In,  None, -In],
                 [In,  None,  In]], format='csc')
l = np.hstack([b, -np.inf * np.ones(n), np.zeros(n)])
u = np.hstack([b, np.zeros(n), np.inf * np.ones(n)])

# Create an OSQP object
prob = osqp.OSQP()

# Setup workspace
prob.setup(P, q, A, l, u, warm_starting=True)

# Solve problem for different values of gamma parameter
for gamma in gammas:
    # Update linear cost
    q_new = np.hstack([np.zeros(n+m), gamma*np.ones(n)])
    prob.update(q=q_new)

    # Solve
    res = prob.solve()

2.2.3 最小二乘法

考虑下面的约束最小二乘问题

$\begin{aligned}&\mathrm{minimize}&&\frac12\|Ax-b\|_2^2\\&\mathrm{subject~to}&&0\leq x\leq1\end{aligned}$

问题的等价形式如下

$\begin{array}{ll}\mathrm{minimize}&\frac12y^Ty\\\mathrm{subject~to}&y=Ax-b\\&0\leq x\leq1\end{array}$

Python

import osqp
import numpy as np
import scipy as sp
from scipy import sparse

# Generate problem data
sp.random.seed(1)
m = 30
n = 20
Ad = sparse.random(m, n, density=0.7, format='csc')
b = np.random.randn(m)

# OSQP data
P = sparse.block_diag([sparse.csc_matrix((n, n)), sparse.eye(m)], format='csc')
q = np.zeros(n+m)
A = sparse.bmat([[Ad,            -sparse.eye(m)],
                 [sparse.eye(n),  None]], format='csc')
l = np.hstack([b, np.zeros(n)])
u = np.hstack([b, np.ones(n)])

# Create an OSQP object
prob = osqp.OSQP()

# Setup workspace
prob.setup(P, q, A, l, u)

# Solve problem
res = prob.solve()

2.2.4 模型预测控制 (MPC)

我们考虑的问题是控制线性时变动态系统达到某个参考状态 $x_r\in\mathbf{R}^{n_x}$ 。为此，我们使用受约束线性二次型 MPC，在每个时间步求解以下有限视距最优控制问题

$\begin{aligned} \text{minimize} (x_N-x_r)^TQ_N(x_N-x_r)+\sum_{k=0}^{N-1}(x_k-x_r)^TQ(x_k-x_r)+u_k^TRu_k \\ \text{subject to}\: & x_{k+1}=Ax_k+Bu_k \\ &x_{\min}\leq x_k\leq x_{\max} \\ &u_{\min}\leq u_k\leq u_{\max} \\ &x_0=\bar{x} \end{aligned}$

Python

import osqp
import numpy as np
import scipy as sp
from scipy import sparse

# Discrete time model of a quadcopter
Ad = sparse.csc_matrix([
  [1.,      0.,     0., 0., 0., 0., 0.1,     0.,     0.,  0.,     0.,     0.    ],
  [0.,      1.,     0., 0., 0., 0., 0.,      0.1,    0.,  0.,     0.,     0.    ],
  [0.,      0.,     1., 0., 0., 0., 0.,      0.,     0.1, 0.,     0.,     0.    ],
  [0.0488,  0.,     0., 1., 0., 0., 0.0016,  0.,     0.,  0.0992, 0.,     0.    ],
  [0.,     -0.0488, 0., 0., 1., 0., 0.,     -0.0016, 0.,  0.,     0.0992, 0.    ],
  [0.,      0.,     0., 0., 0., 1., 0.,      0.,     0.,  0.,     0.,     0.0992],
  [0.,      0.,     0., 0., 0., 0., 1.,      0.,     0.,  0.,     0.,     0.    ],
  [0.,      0.,     0., 0., 0., 0., 0.,      1.,     0.,  0.,     0.,     0.    ],
  [0.,      0.,     0., 0., 0., 0., 0.,      0.,     1.,  0.,     0.,     0.    ],
  [0.9734,  0.,     0., 0., 0., 0., 0.0488,  0.,     0.,  0.9846, 0.,     0.    ],
  [0.,     -0.9734, 0., 0., 0., 0., 0.,     -0.0488, 0.,  0.,     0.9846, 0.    ],
  [0.,      0.,     0., 0., 0., 0., 0.,      0.,     0.,  0.,     0.,     0.9846]
])
Bd = sparse.csc_matrix([
  [0.,      -0.0726,  0.,     0.0726],
  [-0.0726,  0.,      0.0726, 0.    ],
  [-0.0152,  0.0152, -0.0152, 0.0152],
  [-0.,     -0.0006, -0.,     0.0006],
  [0.0006,   0.,     -0.0006, 0.0000],
  [0.0106,   0.0106,  0.0106, 0.0106],
  [0,       -1.4512,  0.,     1.4512],
  [-1.4512,  0.,      1.4512, 0.    ],
  [-0.3049,  0.3049, -0.3049, 0.3049],
  [-0.,     -0.0236,  0.,     0.0236],
  [0.0236,   0.,     -0.0236, 0.    ],
  [0.2107,   0.2107,  0.2107, 0.2107]])
[nx, nu] = Bd.shape

# Constraints
u0 = 10.5916
umin = np.array([9.6, 9.6, 9.6, 9.6]) - u0
umax = np.array([13., 13., 13., 13.]) - u0
xmin = np.array([-np.pi/6,-np.pi/6,-np.inf,-np.inf,-np.inf,-1.,
                 -np.inf,-np.inf,-np.inf,-np.inf,-np.inf,-np.inf])
xmax = np.array([ np.pi/6, np.pi/6, np.inf, np.inf, np.inf, np.inf,
                  np.inf, np.inf, np.inf, np.inf, np.inf, np.inf])

# Objective function
Q = sparse.diags([0., 0., 10., 10., 10., 10., 0., 0., 0., 5., 5., 5.])
QN = Q
R = 0.1*sparse.eye(4)

# Initial and reference states
x0 = np.zeros(12)
xr = np.array([0.,0.,1.,0.,0.,0.,0.,0.,0.,0.,0.,0.])

# Prediction horizon
N = 10

# Cast MPC problem to a QP: x = (x(0),x(1),...,x(N),u(0),...,u(N-1))
# - quadratic objective
P = sparse.block_diag([sparse.kron(sparse.eye(N), Q), QN,
                       sparse.kron(sparse.eye(N), R)], format='csc')
# - linear objective
q = np.hstack([np.kron(np.ones(N), -Q@xr), -QN@xr, np.zeros(N*nu)])
# - linear dynamics
Ax = sparse.kron(sparse.eye(N+1),-sparse.eye(nx)) + sparse.kron(sparse.eye(N+1, k=-1), Ad)
Bu = sparse.kron(sparse.vstack([sparse.csc_matrix((1, N)), sparse.eye(N)]), Bd)
Aeq = sparse.hstack([Ax, Bu])
leq = np.hstack([-x0, np.zeros(N*nx)])
ueq = leq
# - input and state constraints
Aineq = sparse.eye((N+1)*nx + N*nu)
lineq = np.hstack([np.kron(np.ones(N+1), xmin), np.kron(np.ones(N), umin)])
uineq = np.hstack([np.kron(np.ones(N+1), xmax), np.kron(np.ones(N), umax)])
# - OSQP constraints
A = sparse.vstack([Aeq, Aineq], format='csc')
l = np.hstack([leq, lineq])
u = np.hstack([ueq, uineq])

# Create an OSQP object
prob = osqp.OSQP()

# Setup workspace
prob.setup(P, q, A, l, u, warm_starting=True)

# Simulate in closed loop
nsim = 15
for i in range(nsim):
    # Solve
    res = prob.solve()

    # Check solver status
    if res.info.status != 'solved':
        raise ValueError('OSQP did not solve the problem!')

    # Apply first control input to the plant
    ctrl = res.x[-N*nu:-(N-1)*nu]
    x0 = Ad@x0 + Bd@ctrl

    # Update initial state
    l[:nx] = -x0
    u[:nx] = -x0
    prob.update(l=l, u=u)