文章探讨了逆运动学问题，即如何根据工具坐标系相对于固定坐标系的期望位置和姿态来确定六自由度机械臂的关节角。讨论了解的存在性和数量，指出解的数量依赖于关节数量、连杆参数及关节运动范围。文中以三轴相交的Pieper解法为例，详述了一个六关节机械臂在特定任务中的关节角计算过程，包括MDH建模和通过手臂计算任务点的齐次变换矩阵。
逆运动学：已知工具坐标系相对于固定坐标系的期望位置和姿态，求满足期望要求的关节角。
1.解的存在性
工作空间分为灵巧工作空间和可达工作区间。前者指机器人的末端执行器能够从各个方向到达的空间区域，即可以从任意方向到达灵巧工作空间的每一个点。后者指至少从一个方向上有一个方位可以达到的空间。显然，灵巧工作空间十可达工作空间的子集。
解的个数不仅取决于操作臂的关节数量，它还是连杆参数(对于旋转关节操作臂来说为
α
i
\alpha_{i}
αi、
a
i
a_{i}
ai、
d
i
d_{i}
di)和关节运动范围的函数。通常，连杆的非零参数越多，到达某一特定目标的方式也越多。以一个具有六个旋转关节的操作臂为例：
具有六个旋转关节的操作臂存在封闭解的充分条件是相邻的三根关节轴相交于一点。
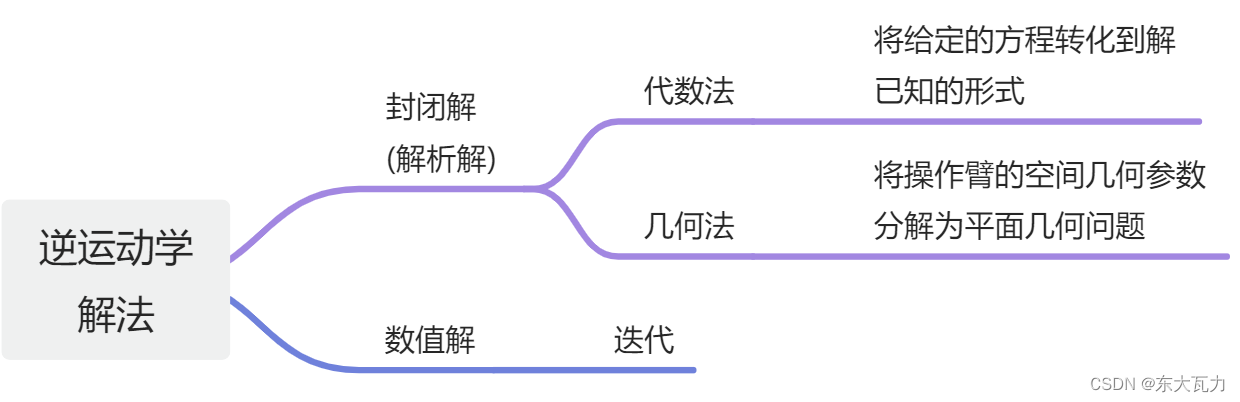
2.以三轴相交的Pieper解法为例
一个六自由度的(RRRRRR)机械臂要以如图所示位姿夹住杯子，任务起始点为C，求此时机械臂六个关节角。
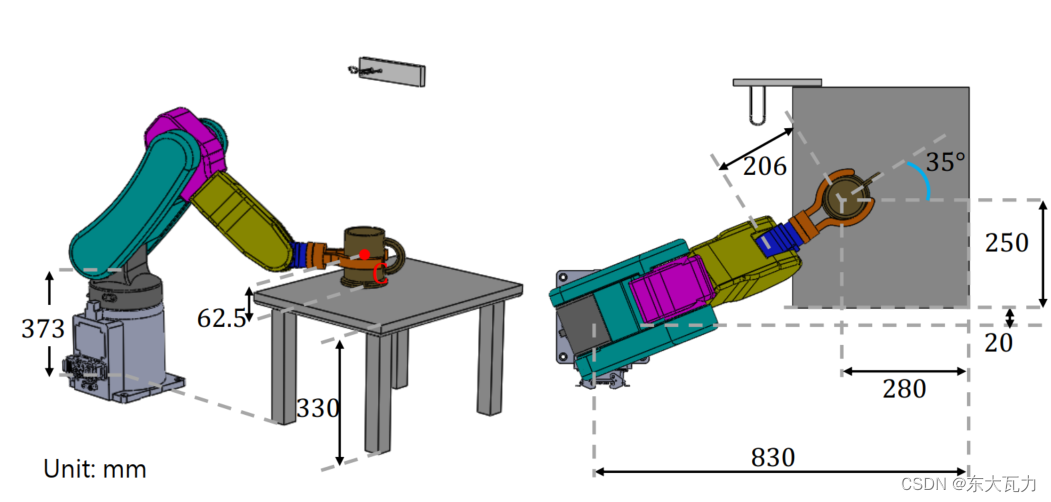
(1)MDH建模
（2）不经手臂计算任务点C相对于世界坐标系下的齐次变换矩阵
（3）经手臂计算任务点C相对于世界坐标系下的齐次变换矩阵
（4）求
θ
1
\theta_{1}
θ1、
θ
2
\theta_{2}
θ2、
θ
3
\theta_{3}
θ3
（4）求
θ
4
\theta_{4}
θ4、
θ
5
\theta_{5}
θ5、
θ
6
\theta_{6}
θ6
所以其中一种解可为：
3.参考
[1]约翰 J. 克雷格(John J. Craig)著的机
器人学导论，第四版；
[2]台湾大学-机器人学之运动学—林沛群；
扫一扫
3万+
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
