【自学】——动力学建模

Robotics Notes

拉格朗日动力学模型

1. 简介：

拉格朗日动力学的基础是系统能量对系统变量及时间的变分。

对于复杂系统的分析上其要比“牛顿-欧拉”简单。

2. 建模步骤：

1）选择广义坐标

待写

2）计算拉格朗日函数：

首先，定义系统的动能为$K$，势能为$P$，然后拉格朗日函数定义为：

$L=K-P$

对于机器鱼而言，由于重力$G$等于其浮力$B$，因此总势能$P=0$

3）利用Euler-Lagrange方程写出运动方程

定义$F_i$为产生线运动的所有外力之和，定义$T_i$为产生转动的所有外力矩之和，则根据Euler-Lagrange方程可得：

$\left[\begin{array}{c}{F}_i\\ T_i\end{array}\right]=\frac{d}{dt}(\frac{\partial L}{\partial {\dot{q}}_i})-\frac{\partial L}{\partial q_i}$

3. 后续分析

3.1 雅可比矩阵（Jacobian Matrix）

雅可比矩阵源自于关节微分运动，主要解决的是：“如何通过各关节的运动变化求出未端的广义速度”，即Jacobian Matrix反映的是：关节变化$\Delta Q_i$与末端变化$\Delta X$的关系。

原理上，可以从$X=f(q)$上推导，即对$X$的每一项进行全微分，有：

$\begin{array}{rl}& \Delta x_1=\frac{\partial f_1}{\partial q_1}\cdot \Delta q_1+\frac{\partial f_1}{\partial q_2}\cdot \Delta q_2+\cdots +\frac{\partial f_1}{\partial q_n}\cdot \Delta q_n\\ & \Delta x_2=\frac{\partial f_2}{\partial q_1}\cdot \Delta q_1+\frac{\partial f_2}{\partial q_2}\cdot \Delta q_2+\cdots +\frac{\partial f_2}{\partial q_n}\cdot \Delta q_n\\ & \\ & ...\\ & \\ & \Delta x_m=\frac{\partial f_m}{\partial q_1}\cdot \Delta q_1+\frac{\partial f_m}{\partial q_2}\cdot \Delta q_2+\cdots +\frac{\partial f_m}{\partial q_n}\cdot \Delta q_n\end{array}$

写成矩阵的形式，可表示为：

$\Delta \mathrm{X}=\left[\begin{array}{cccc}\frac{\partial f_1}{\partial q_1}& \frac{\partial f_1}{\partial q_2}& \cdots & \frac{\partial f_1}{\partial q_n}\\ \frac{\partial f_2}{\partial q_1}& \frac{\partial f_2}{\partial q_2}& \cdots & \frac{\partial f_2}{\partial q_n}\\ ⋮& ⋮& \ddots & ⋮\\ \frac{\partial f_m}{\partial q_1}& \frac{\partial f_m}{\partial q_2}& \cdots & \frac{\partial f_m}{\partial q_n}\end{array}\right]\Delta \mathrm{Q}=J\Delta Q$

其中，可以看出：

① 矩阵的行数 = $X$的项数 = 末端自由度的数量

② 矩阵的列数 = 广义坐标$Q$维数 = 关节数

3.1.1 求解过程

① 计算连杆间的齐次变换矩阵：${}^{i-1}{T}_i=\left[\begin{array}{cccc}n& o& a& p\end{array}\right]$

② 计算末端到前述各连杆的变换矩阵：${}^0{T}_6{,}^1{T}_6,...{,}^5{T}_6$

③ 由坐标系{T}和基坐标系间微分运动的坐标变换关系，计算$T_J$：

${}^{T}D=\left[\begin{array}{cccccc}{\mathrm{n}}_{\mathrm{x}}& {\mathrm{n}}_{\mathrm{y}}& {\mathrm{a}}_{\mathrm{x}}& {\left(\mathrm{p}\times \mathrm{n}\right)}_{\mathrm{x}}& {\left(\mathrm{p}\times \mathrm{n}\right)}_{\mathrm{y}}& {\left(\mathrm{p}\times \mathrm{n}\right)}_{\mathrm{z}}\\ {\mathrm{o}}_{\mathrm{x}}& {\mathrm{o}}_{\mathrm{y}}& {\mathrm{o}}_{\mathrm{z}}& {\left(\mathrm{p}\times 0\right)}_{\mathrm{x}}& {\left(\mathrm{p}\times \mathrm{o}\right)}_{\mathrm{y}}& {\left(\mathrm{p}\times \mathrm{o}\right)}_{\mathrm{z}}\\ {\mathrm{a}}_{\mathrm{x}}& {\mathrm{a}}_{\mathrm{y}}& {\mathrm{a}}_{\mathrm{z}}& {\left(\mathrm{p}\times \mathrm{a}\right)}_{\mathrm{x}}& {\left(\mathrm{p}\times \mathrm{a}\right)}_{\mathrm{y}}& {\left(\mathrm{p}\times \mathrm{a}\right)}_{\mathrm{z}}\\ 0& 0& 0& {\mathrm{n}}_{\mathrm{x}}& {\mathrm{n}}_{\mathrm{y}}& {\mathrm{a}}_{\mathrm{x}}\\ 0& 0& 0& {\mathrm{o}}_{\mathrm{x}}& {\mathrm{o}}_{\mathrm{y}}& {\mathrm{o}}_{\mathrm{z}}\\ 0& 0& 0& {\mathrm{a}}_{\mathrm{x}}& {\mathrm{a}}_{\mathrm{y}}& {\mathrm{a}}_{\mathrm{z}}\end{array}\right]D=T_{J}D$

${}^{T}D=\left[\begin{array}{ccc}{R}^T& & -R^{T}S(p)\\ 0& & R^T\end{array}\right]D$

其中，反对称矩阵$S(p)$定义为：

$\mathrm{S}(\mathrm{p})=\left[\begin{array}{ccc}0& -p_z& p_y\\ p_z& 0& p_x\\ -p_y& p_x& 0\end{array}\right]$

④ 写出雅可比矩阵，原则为：

若关节$i$为直线运动，则取$T_J$的第3列作为J的第$i$列；
若关节$i$为旋转运动，则取$T_J$的第6列作为J的第$i$列；

3.1.2 示例

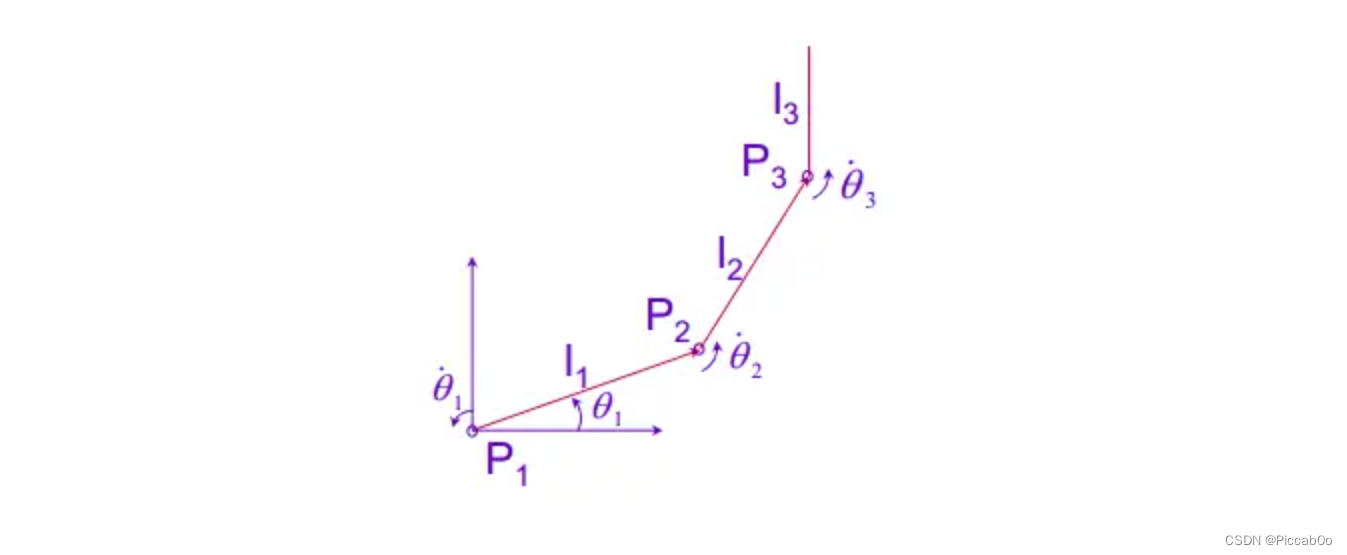
线速度累加


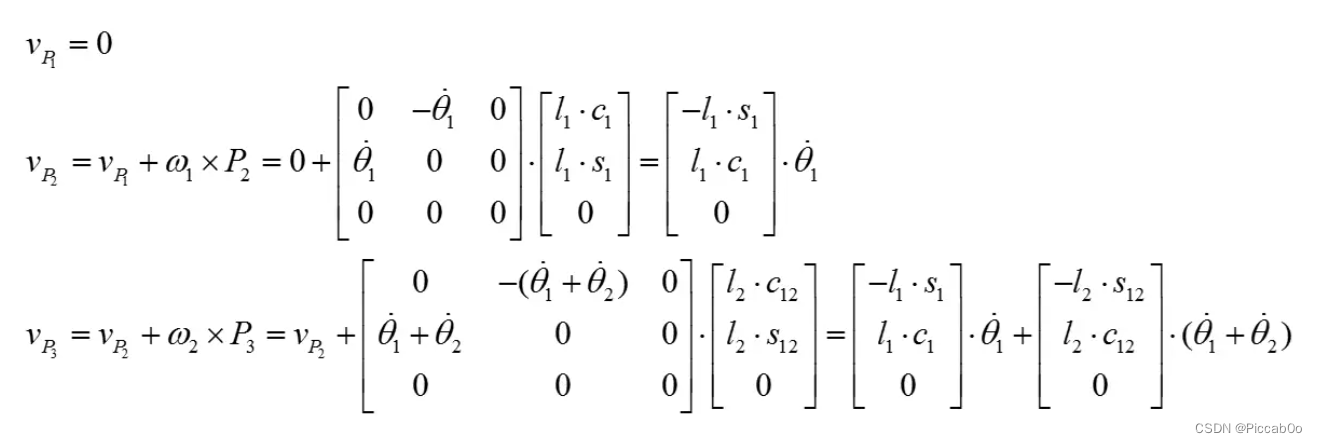
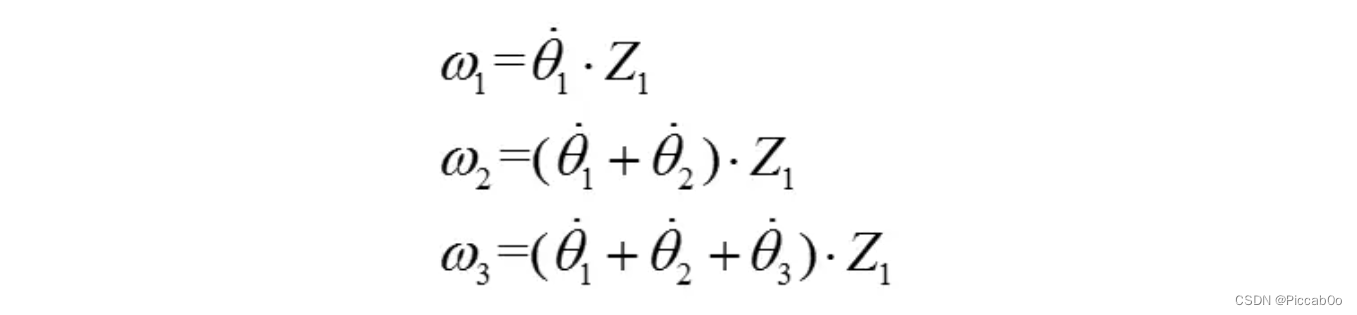
则：

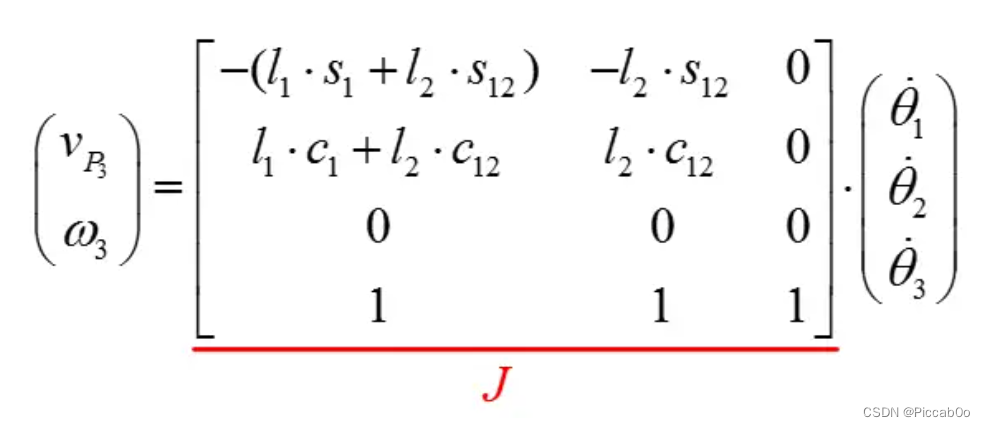
3.1.3 应用1——静力变换

雅可比矩阵跟机器人的构型有关，机器人的构型发生变化，雅可比矩阵也会发生变化。所以为了实时求得关节力矩，需要实时重新计算雅可比矩阵。

如果已知任一坐标系$B$相对于参考坐标系的齐次变换矩阵：

$T=\left[\begin{array}{cccc}n& o& a& p\end{array}\right]$

若再有表用在物体上相对于参考坐标系的力：

$F=\left[\begin{array}{c}f\\ m\end{array}\right]$

则可以不通过雅可比矩阵得到该力在坐标系$B$下等效的力和力矩：

$\begin{array}{rl}& {}^B{f}_x=n\cdot f\\ & {}^B{f}_{\gamma }=o\cdot f\\ & {}^B{f}_z=a\cdot f\\ & {}^B{m}_x=n\cdot [(f\times p)+m]\\ & {}^B{m}_{\gamma }=\mathbf{o}\cdot [(\mathbf{f}\times \mathbf{p})+\mathbf{m}]\\ & {}^B{m}_z=a\cdot [(f\times p)+m]\end{array}$