D触发器和16进制计数器设计Verilog代码Quartus仿真

名称：D触发器和16进制计数器设计Verilog代码Quartus仿真（文末获取）

软件：Quartus

语言：Verilog

代码功能：

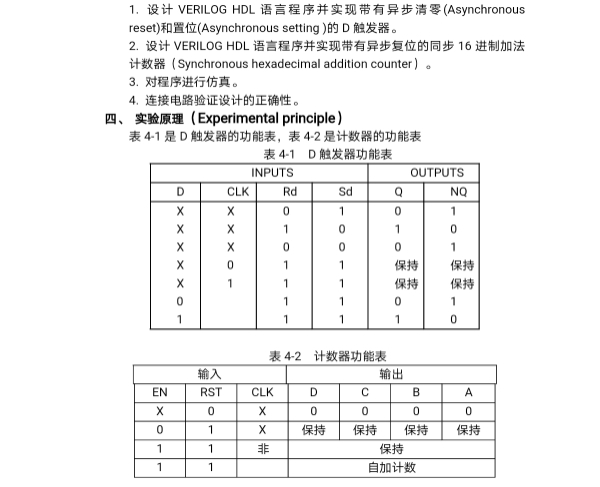
1.设计 VERILOG HDL语言程序并实现带有异步清零( Asynchronouseset)和置位( Asynchronous setting)的D触发器

2.设计 VERILOG HDL语言程序井实现带有异步复位的同步16进制加法

计数器( Synchronous hexadecimal addition counter)

3,对程序进行仿真

4.连接电路验证设计的正确性

 

   

1、工程文件

2、程序文件

3、程序编译

4、RTL图

5、仿真图

1、工程文件

2、程序文件

3、程序编译

4、RTL图

5、仿真图

部分代码展示:

//异步复位的同步16进制加法计数器
module cnt(
input CLK,//时钟
input RST,//异步复位
input EN,//使能
output A,B,C,D //4位输出
);
reg [3:0] count;
always@(posedge CLK or negedge RST)
if(!RST)
count<=4'd0;//异步复位
else if(EN)//高电平使能
count<=count+4'd1;//自加
assign A=count[0];//计数器第0位
assign B=count[1];//计数器第1位
assign C=count[2];//计数器第2位

源代码

点击下方的公众号卡片获取