3D空间中射线与轴向包围盒AABB的交叉检测算法

引言

            在上一节中，我讲述了如何实现射线与三角形的交叉检测算法。但是，我们应该知道，在游戏开发中，一个模型有很多的三角形构成，如果要对所有的物体，所有的三角形进行这种检测，就算现在的计算机运算能力，也是无法高效的完成。所以，我们需要通过其他的手段来提早剔除一些不可能发生交叉的物体，这种早退的思想，大量的运用在3D游戏技术中。在本篇文章中，我将像大家讲述如何实现射线与轴向包围盒AABB的交叉检测。如果读者不明白什么是轴向包围盒，请看这篇文章。

Ray-AABB交叉检测算法

            现如今，有很多的Ray-AABB交叉检测算法，这里主要讲述一种称之为"Slabs method"的交叉检测算法。

            在3D空间中，我们先确定正对着射线的三个面，也就是说，我们可以通过某种方式将AABB相对于射线Ray的背面给忽略掉，从而确定三个候选的面。这三个候选的面，就是有可能和射线Ray发生交叉的最近的面。同时，我们还需要知道一个事实：当射线与这三个候选面中的一个发生交叉之后，射线Ray的原点到这个面的距离要比到其他几个面的距离要长。

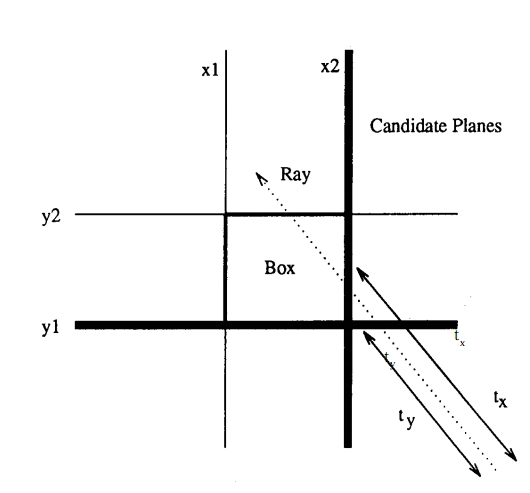
            如果对于上面的事实不是很清楚的话，我们来看下图：

             在上图中，我们的射线在右下角，向左上角发射。所以，候选面就是y1面，和x2面(这里由于讲述的方便，使用2D图形来表示)。ty是射线到y1面的距离，tx是射线到x2的距离。从上图中可以看出tx > ty， 而射线与x2平面相交叉。

             通过上图，大家就应该明白了，上面那个事实的含义了。这个算法也就是基于此等事实来实现的。

              我们知道射线的公式为R(t) = O + t * D，上图中所说的射线到某个面的距离，实际上就是射线原点到射线与该平面的交叉点的距离，而这个距离，刚好就是我们将平面方程带入R(t) = O + t * D中，计算出来的t的值。所以ÿ