一区新风向：PINN+贝叶斯！！

最新推荐文章于 2025-02-10 14:45:25 发布

人工智能学起来

最新推荐文章于 2025-02-10 14:45:25 发布

阅读量746

点赞数 7

文章标签：人工智能深度学习

本文链接：https://blog.csdn.net/2401_88190197/article/details/143956978

版权

今天给大家推荐一个好发一区TOP的思路：PINN+贝叶斯！

贝叶斯的引入，为PINN的改进提供了新视角，在提高预测准确性、可靠性、计算效率和规避过拟合方面，展现了强大的优势。比如模型BPIELM便在准确性提高30％的同时，训练速度提高70倍！

主要在于：PINN利用深度学习的强大计算能力，能够高效地处理复杂的数据集和模型结构，而贝叶斯方法则提供了有效的模型选择和参数估计手段，两者相辅相成。尤为特殊的是，该结合能在不确定性条件下提供更丰富的信息输出，如后验标准差等，使模型更好地处理复杂数据集和场景，这是其他方法做不到的。

此外，该思路目前还在蓝海期，创新空间很大！为让大家能紧跟领域前沿，找到更多idea启发，我给大家准备了8种创新思路及开源代码！

论文原文+开源代码需要的同学看文末

论文：Bayesian Physics-Informed Extreme Learning Machine for Forward and Inverse PDE Problems with Noisy Data

内容

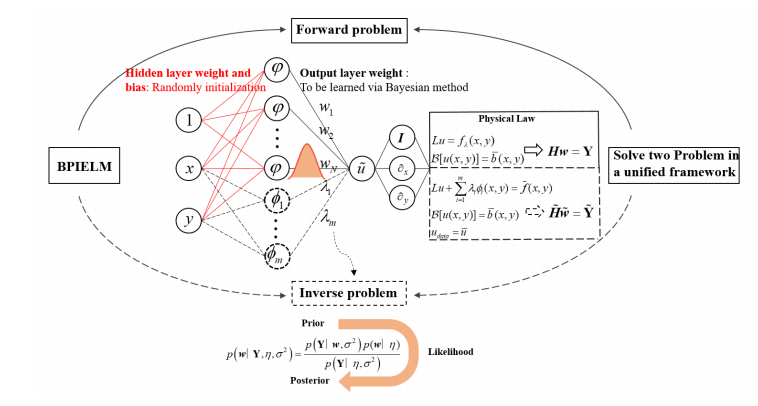
该论文介绍了一种名为贝叶斯物理信息极学习机（BPIELM）的新方法，用于解决带有噪声数据的正向和逆向偏微分方程（PDE）问题。BPIELM结合了极学习机（ELM）和贝叶斯方法，通过引入先验概率分布并使用贝叶斯方法估计参数的后验分布来量化噪声数据带来的不确定性。与物理信息神经网络（PINN）和极学习机（PIELM）相比，BPIELM在预测准确性和计算成本方面表现出显著优势，尤其是在噪声场景下。

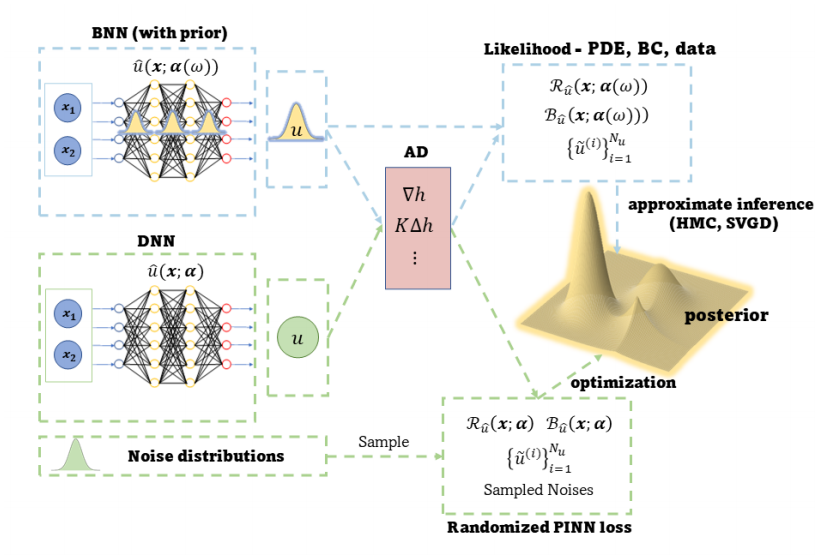
论文：Randomized Physics-Informed Neural Networks for Bayesian Data Assimilation

内容

该论文提出了一种名为随机化物理信息神经网络（rPINN）的方法，用于在存在噪声数据的逆偏微分方程（PDE）问题中进行不确定性量化。该方法通过在物理信息神经网络（PINN）的损失函数中引入随机噪声，并通过对不同噪声实现的最小化问题的解来近似后验分布，从而克服了传统贝叶斯PINN（BPINN）方法在非线性逆PDE问题中汉密尔顿蒙特卡洛（HMC）收敛失败的问题。

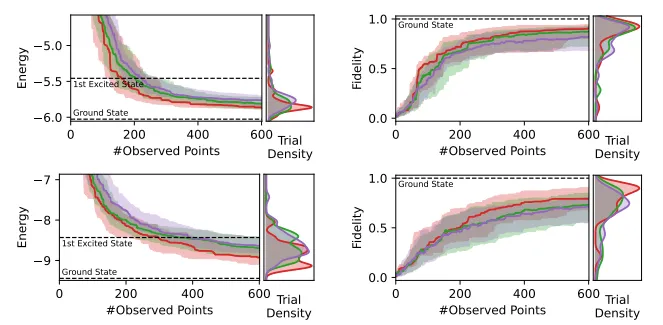
论文：Physics-Informed Bayesian Optimization of Variational Quantum Circuits

内容

该论文提出了一种新的贝叶斯优化方法，用于变分量子电路（VQE）的物理信息贝叶斯优化。该方法通过在VQE的目标函数中引入一个与量子电路结构相匹配的VQE核，显著降低了后验不确定性。同时，文章提出了一种名为EMICoRe的新型采集函数，能够主动利用VQE核的归纳偏差，将预测不确定性低的区域视为间接“观测”到的区域。这种方法仅需要在搜索域中的三个点进行观测，就能确定整个一维子空间中的完整目标函数。