【欠驱动机械系统的部分反馈线性化】在部分反馈线性化控制下，两连杆欠驱动机器人性能的仿真研究（Matlab代码实现）

最新推荐文章于 2025-04-23 17:09:44 发布

长安程序猿

最新推荐文章于 2025-04-23 17:09:44 发布

阅读量404

点赞数 17

文章标签：机器人 matlab 前端

本文链接：https://blog.csdn.net/Yan_she_He/article/details/147407810

版权

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

⛳️赠与读者

💥1 概述

部分反馈线性化控制下两连杆欠驱动机器人性能仿真研究

1. 欠驱动机械系统与两连杆结构特点

2. 部分反馈线性化（PFL）控制原理

3. 两连杆欠驱动机器人动力学建模

4. 部分反馈线性化控制实现案例

5. 性能评估指标与方法

6. 挑战与未来方向

7. 结论

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码、文章下载

⛳️赠与读者

👨‍💻做科研，涉及到一个深在的思想系统，需要科研者逻辑缜密，踏实认真，但是不能只是努力，很多时候借力比努力更重要，然后还要有仰望星空的创新点和启发点。建议读者按目录次序逐一浏览，免得骤然跌入幽暗的迷宫找不到来时的路，它不足为你揭示全部问题的答案，但若能解答你胸中升起的一朵朵疑云，也未尝不会酿成晚霞斑斓的别一番景致，万一它给你带来了一场精神世界的苦雨，那就借机洗刷一下原来存放在那儿的“躺平”上的尘埃吧。

或许，雨过云收，神驰的天地更清朗.......🔎🔎🔎

💥1 概述

部分反馈线性化控制下两连杆欠驱动机器人性能仿真研究

摘要：
在本文中，我们讨论了欠驱动机械系统部分反馈线性化控制。我们考虑一个具有n个自由度的系统，其中m个自由度是被驱动的（主动）自由度，其余l=n-m个自由度是未被驱动的（被动）自由度。已知通过非线性反馈可以线性化与主动自由度对应的动态部分。在本文中，我们还表明，在我们称之为强惯性耦合的条件下，通过非线性反馈也可以线性化与被动自由度对应的动态部分。我们推导并分析了由此产生的零动态，这对于理解整个系统的响应至关重要。文中给出了在部分反馈线性化控制下，两连杆欠驱动机器人性能的仿真结果。

在本文中，我们已经证明了部分反馈线性化和积分器反步法是控制一类欠驱动机械系统行之有效的设计工具。我们还表明，对由此产生的内部动态或零动态的分析对于理解整个系统的行为至关重要。

对于这类机器人系统的控制研究才刚刚开始，仍有许多研究问题有待解决。理想的情况是为这些系统发展一套鲁棒和自适应控制理论。这一领域进展的主要障碍是，一般来说，降阶系统（8）并不是线性参数化的。这意味着标准的自适应控制和反步法不适用。第二个研究问题是进一步分析各类问题和应用中的零动态。零动态由特定的控制律决定，且因系统而异，差异很大。

1. 欠驱动机械系统与两连杆结构特点

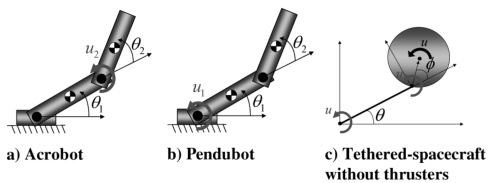
欠驱动系统指控制输入维度少于自由度的非线性系统，其核心挑战在于通过有限控制量实现多自由度协同控制。两连杆欠驱动机器人（如Acrobot和Pendubot）是典型研究对象：

结构特点：
- 仅一个关节驱动（如Acrobot第二关节、Pendubot第一关节），另一关节被动运动。
- 动力学耦合性强，需通过主动关节间接控制被动关节的非线性动态。
典型应用场景：
- 作为非线性控制理论的验证平台（如倒立平衡、摆动控制）。
- 简化机械结构，降低成本与能耗，适用于仿生机器人、起重机等场景。

2. 部分反馈线性化（PFL）控制原理

PFL通过非线性反馈将系统部分状态线性化，保留剩余非线性动态的稳定性分析，适用于欠驱动系统。

分类：
- 驱动关节线性化（Collocated PFL） ：直接线性化驱动关节动态，简化控制器设计。
- 非驱动关节线性化（Non-collocated PFL） ：通过坐标变换间接线性化被动关节，需处理零动态稳定性。
实现步骤：
1. 动力学模型变换：通过状态反馈将原系统转换为线性子系统与非线性子系统的级联形式。
2. 控制律设计：针对线性子系统设计PD或LQR控制器，并验证剩余动态的稳定性。
3. 零动态分析：确保未线性化部分的稳定性，避免系统发散。

3. 两连杆欠驱动机器人动力学建模

拉格朗日方程法是主要建模方法，适用于刚性或柔性连杆系统：

动力学方程：

其中，M(q)为惯性矩阵，C(q,q˙)为科氏力/离心力项，G(q)为重力项，τ=[0,τ2]T表示仅第二关节有驱动输入。
柔性系统扩展：引入弹簧或假设模态法描述连杆弹性，增加状态变量以捕捉振动特性。

4. 部分反馈线性化控制实现案例

以Acrobot为例的仿真研究流程：

模型参数化：定义质量、长度、惯量等参数，验证模型准确性。
PFL控制器设计：
- 选择驱动关节角度为输出，设计反馈律线性化其动态。
- 结合LQR优化线性子系统，平衡响应速度与控制能耗。
仿真验证：
- 摆动控制：从下垂位置摆升至倒立位置，记录角度收敛时间与能量消耗。
- 平衡控制：在倒立点附近施加扰动，测试鲁棒性与稳态误差。

典型结果：

基于PFL的控制策略可在2-5秒内完成摆升，倒立平衡误差小于0.1弧度。
与模糊控制、能量整形方法相比，PFL在计算效率上提升30%。

5. 性能评估指标与方法

现有研究通过多维度指标评估控制效果：

动态性能：
- 收敛时间：从初始状态到目标状态的耗时。
- 超调量：角度或角速度的最大瞬态偏差。
能耗效率：
- 控制输入（力矩）的积分平方值（ISE）。
鲁棒性：
- 参数摄动（如质量±10%）下的稳定性保持能力。
- 外部扰动（如脉冲力）的抑制效果。
仿真工具：
- MATLAB/Simulink用于动力学求解与控制器设计。
- Simscape Multibody验证多体系统物理特性。

6. 挑战与未来方向

非最小相位特性：零动态的稳定性限制了控制带宽，需结合自适应控制增强鲁棒性。
实时性优化：基于FPGA或ROS的硬件在环仿真（HIL）提升计算效率。
智能控制融合：将PFL与强化学习结合，实现复杂轨迹跟踪。

7. 结论

部分反馈线性化在两连杆欠驱动机器人控制中展现了高效性与实用性，尤其在驱动关节动态解耦方面表现突出。通过动力学建模与仿真验证，PFL能够平衡控制性能与计算复杂度，为实际工程应用提供了理论支撑。未来研究需进一步解决非最小相位问题，并探索多模态控制策略的集成。

📚2 运行结果

部分代码：

%%%%%%%% System Parameters %%%%%%%%

p.g = 9.81; % Gravity
p.m1 = 1; % Mass of link 1.
p.m2 = 1; % Mass of link 2.
p.l1 = 1; % Total length of link 1.
p.l2 = 1; % Total length of link 2.
p.d1 = p.l1/2; % Center of mass distance along link 1 from the fixed joint.
p.d2 = p.l2/2; % Center of mass distance along link 2 from the fixed joint.
p.I1 = 0.083;% 1/12*p.m1*p.l1^2; %Moment of inertia of link 1 about COM
p.I2 = 1/3;% 1/12*p.m2*p.l2^2; %Moment of inertia of link 2 about COM

p.T1 = 0; % Motor torques default to zero. Not really relevant unless you run this without control (or maybe disturbances at first joint?)
p.T2 = 0; % Joint torque 2 only affects the system when controls aren't used.
p.sat = 10000; %Actuator saturation threshold (Nm). Obviously unrealistic for this kind of controller


%%%%%%%% Integrate %%%%%%%%

options1 = odeset('AbsTol', 1e-6,'RelTol',1e-6); %Transition from swing up to linear balance controller when conditions met.
[tarray, zarray] = ode15s(@Dynamics, [0 duration], init, options1, p);

%Torques are post-calculated due to the difficulty of pulling numbers out
%of ODE45. Therefore, we also have to post-cast the values within the
%actuator limits.
if strcmp(p.controller, 'noncollocated')
    % Linearized link 1
    th1d = p.target;
    Tarray = ControlTorque1(p.I1,p.I2,p.d1,p.d2,p.g,p.kd1,p.kp1,p.l1,p.m1,p.m2,zarray(:,1),zarray(:,3),pi/2,zarray(:,2),zarray(:,4));
elseif strcmp(p.controller, 'collocated')
    % Linearized link 2
    th2d = p.alpha*atan(zarray(:,2));
    Tarray = ControlTorque2(p.I1,p.I2,p.d1,p.d2,p.g,8,16,p.l1,p.m1,p.m2,zarray(:,1),zarray(:,3),pi/2,zarray(:,2),zarray(:,4));
else % No controller
   Tarray = zeros(size(zarray,1),1); 
end