六自由度高超声速飞行器的建模与控制器设计

目录

1.六自由度高超声速飞行器建模引言

2.六自由度高超声速飞行器概述

3.Simulink仿真建模

4.仿真结果

---

1.六自由度高超声速飞行器建模引言

       六自由度高超声速飞行器是一种复杂的飞行器，它在六个自由度（三个平移自由度和三个旋转自由度）上具有运动能力。建模和控制这种飞行器需要综合考虑气动、动力学和控制理论等多个方面的知识。以下是建模和控制六自由度高超声速飞行器的一般步骤：

1. 飞行器建模：

• 动力学模型：建立飞行器的动力学模型，包括质心运动和旋转运动的方程。这涉及到力、力矩、质心位置和方向的关系。
• 气动模型：考虑飞行器在高超声速条件下的气动特性，如升力、阻力和控制面效应等。这通常需要使用计算流体力学（CFD）或实验数据来估算。
• 控制面模型：建立飞行器控制系统的模型，包括控制面的动力学和效应。这有助于控制系统的设计。
• 传感器模型：考虑用于测量姿态和位置的传感器，如陀螺仪、加速度计和GPS等。建立传感器的模型以估计状态信息。

2. 控制器设计：

• 状态反馈控制器：设计一个状态反馈控制器，以根据飞行器的当前状态来生成控制指令。这通常涉及到解决线性或非线性控制问题，具体取决于系统动力学。
• 轨迹跟踪控制：如果需要，设计轨迹跟踪控制器，以使飞行器沿着预定轨迹飞行。
• 鲁棒性和鲁棒控制：考虑飞行器面临的不确定性和扰动，设计鲁棒控制器，以保持控制性能在不确定性下的稳定性。
• 非线性控制：如果飞行器动力学是非线性的，则可能需要采用非线性控制方法，如反馈线性化、模型预测控制（MPC）或滑模控制。

3. 仿真和验证：

• 使用建立的模型进行仿真，验证控制器的性能和稳定性。在不同飞行条件下进行仿真测试，包括失控情况的模拟。
• 调整控制器参数以满足性能要求，包括姿态和位置控制。

2.六自由度高超声速飞行器概述

       高超声速飞行器是指飞行马赫数大于5的飞行器，它是一种近空间飞行器。“近空间”可简单理解为：现有飞机飞行的最高高度（约20Km）和卫星运行轨道的最低高度（约100Km）间的空域。近空间飞行器可定性描述为：能持久稳定运行于近空间执行特定任务的各种飞行器。近空间飞行器的发展涉及国家安全与和平利用空间，是目前国际竞相争夺空间技术的焦点之一，是综合国力的体现。近空间飞行器的出现将促生新的作战样式，改写联合作战理论，并对未来技术局部战争产生重大影响。

       高超声速飞行器与常规的飞行器相比其整体布局采用机身发动机一体化设计，这使得各个子系统之间具有更强的耦合性和非线性。为了满足高超声速飞行器在复杂的飞行条件下仍然拥有稳定的飞行性能和良好的飞行品质，必须采用全新的控制手段。

      高超声速飞行器各力作用于刚体中心如图所示：

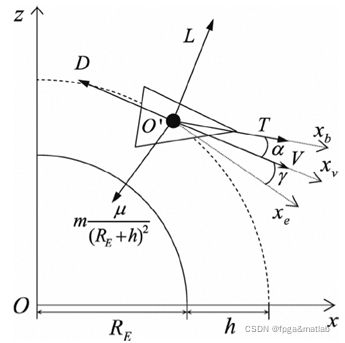
高声速飞行器纵向动力学模型的非线性方程组可以按照其受力情况在速度坐标系上描述为:

3.Simulink仿真建模

建立如下的仿真模型：

 

4.仿真结果

输出的四个变量V，alpha，theta，q，其仿真结果如下所示：

对于速度：

对于高度：

Clear

clc

%**********建立系统模型**********%

A=[-1.4225e-13 -9.9688 -16.641 0 -5.2784e-22;

   9.7346e-7 0 0.086872 0 5.8625e-10; 

   -9.7346e-7 0 -0.086872 1 -5.8625e-10;

   -1.6167e-15 0 0.78031 -0.076265 0;

   -1.6645e-16 4525.6 0 0 0];

B=[16.219 0 ;6.1181e-5 0 ;-6.1181e-5 0 ;0 3.6619;0 0];

C=[1 0 0 0 0 ; 0 0 0 0 1];

D=0;

%**********判断系统能控能观测性**********%

Tc=ctrb(A,B);

To=obsv(A,C);

rank(Tc)

rank(To)

%**********极点配置设计**********%

p1=[-8,-7,-1+0.8i,-1-0.8i,-6]

K1=place(A,B,p1) 

A1=A-B*K1  % 极点配置后状态反馈阵K3

figure(1)

sys1=ss(A1,B,C,D);

step(sys1)

grid on

%**********LQR控制设计**********%

Q21=[100 0 0 0 0;0 1 0 0 0;0 0 1 0 0;0 0 0 1 0;0 0 0 0 1]

Q22=[100 0 0 0 0;0 1 0 0 0;0 0 1 0 0;0 0 0 1 0;0 0 0 0 2.25]

Q23=[100 0 0 0 0;0 1 0 0 0;0 0 1 0 0;0 0 0 1 0;0 0 0 0 5]

R2=[100 0;0 1]

%求解Rcaati方程解出P并计算出最优反馈阵K，相应的r为LQR设计后系统的极点，K为LQR控制器状态反馈阵

[K21,P21,r21]=lqr(A,B,Q21,R2)

[K22,P22,r22]=lqr(A,B,Q22,R2)

[K23,P23,r23]=lqr(A,B,Q23,R2)

%**********H无穷控制器设计**********%

B1=[-0.036524 0.96679;0 0; 3.9195e-5 0.081626;-0.0020147 -3.0354; 0 0];

% 干扰模型阵

C1=[1 0 0 0 0;0 1 0 0 0;0 0 1 0 0;0 0 0 1 0;0 0 0 0 1;0 0 0 0 0;0 0 0 0 0];

r=3.3;             

R3=B*B'-(1/r^2)*B1*B1';

Q3=C1'*C1

[p31,p32,lamp,perr,wellposed,P3] =aresolv(A,Q3,R3)

K3=B'*P3;  % H无穷控制器反馈阵K3

%**********BODE图**********%

A1=A-B*K1  % 极点配置后系统A阵

A2=A-B*K22 % K22为LQR控制器的状态反馈阵K

A3=A-B*K3  % H无穷设计后系统A阵

sys=ss(A,B,C,D)   % 原系统

sys2=ss(A2,B,C,D) % LQR设计后系统

sys3=ss(A3,B1,C,D)% H无穷设计后系统

figure(2)

bode(sys,'--')    % 原系统伯德图

hold on

bode(sys2,'.')    %LQR设计后系统伯德图

hold on

bode(sys3,'r')    %H无穷设计后原系统伯德图

grid on

A08-07