PS: 本篇文章为台大机器人学学习笔记,B站视频链接如下:
https://www.bilibili.com/video/BV1v4411H7ez?p=7
1. 刚体(rigid body)状态描述:
(DOF:degree of freedom,自由度)
(1)在大地坐标系({W}, world frame)下:
| 平面 | 空间 | |
|---|---|---|
| 移动(DOF) | 2 | 3 |
| 转动(DOF) | 1 | 3 |
–> 在空间中,用6个参数表示刚体运动状态。
(2) 如何整合表示刚体状态:
进一步,在刚体的定点(多为质心)上建立坐标系({B},body frame):
| 移动 | 转动 |
|---|---|
| 由{B}的原点位置判定 | 由{B}的姿态判定 |
(3) 刚体的连动状态如何描述:
利用各个(6个)DOF的微分,将位移(displacement)和姿态(orientation)**转换到速度(velocity)和加速度(acceleration)**等连动状态:

2. 刚体移动描述:
(1)移动:
用向量P
P
⃗
=
[
P
x
P
y
P
z
]
\vec P = \left[ \begin{array}{l} {P_x}\\ {P_y}\\ {P_z} \end{array} \right]
P=⎣⎡PxPyPz⎦⎤描述原点的状态变化:

(2)向量可表达空间关系的两个方式:
① 表示body frame的原点

② 表示body frame 的方向
3. 刚体转动描述:
描述{B}相对{A}的姿态: rotation matrix
(由于对于机械臂来说关节多,因此这里先用A来表示固定的坐标系,而不用W)

公式描述:

左上角为基准:B在A坐标系下的描述;
R
R
R的三个分量为由{A}看{B}的三个basis:
X
^
B
,
Y
^
B
,
Z
^
B
\hat{X}_B,\hat{Y}_B,\hat{Z}_B
X^B,Y^B,Z^B
投影的角度:将 X ^ B , Y ^ B , Z ^ B \hat{X}_B,\hat{Y}_B,\hat{Z}_B X^B,Y^B,Z^B分别分解到 A A A坐标系下;
4 R的特性
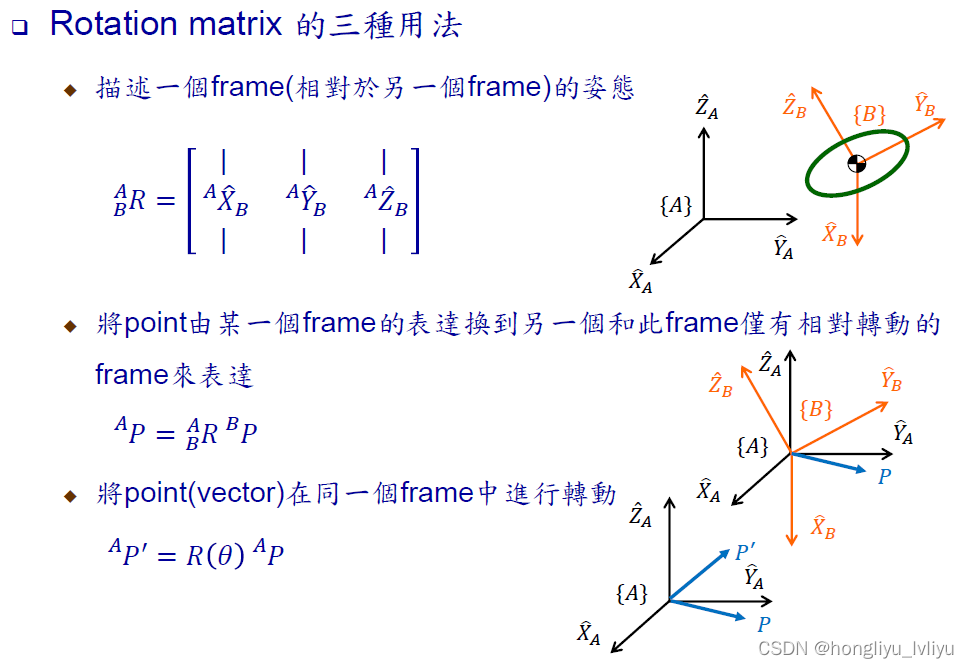
4.1 R描述一个frame的姿态
(1)特性
①
X
^
B
⋅
Y
^
A
\hat{X}_{B} \cdot \hat{Y}_{A}
X^B⋅Y^A为内积,内积前后互换无影响,结果为数字,因此可以对所有内积做前后互换,得到:

即:
B
A
R
=
A
B
R
T
{}_{B}^{A}R={}_{A}^{B}{{R}^{T}}
BAR=ABRT
②

即:
B
A
R
=
A
B
R
T
=
A
B
R
−
1
_{B}^{A}R=_{A}^{B}{{R}^{T}}=_{A}^{B}{{R}^{-1}}
BAR=ABRT=ABR−1
(2)特性总结
- 符合正交矩阵(orthogonal matrix)Q特性:
Q Q T = Q T Q = I , Q − 1 = Q T QQ^{T}=Q^{T}Q=I,Q^{-1}=Q^{T} QQT=QTQ=I,Q−1=QT - 矩阵中的列向量:长度为1;两两互相垂直。
- R R R包含9个数字,但上述内容包含6个条件,即 R R R中只包含了三个自由度,对应了空间中转动只具有3DOFs
4.2 R描述转换关系

向量
P
P
P:
B
P
=
B
P
x
X
^
B
+
B
P
y
Y
^
B
+
B
P
z
Z
^
B
,
^{B}P=^{B}P_{x} \hat{X}_{B}+^{B}P_{y} \hat{Y}_{B}+^{B}P_{z} \hat{Z}_{B},
BP=BPxX^B+BPyY^B+BPzZ^B,
A
P
=
A
P
x
X
^
A
+
A
P
y
Y
^
A
+
A
P
z
Z
^
A
^{A}P=^{A}P_{x} \hat{X}_{A}+^{A}P_{y} \hat{Y}_{A}+^{A}P_{z} \hat{Z}_{A}
AP=APxX^A+APyY^A+APzZ^A
其中,
A
P
x
,
A
P
y
^{A}P_{x},^{A}P_{y}
APx,APy等表示在对应方向上的长度。
进一步,可以将
A
P
x
^{A}P_{x}
APx展开为:(
B
P
^{B}P
BP带入上式)
A
P
x
=
B
P
⋅
X
^
A
=
X
^
B
⋅
X
^
A
B
P
x
+
Y
^
B
⋅
X
^
A
B
P
y
+
Z
^
B
⋅
X
^
A
B
P
z
^{A}P_{x}= ^{B}P \cdot \hat{X}_{A} =\hat{X}_{B} \cdot \hat{X}_{A} {}^{B}P_{x}+\hat{Y}_{B} \cdot \hat{X}_{A} {}^{B}P_{y}+\hat{Z}_{B} \cdot \hat{X}_{A} {}^{B}P_{z}
APx=BP⋅X^A=X^B⋅X^ABPx+Y^B⋅X^ABPy+Z^B⋅X^ABPz
同理可得
A
P
y
,
A
P
z
^{A}P_{y},^{A}P_{z}
APy,APz,

进一步有:

即有:
A
P
=
B
A
R
B
P
,
{}^{A}P={}^{A}_{B}R {}^{B}P,
AP=BARBP,
B
P
{}^{B}P
BP为
P
P
P在{B}下的表达。
- 功能:使用 R R R, 将某坐标点从某个frame转到另一个frame。
4.3 R描述物体转动状态

以
B
A
R
{}^{A}_{B}R
BAR等于
X
^
B
,
Y
^
B
,
Z
^
B
\hat{X}_{B},\hat{Y}_{B},\hat{Z}_{B}
X^B,Y^B,Z^B三个向量在
A
{A}
A的投影得到的列向量拼接为基础,可以得到以
Z
^
A
\hat{Z}_{A}
Z^A为旋转轴,
θ
\theta
θ为旋转角度的表示(角度由于常用所以进一步进行简写):

绕
X
^
A
\hat{X}_{A}
X^A有:
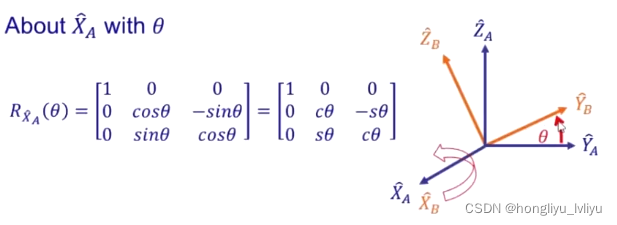
绕
Y
^
A
\hat{Y}_{A}
Y^A有:

4.4 R的功能总结
























 323
323

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








