(本文数据来自https://wenku.baidu.com/view/03d586024afe04a1b171de8d.html)
(2018年11月21日更新)
D-H)建模方法是由Denavit和Hartenberg 提出的一种建模方法,主要用在机器人运动学上,这种方法在每个连杆上建立一个坐标系,通过齐次坐标变换来实现两个连杆上坐标的变换,在多连杆串联的系统中,多次使用齐次坐标变换,就可以建立首末坐标系的关系。学习DH建模的主要知识点如下:
1、会齐次坐标变换(这是机器人运动学的基础知识)
2、知道DH建模中α,a,d,θ这四个量对应于连杆上的那些地方。
3、对于已知的连杆机构,会列些DH参数表。
4、会列些最终坐标变换的等式,建立机械臂末端与基座的坐标关系。
DH建模分原版和修正版,修正版克服了原版建模中的一些问题,比较常用,本文介绍修正版DH建模方法
预备知识:
1、齐次坐标系
齐次坐标系的定义可以参阅百度百科,核心就是n维向量的n+1维表示方法,比如,平面的一个点:(2,3),齐次坐标表示为(2w,3w,w),w为非零实数,同理,对于空间中某点的坐标(x,y,z),齐次坐标可表示为(xw,yw,zw,w),若令w取1,就是(x,y,z,1),这就是三维坐标的齐次坐标表示方法(不唯一)。
齐次坐标表示在计算机图学和机器人学中有着广泛的应用,优点说出来都很难懂,但在机器人学领域,主要优点就是将旋转变换和平移变换统一成了4×4的矩阵运算,任何一种复合变换(旋转与平移可以同时存在),都可以表示成一个4×4的齐次变换矩阵。
2、齐次坐标变换矩阵
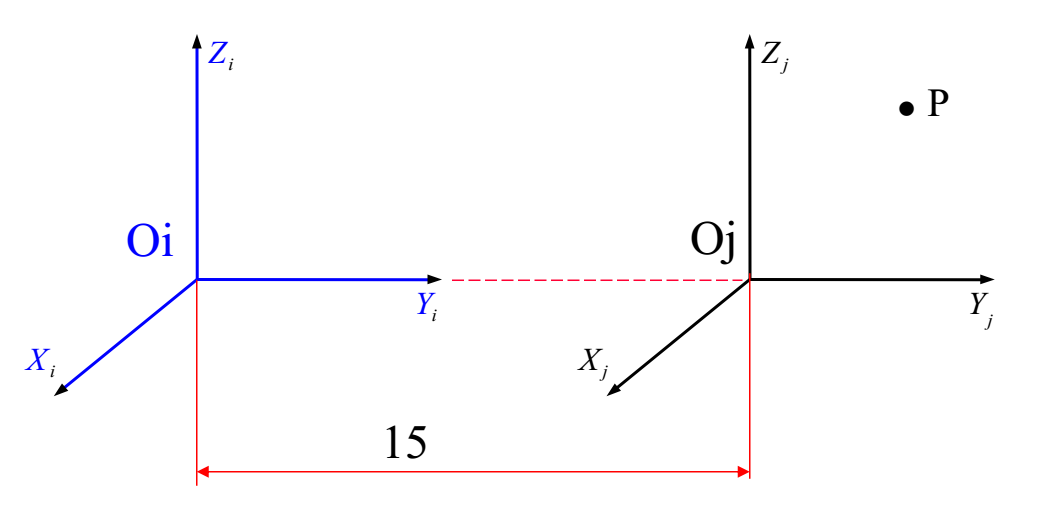
若不使用齐次坐标表示法,对于三维空间下的平移,可以在原有坐标的基础上加一个向量这么表示:Pi=Pj+Pij,下图中,若P点在j坐标系坐标为(1,1,1),i到j的平移向量为(0,15,0),则P点在i坐标系下的表示为(1,16,1),应该很好理解吧。
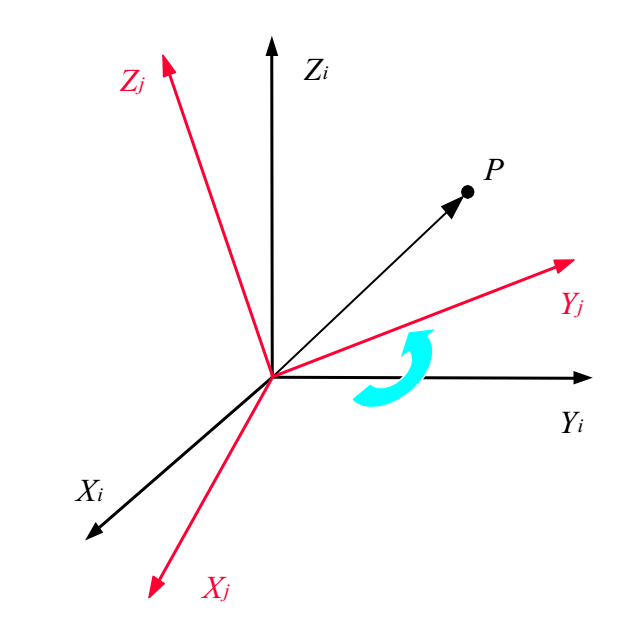
若要表示旋转,稍微复杂点,由i系转到j系,要考虑到轴与轴之间的多个夹角,最终得到一个旋转姿态矩阵R,表达式里看着有好多夹角余弦,其实若只绕着某个轴转,很多值都会变得简洁。
上面说的是不使用齐次坐标的情况,若使用齐次坐标,就是将旋转与平移组合在一起,构建一个4*4的齐次变换矩阵,齐次变换矩阵长相如下所示:
仔细看一下,就是将上面说的R和P组合在了一起,右下角填了一个1,其余地方补0,这就是齐次变换矩阵。当看到一个44的齐次变换矩阵时,你一眼就能知道左上角的33表示旋转,右边一列表示平移,下面一行是固定写法,以后再说变换时,就不再把旋转与平移割裂开了,这一个矩阵就表示综合的变换。
上面是预备知识,下面才是D-H建模正题。
现在的机械臂很多都是旋转关节与滑动环节的链式组合,假设你知道机械臂各个连杆的尺寸,但各个关节都在动,你如何确定末端的位置?DH建模要解决的根本问题就是建立机械臂末端与基座位姿位姿关系的问题。
首先,需要知道DH建模里的一些基本概念,若对下述概念模棱两可的话,后续建模









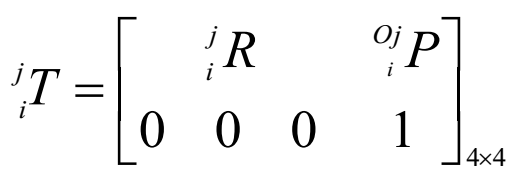
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








