图优化算法（1）_利用高斯牛顿的方法作位姿图优化

最新推荐文章于 2024-04-04 14:25:46 发布

什么都会一点儿的自动驾驶工程狮

最新推荐文章于 2024-04-04 14:25:46 发布

阅读量721

点赞数 3

分类专栏： 2D SLAM 优化算法基础文章标签：图优化 ROS 激光SLAM C++ 高斯牛顿

本文链接：https://blog.csdn.net/lzy6041/article/details/90317989

版权

2D SLAM 同时被 2 个专栏收录

7 篇文章 0 订阅

订阅专栏

优化算法基础

2 篇文章 0 订阅

订阅专栏

本节是对激光SLAM课程中图优化课程理论学习后的代码实现及对应理论说明。

1.要完成的工作

1）需要实现Jacobian矩阵和误差项的计算。
2）需要构建线性系统。

2.要达到的目标

利用高斯牛顿方法进行全局优化。

3.测试结果

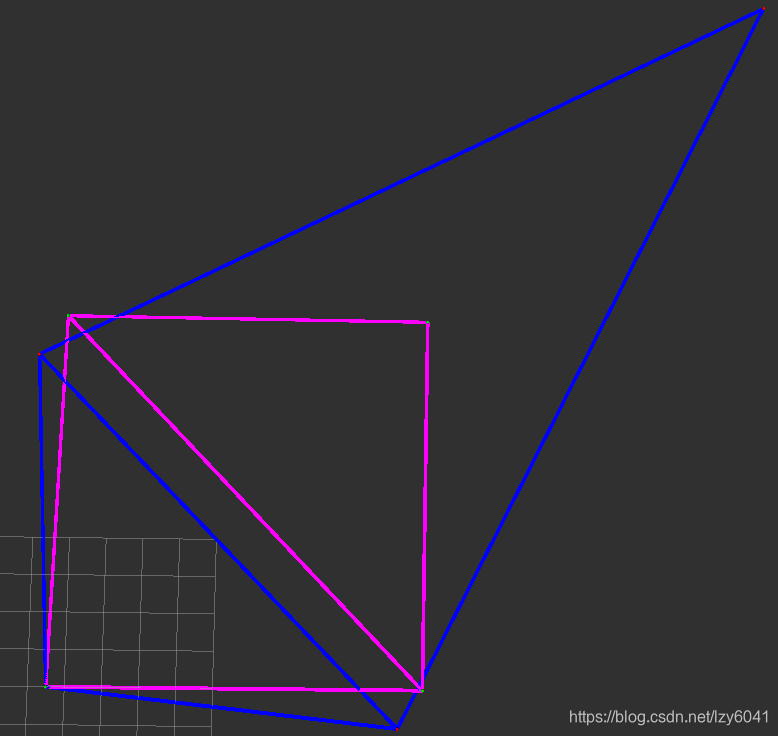
在这里插入图片描述
上图是对test_quadrat数据集合的测试结果。蓝色为优化前的位姿轨迹，粉色为优化后的位姿轨迹。

4.关键函数及对应理论分析

4.1 主函数

主函数主要分为四个部分：
1）.从本地读取节点及边的数据，保存到Vertexs、Edges向量中，并在rviz显示。

std::vector<Eigen::Vector3d> Vertexs;//定义一个3*1的向量，存放节点数据
std::vector<Edge> Edges;//定义一个向量，存放边的数据xi,xj,测量值，信息矩阵

ReadVertexInformation(VertexPath,Vertexs);//读取节点信息，存放在Vertexs向量中
ReadEdgesInformation(EdgePath,Edges);//读取边的信息，存放在Edges向量中

PublishGraphForVisulization(&beforeGraphPub,Vertexs,Edges);

关于数据的说明：
节点数据：

VERTEX2 0 0.5 1 0
VERTEX2 1 10 0 1.570796
VERTEX2 2 20 20 3.14159
VERTEX2 3 0 10 -1.570796

说明：
关于节点的数据结构：

std::vector<Eigen::Vector3d>& nodes

将以上数据从result[]传递给nodes。

int id = stringToNum<int>(results[1]);
double x = stringToNum<double>(results[2]);
double y = stringToNum<double>(results[3]);
double theta = stringToNum<double>(results[4]);
Eigen::Vector3d pose(x,y,theta);
nodes.push_back(pose);

边数据：

EDGE2 0 1 10.2 0 0 500.000000 0.000000 500.000000 5000.000000 0.000000 0.000000
EDGE2 1 2 10 0 0 500.000000 0.000000 500.000000 5000.000000 0.000000 0.000000
EDGE2 2 3 9.9 0 0 500.000000 0.000000 500.000000 5000.000000 0.000000 0.000000
EDGE2 3 0 10.1 0 0 500.000000 0.000000 500.000000 5000.000000 0.000000 0.000000
EDGE2 3 1 9.8 10.1 3.1415 500.000000 0.000000 500.000000 5000.000000 0.000000 0.000000

说明：
关于边的数据结构定义：

typedef struct edge
{
  int xi,xj;
  Eigen::Vector3d measurement;
  Eigen::Matrix3d infoMatrix;
}Edge;
std::vector<Edge>& edges

将以上数据从result[]传递给Edge。

int xi = stringToNum<int>(results[1]);
int xj = stringToNum<int>(results[2]);

double dx = stringToNum<double>(results[3]);
double dy = stringToNum<double>(results[4]);
double dtheta = stringToNum<double>(results[5]);

double inf_xx  = stringToNum<double>(results[6]);
double inf_xy  = stringToNum<double>(results[7]);
double inf_yy  = stringToNum<double>(results[8]);
double inf_tt  = stringToNum<double>(results[9]);
double inf_xt  = stringToNum<double>(results[10]);
double inf_yt  = stringToNum<double>(results[11]);
Edge tmpEdge;
tmpEdge.xi = xi;
tmpEdge.xj = xj;
tmpEdge.measurement = Eigen::Vector3d(dx,dy,dtheta);
tmpEdge.infoMatrix << inf_xx,inf_xy,inf_xt,
                      inf_xy,inf_yy,inf_yt,
                      inf_xt,inf_yt,inf_tt;
edges.push_back(tmpEdge)

2）.计算整个pose-graph的误差（优化前的误差）

double initError = ComputeError(Vertexs,Edges);

对误差函数的理解
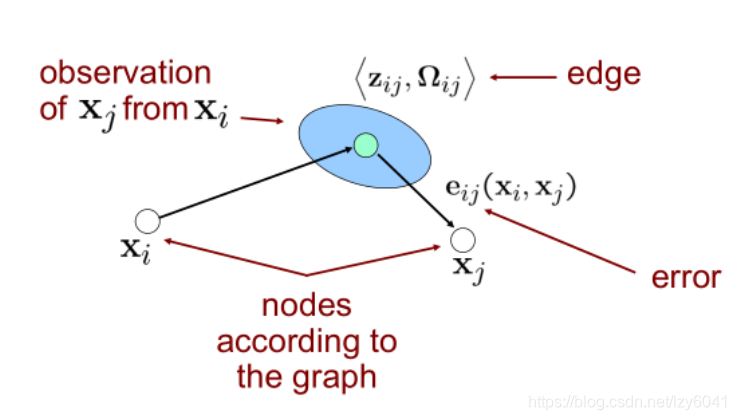
在这里插入图片描述
$x_i$ ， $x_j$ 是由里程计得到两点在世界坐标系下的坐标，对应到世界坐标系的转换矩阵就可以得到是 $X_i$ ， $X_j$ ，由雷达观测得到 $j$ 时刻，在 $x_i$ 的坐标系下的位置是三维向量 $z_{ij}$ ，可以得到转换矩阵 $Z_{ij}$ 。
两者转换代码如下：

//位姿-->转换矩阵
Eigen::Matrix3d PoseToTrans(Eigen::Vector3d x)
{
    Eigen::Matrix3d trans;
    trans << cos(x(2)),-sin(x(2)),x(0),
             sin(x(2)), cos(x(2)),x(1),
                     0,         0,    1;

    return trans;
}


//转换矩阵－－＞位姿
Eigen::Vector3d TransToPose(Eigen::Matrix3d trans)
{
    Eigen::Vector3d pose;
    pose(0) = trans(0,2);
    pose(1) = trans(1,2);
    pose(2) = atan2(trans(1,0),trans(0,0));

    return pose;
}

误差定义就是里程计得到的位置，在雷达观测值位置坐标系下的位置。先求 $E_{ij}$ ，再转换为三维向量 $e_{ij}$ ，设在 $x_j$ 坐标系下一点 $m$ ，点 $m$ 在世界坐标系下的位置就是 $X_j×m$ ，也可以写成 $X_i×Z_{ij}×E_{ij}×m$ 。

即有 $X_i×Z_{ij}×E_{ij}=X_j$ ，
所以 $Eij = Z_{ij}.inv * X_i.inv * Xj$ ，再转换为向量形式。
$X_i.inv * X_j$ 的向量表示 $x_j$ 原点在 $x_i$ 坐标系下坐标。

double ComputeError(std::vector<Eigen::Vector3d>& Vertexs,
                    std::vector<Edge>& Edges)
{
    double sumError = 0;
    for(int i = 0; i < Edges.size();i++)
    {
        Edge tmpEdge = Edges[i];
        Eigen::Vector3d xi = Vertexs[tmpEdge.xi];
        Eigen::Vector3d xj = Vertexs[tmpEdge.xj];
        Eigen::Vector3d z = tmpEdge.measurement;
        Eigen::Matrix3d infoMatrix = tmpEdge.infoMatrix;

        Eigen::Matrix3d Xi = PoseToTrans(xi);
        Eigen::Matrix3d Xj = PoseToTrans(xj);
        Eigen::Matrix3d Z  = PoseToTrans(z);

        Eigen::Matrix3d Ei = Z.inverse() *  Xi.inverse() * Xj;

        Eigen::Vector3d ei = TransToPose(Ei);


        sumError += ei.transpose() * infoMatrix * ei;
    }
    return sumError;
}

3）.线性化与求解

Eigen::VectorXd dx = LinearizeAndSolve(Vertexs,Edges);

雅克比矩阵推导，
$e_{ij}$ 由 $E_{ij}$ 推导而来的向量形式， $X_i.inv * X_j$ 的向量表示 $x_j$ 原点在 $x_i$ 坐标系下坐标，然后对 $x_i，x_j$ 的 $(x, y, t h e t a)$ 求导，得到雅克比矩阵。
在这里插入图片描述

/**
 * @brief CalcJacobianAndError
 *         计算jacobian矩阵和error
 * @param xi    fromIdx
 * @param xj    toIdx
 * @param z     观测值:xj相对于xi的坐标
 * @param ei    计算的误差
 * @param Ai    相对于xi的Jacobian矩阵
 * @param Bi    相对于xj的Jacobian矩阵
 */
void CalcJacobianAndError(Eigen::Vector3d xi,Eigen::Vector3d xj,Eigen::Vector3d z,
                          Eigen::Vector3d& ei,Eigen::Matrix3d& Ai,Eigen::Matrix3d& Bi)
{
    //TODO--Start
    Eigen::Matrix3d Xi = PoseToTrans(xi);
    Eigen::Matrix3d Xj = PoseToTrans(xj);
    Eigen::Matrix3d Z  = PoseToTrans(z);

    Eigen::Matrix3d Ei = Z.inverse() *  Xi.inverse() * Xj;

    //误差 ei
     ei = TransToPose(Ei);

    Eigen::Matrix2d Rxi = Xi.block(0,0,2,2);
    Eigen::Matrix2d Rij = Z.block(0,0,2,2);

    Eigen::Vector2d ti,tj;
    ti << xi(0),xi(1);
    tj << xj(0),xj(1);

    double theta = xi(2);

    Eigen::Matrix2d dRxi;
    dRxi << -sin(theta),cos(theta),
            -cos(theta),-sin(theta);

    //jacobian
    Ai.setZero();
 //matrix.block(i,j,p,q);表示返回从矩阵的(i, j)开始，每行取p个元素，每列取q个元素所组成的临时新矩阵对象，原矩阵的元素不变。
    Ai.block(0,0,2,2) = - Rij.transpose() * Rxi.transpose();
    Ai.block(0,2,2,1) = Rij.transpose() * dRxi * (tj - ti);
    Ai(2,2) = -1;


    Bi.setZero();
    Bi.block(0,0,2,2) = Rij.transpose() * Rxi.transpose();
    Bi(2,2) = 1;

    //TODO--end
}

非线性最小二乘优化
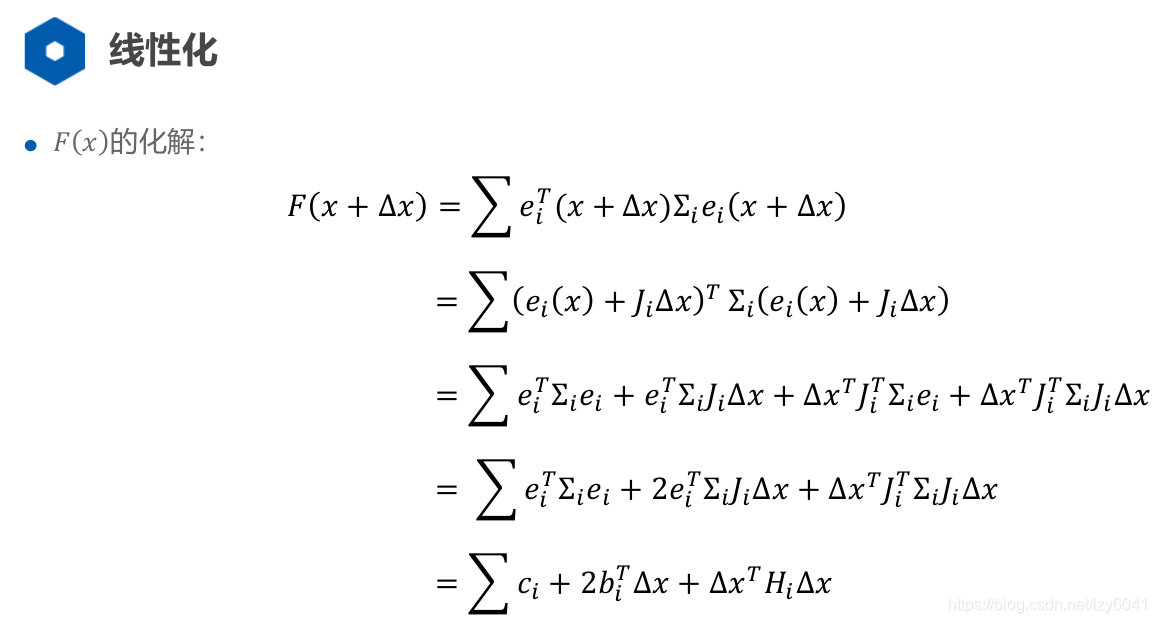
在这里插入图片描述
循环每一条边（约束），求出该边的误差项 $e_i$ 和雅克比矩阵，按上图构造出 $b$ 和 $H$ ，叠加。
函数体如下：


/**
 * @brief LinearizeAndSolve
 *        高斯牛顿方法的一次迭代．
 * @param Vertexs   图中的所有节点
 * @param Edges     图中的所有边
 * @return          位姿的增量
 */
Eigen::VectorXd  LinearizeAndSolve(std::vector<Eigen::Vector3d>& Vertexs,std::vector<Edge>& Edges)
{
    //申请内存
    Eigen::MatrixXd H(Vertexs.size() * 3,Vertexs.size() * 3);
    Eigen::VectorXd b(Vertexs.size() * 3);
    H.setZero();
    b.setZero();
    //固定第一帧
    Eigen::Matrix3d I;
    I.setIdentity();
    H.block(0,0,3,3) += I;
    //构造H矩阵　＆ b向量
    for(int i = 0; i < Edges.size();i++)
    {
        //提取信息
        Edge tmpEdge = Edges[i];
        Eigen::Vector3d xi = Vertexs[tmpEdge.xi];
        Eigen::Vector3d xj = Vertexs[tmpEdge.xj];
        Eigen::Vector3d z = tmpEdge.measurement;
        Eigen::Matrix3d infoMatrix = tmpEdge.infoMatrix;

        //计算误差和对应的Jacobian
        Eigen::Vector3d ei;
        Eigen::Matrix3d Ai;
        Eigen::Matrix3d Bi;
        CalcJacobianAndError(xi,xj,z,ei,Ai,Bi);

        Eigen::Matrix3d Hii,Hij,Hji,Hjj;
        Hii = Ai.transpose() * infoMatrix * Ai;
        Hij = Ai.transpose() * infoMatrix * Bi;
        Hji = Bi.transpose() * infoMatrix * Ai;
        Hjj = Bi.transpose() * infoMatrix * Bi;

        int idx = tmpEdge.xi;
        int jdx = tmpEdge.xj;

        H.block(3*idx,3*idx,3,3) += Hii;
        H.block(3*idx,3*jdx,3,3) += Hij;
        H.block(3*jdx,3*idx,3,3) += Hji;
        H.block(3*jdx,3*jdx,3,3) += Hjj;

        Eigen::Vector3d bi,bj;
        bi = (ei.transpose() * infoMatrix * Ai).transpose();
        bj = (ei.transpose() * infoMatrix * Bi).transpose();

        b(3*idx) += bi(0);
        b(3*idx+1) += bi(1);
        b(3*idx+2) += bi(2);

        b(3*jdx) += bj(0);
        b(3*jdx+1) += bj(1);
        b(3*jdx+2) += bj(2);

    }

什么都会一点儿的自动驾驶工程狮

关注

3
点赞
踩
9

收藏

觉得还不错? 一键收藏
0
评论
图优化算法（1）_利用高斯牛顿的方法作位姿图优化

该节主要是通过前期对理论的学习，利用高斯牛顿的方法进行POSE_GRAPH的优化。1）需要实现Jacobian矩阵和误差项的计算。2）需要构建线性系统。首先我们看主函数main.cpp#include <gaussian_newton.h>#include <readfile.h>#include <ros/ros.h>#include <...
复制链接

扫一扫