stanley 轨迹跟踪算法

”悟道“

已于 2023-01-06 09:27:33 修改

阅读量3.1k

点赞数 5

分类专栏：控制文章标签：人工智能

于 2022-12-29 17:02:13 首次发布

本文链接：https://blog.csdn.net/m0_48707860/article/details/128484886

版权

控制专栏收录该内容

5 篇文章 0 订阅

订阅专栏

一：简单了解

简介：Stanley是一种轨迹跟踪算法；

Stanley control low：

$\delta (t) = \theta _{e}(t) + tan^{-1}(\frac{ke(t)}{v_{f}t}), \delta (t)\in [\delta _{min},\delta _{max}]$

ComputerControlcmd函数，根据Stanley算法的公式进行代码的编写，所以需要调用接下来的误差计算函数，然后整个前轮转角控制命令分为两部分，分别是由航向误差和由横向误差引起的转角。需要注意的是：

1.计算反正切函数值时，建议使用atan2函数，其返回值为点和原点连线与x轴正方向的夹角，值域对应为-pi到+pi;

2.实际的前轮转角有一个范围，即 $\delta (t)\in [\delta _{min},\delta _{max}]$ ,所以需要对其进行限幅处理。

///**to-do**/计算需要的控制命令
//实际对应的stanley模型，并将获得的控制命令传递给汽车
//提示，在该函数中你需要调用计算误差
void StanleyController::ComputeControlCmd(
    const VehicleState &vehicle_state,
    const TrajectoryData &planning_published_trajectory.ControlCmd &cmd){
//控制的轨迹
trajectory_points_ = planning_published_trajectory.trajectory_points;
double e_y = 0.0;
double e_theta = 0.0;

cout << "vehicle_state.heading: " << vehicle_state.heading << endl;
ComputeLateralErrors(vehicle_state.x, vehicle_state.y, vehicle_state.heading,
                e_y,e_theta);

cout << "e_theta: " << e_theta << endl;
cout << "e_y: " << e_y <<endl;
double steer_angel = 
    (e_theta + std::atan2(k_y_ * e_y, vehicle_state.velocity));

//控制对应的转角
if(steer_angle > M_PI / 12){
    steer_angle = M_PI / 12;
}else if(steer_angle < -M_PI / 12){
    steer_angle = -M_PI / 12;
}

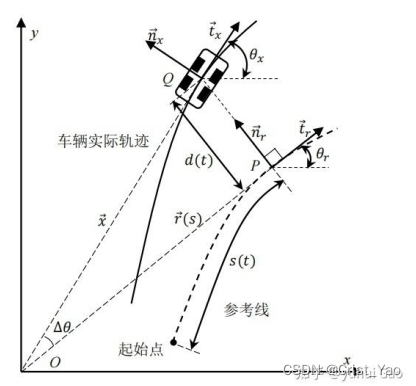
上图展示的是车辆的实际行驶轨迹和参考线之间相关关系；

ComputeLateralErrors函数，也就是分别表示航向误差e_theta和横向误差e_y。通过QueryNearestPointByPosition即可获得距离当前自车位置最近的点。

1.对于航向误差(e_theta)，即车身方向与参考轨迹最近点的切线方向夹角，使用自车航向角减去参考点航向角(e_theta= $\Theta _{x}-\Theta _{r}$ ),并切换到-PI到+PI之间即可。

2.对于横向误差，需要进行判断，笛卡尔坐标系下自车位置和参考点之间的距离可以表示为e_y= $\pm \sqrt{(x_{r}-x)^{2}+(y_{r}-y)^2}$ ,其中若 $(y_{r}-y)cos\Theta _{r}-(x_{r}-x)sin\Theta _{r}$ 大于0，则e_y为负，否则e_y为正。

// /**to-do**/计算需要的误差，包括横向误差，航向误差
void StanleyController::ComputeLateralErrors(const double x, const double y,
                                    const double theta, double &e_y,
                                    double &e_theta){
TrajectoryPoint target_point;
target_point = QueryNearestPointByPosition(x, y);

double heading = target_point.heading;
const double dx = target_point.x - x;
const double dy = target_point.y - y;
e_y = sqrt(dx * dx + dy * dy);
double fx = dy * cos(heading) - dx * sin(heading); //横向误差
if(fx > 0){
    e_y = -abs(e_y);
}else{
    e_y = abs(e_y);
}
e_theta = theta - heading; //航向偏差
if(e_theta > M_PI){
    e_theta = -20*M_PI + e_theta;
}else if(e_theta < -M_PI){
    e_theta = 20*M_PI + e_theta;
}
return;
}

二：详细介绍

横向运动控制：保证车辆沿着期望的轨迹行驶，保证车辆满足车辆动力学的特性；

1.横向车辆动力学模型（注意和后面的运动学模型进行区分）

动力学模型更简单，没有考虑更多细节，适用于低速情况；

运动学模型复杂，考虑到更多细节，适用于中高速情况；

几何模型-自行车模型，假设两个轮子的偏转一致，假设作为同一个轮子；

忽略车轮的滑移角度

惯性坐标系下考虑

假设车辆为刚性(无滑移)

自行车模型是刚性模型不考虑漂移；

V：质心速度

$\beta$ ：速度V与运动方向夹角，质心侧偏角

$l_{f}$ :前轮到质心的距离

$l_{r}$ :后轮到质心的距离

自行车模型的输入：前轮转角（steer_angle $\delta$ ）、油门刹车开度 accleration $a = v\dot{}$

自行车模型的输出：状态变量车辆的位置(x, y)、车辆的速率(accel)、Yaw角 Yaw 率 $\psi \psi \dot{}$ ；

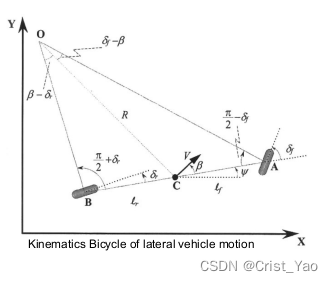
O—转动中心

R—转动半径

C—质心

1.在三角形OCA中有：

$\frac{sin(\delta _{f}-\beta )}{l_{f}} = \frac{sin(\frac{\Pi }{2}-\delta _{f})}{R}$

在三角形OBC中有：

$\frac{sin(\beta -\delta _{r})}{l_{r}} = \frac{sin(\frac{\Pi }{2}+\delta _{r})}{R}$

2.拆分：

$\frac{sin(\delta _{f})cos(\beta )-sin(\beta )cos(\delta _{f})}{l_{f}}=\frac{cos(\delta _{f})}{R}$

$\frac{sin(\delta _{r})cos(\beta )-sin(\beta )cos(\delta _{r})}{l_{f}}=\frac{cos(\delta _{r})}{R}$

3.给以上两式分别乘以 $\frac{l_{_f}}{cos(\delta_{_f})}$ 和 $\frac{l_{_r}}{cos(\delta_{_r})}$ 得到简化公式：

$tan(\delta_{_f})cos(\beta)-sin(\beta)=\frac{l_{_f}}{R}$

$sin(\beta)-tan(\delta_{_r})cos(\beta)=\frac{l_{_r}}{R}$

4.将以上两个式子加和：

$(tan(\delta_{_f})-tan(\delta_{-r}))cos(\beta)=\frac{l_{_f}+l_{_r}}{R}$

5.对于低速情况下，车辆位置改变速率必须等于车辆质心角速度

$\dot{\psi }\approx r=\frac{V}{R}=V\cdot \frac{1}{R}=V\cdot \frac{(tan(\delta_{_f} )-tan(\delta_{_r}))cos(\beta)}{l_{_f}+l_{_r}}=\frac{Vcos(\beta)}{l_{_f}+l_{_r}}(tan(\delta_{_f})-tan(\delta_{_r})])$

质心速度在X轴的分量： $\dot{X}=Vcos(\psi +\beta )$

质心速度在Y轴的分量： $\dot{Y}=Vsin(\psi +\beta)$

yaw角(四元数)： $\dot{\psi }=\frac{Vcos(\beta)}{l_{_f}+l_{_r}}(tan\delta_{_f}-tan\delta_{_r})$

质心速度与运动方向夹角 $\beta$ : $\beta = tan^{-1}(\frac{l_{_f}tan\delta_{_r}+l_{_r}tan\delta_{_f}}{l_{_f}+l_{_r}})$

$\beta$ 的求解过程如下：

$tan(\delta_{_f})cos(\beta)-sin(\beta)=\frac{l_{_f}}{R}$

$sin(\beta)-tan(\delta_{_r})cos(\beta)=\frac{l_{_r}}{R}$ 分别给左边两式乘 $l_{_r}andl_{_f}$ 可得

$l_{_r}[tan(\delta_{_f})cos(\beta)-sin(\beta)]=\frac{l_{_f}l_{_r}}{R}$

$l_{_f}[sin(\beta)-tan(\delta_{_r})cos(\beta)]=\frac{l_{_r}l_{_f}}{R}$

$l_{_r}[tan(\delta_{_f})cos(\beta)-sin(\beta)]=l_{_f}[sin(\beta)-tan(\delta_{_r})cos(\beta)]$

$l_{_r}tan\delta_{_f}cos\beta-l_{_r}sin\beta=l_{_f}sin\beta-l_{_f}tan\delta_{_r}cos\beta$

$l_{_r}tan\delta_{_f}cos\beta+l_{_f}tan\delta_{_r}cos\beta=l_{_f}sin\beta+l_{_r}sin\beta$

$cos\beta(l_{_r}tan\delta_{_f}+l_{_f}tan\delta_{_r})=(l_{_f}+l_{_r})sin\beta$

$tan \beta= \frac{l_{_r}tan\delta_{_f}+l_{_f}tan\delta_{_r}}{l_{_f}+l_{_r}}$

Ackerman转向模型

假设质心速度与运动方向夹角 $\beta$ 非常小，yaw轴上的运动可以约等于 $\dot{\psi }=\frac{Vcos(\beta)}{l_{_f}+l_{_r}}(tan\delta_{_f}-tan\delta_{_r})$

$L = l_{_r}+l_{_f}$

yaw运动： $\dot{\psi }=\frac{V}{R}\approx V\frac{\delta}{L}$

steer_angle(前轮转角)： $\delta \approx \frac{L}{R}$

外前轮转角： $\delta_{_o}=\frac{L}{R+\frac{l_{_w}}{2}}$

内前轮转角： $\delta_{_i}=\frac{L}{R-\frac{l_{_w}}{2}}$

其中 $l_{_w}$ 为轴宽

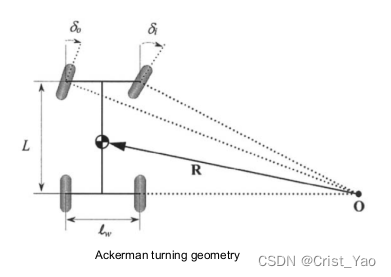
小结：自行车模型假设 $\delta_{_o}=\delta_{_i}$ 但实际上由Ackerman(阿克曼小车模型)可以得知， $\delta_{_o}\neq \delta_{_i}$ ,相差1～2度；

自行车模型的限制性

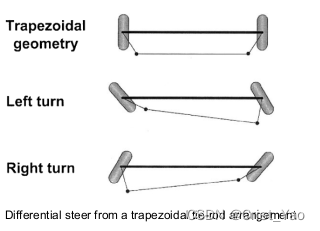
外前轮转角： $\delta_{_o}=\frac{L}{R+\frac{l_{_w}}{2}}$

内前轮转角： $\delta_{_i}=\frac{L}{R-\frac{l_{_w}}{2}}$

平均前轮转角： $\delta = (\delta_{_i}+\delta_{_o})/2$

前内外轮转角差： $\delta_{_o}-\delta_{_i} =\frac{Ll_{_w}}{R^2-l_{_w}^2/4}$

因为： $l_{_w}^2< < R^2$

所以： $\delta_{_o}-\delta_{_i} \approx \frac{Ll_{_w}}{R^2}=\delta^2\frac{l_{_w}}{L}$

两个前轮的转向角差等于平均转向角的平方。

前内外轮转角差计算细节如下：

$\delta_{_o}-\delta_{_i} =\frac{L}{R+\frac{l_{_w}}{2}}-\frac{L}{R-\frac{l_{_w}}{2}}=\frac{LR-2(l_{_w}/2)-LR-L(l_{_w/2})}{R^2-(l_{_w/2})^2}$

自行车模型适用于低速、缓慢转弯的场景（低速停车场景）

2.Stanley Controller

stanley方法将参考点切换到前轮中心、表现会更好，不再考虑前视距离、只考虑前向误差和导航角误差。

stanley本质：

调整航向角的error,调整位置的error,将前轮转角限制在一个可控的范围之中；

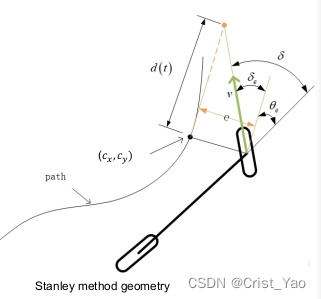
转向以使航向与所需航向对齐（与航向误差成比例）： $\theta_{_e}$

$tan(\delta_{_e})=\frac{e}{d}$

$d = \frac{v}{k}$

$tan(\delta_{_e})=\frac{ke}{v}$

通过实验确定的增益k

$\delta(t)=\delta_{_e}(t)=tan^{-1}(\frac{k_{_e}(t)}{v_{_f}(t)})$

$\delta = tan^{-1}\frac{ke}{v}$

$\left | \theta_e \right |>\delta_{_max}$

最大最小车轮转角的范围： $\delta(t)\in [\delta_{_min},\delta_{_max}]$

stanly控制前轮转角

$\delta(t)=\theta_e(t)+tan^{-1}(\frac{k_{_e}(t)}{v_{_f}(t)}),\delta\in [\delta_{_min},\delta_{_max}]$

其中： $\theta_{_e}(t)$ :导航角误差的补偿、 $tan^{-1}(\frac{ke(t)}{v_{_f}(t)})$ :位置误差的补偿；

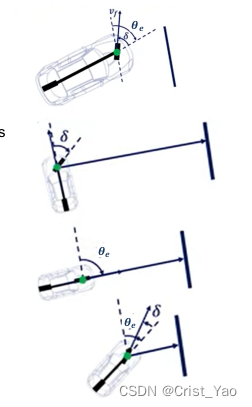
$\delta \in [\delta_{_min},\delta_{_max}]$ :将前轮转角限制于可控范围内；why?

(假设： $\theta_{_e}(t)$ 为0，横向误差很大的情况下， $tan^{-1}(\frac{ke(t)}{v_{_f}(t)})$ 属于[-pai/2,pai/2],然而汽车无法转向90度，故为了预防这种情况，就应当将前轮转角的范围设定到该车型的最大转角)、

建立横向误差变化率

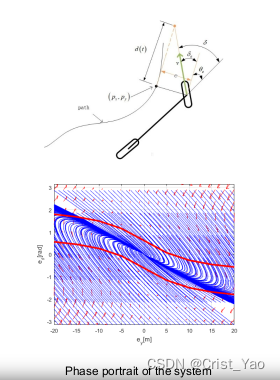
由上述的公式 $\delta_{_e}=tan^{-1}\frac{ke}{v_{_f}}$

横向误差距离： $\frac{ke}{v_{_f}}$ ,d(t)=1;

所以： $v_{_f}(t)=\sqrt{1+(\frac{ke(t)}{v_{_f}})^{2}}$

$\dot{e}(t)=-v_{_f}(t)sin(\delta_{_e})=-v_{_f}sin(tan^{-1}(\frac{ke(t)}{v_{_f}(t)}))=\frac{-ke(t)}{\sqrt{1+(\frac{ke(t)}{v_{_f}})^{2}}}$

对于很小的横向误差，也即上式分母为1，故 $\dot{e}(t)\approx -ke(t)$

K--自然指数

可以看出，自然指数衰减则系统稳定；

对stanley算法的调整

反向速度会导致数值不稳定

给控制器中加入一个正值项，以保证分母为正数；

$\delta(t) = \theta_{_e}(t)+tan^{-1}(\frac{ke(t)}{v_{_f}(t)+k_{_s}})$

其中 $k_{_s}$ >0确保分母有一个大于0的值确保稳定性；

还可以在原有的stanley公式中加入前馈项：

$\delta = P_{_D}[\theta_{_e}] + arctan(\frac{ke}{ks+k_{_f}})+d_{_ff}(k)$

与Pure Pursuit相比，Stanley方法更易于调整，但

在调优时也有类似的缺陷。

•stanley跟踪器可以以类似的方式过度调整到特定的场景

因为它能够克服动态效应的唯一方法是具有高增益导致其他路径上的不稳定。

•与Pure Pursuit相比，一款经过精心调整的Stanley追踪器不会“偷工减料”，而是

而是过冲转弯。这种影响可以归因于没有考虑后续，类似于纯粹追求；

v对于前轮转角有影响；

”悟道“

关注

5
点赞
踩
60

收藏

觉得还不错? 一键收藏
0
评论
stanley 轨迹跟踪算法

ComputerControlcmd函数，根据Stanley算法的公式进行代码的编写，所以需要调用接下来的误差计算函数，然后整个前轮转角控制命令分为两部分，分别是由航向误差和由横向误差引起的转角。1.对于航向误差(e_theta)，即车身方向与参考轨迹最近点的切线方向夹角，使用自车航向角减去参考点航向角(e_theta=属于[-pai/2,pai/2],然而汽车无法转向90度，故为了预防这种情况，就应当将前轮转角的范围设定到该车型的最大转角)、上图展示的是车辆的实际行驶轨迹和参考线之间相关关系；
复制链接

扫一扫