1、状态空间模型
线性离散时间系统的状态空间模型如下:
x
(
k
+
1
)
=
A
x
(
k
)
+
B
u
u
(
k
)
+
B
d
d
(
k
)
y
c
(
k
)
=
C
c
x
(
k
)
(1)
\begin{aligned} &x(k+1)=Ax(k)+B_uu(k)+B_dd(k)\\[1ex] &y_c(k)=C_cx(k)\tag{1} \end{aligned}
x(k+1)=Ax(k)+Buu(k)+Bdd(k)yc(k)=Ccx(k)(1)
其中 x ( k ) ∈ R n x x(k)\in\cal{R}^{n_x} x(k)∈Rnx 是状态变量; u ( k ) ∈ R n u u(k)\in\cal{R}^{n_u} u(k)∈Rnu 是控制输入变量; y c ( k ) ∈ R n c y_c(k)\in\cal{R}^{n_c} yc(k)∈Rnc 是被控输出变量; d ( k ) ∈ R n d d(k)\in\cal{R}^{n_d} d(k)∈Rnd 是可以测量的外部干扰变量。
上面的离散时间模型与连续时间模型
x ˙ = A c x ( t ) + B c u u ( t ) + B c d d ( t ) y c ( t ) = C c x ( t ) (2) \begin{aligned} &\dot{x}=A_cx(t)+B_{cu}u(t)+B_{cd}d(t)\\[1ex] &y_c(t)=C_cx(t)\tag{2} \end{aligned} x˙=Acx(t)+Bcuu(t)+Bcdd(t)yc(t)=Ccx(t)(2)
之间有如下的转化关系:
A = e A c T s B u = ∫ 0 T s e A c τ d τ ⋅ B c u B d = ∫ 0 T s e A c τ d τ ⋅ B c d (3) \begin{aligned} A&=e^{A_cT_s}\\[1ex] B_u&=\int_0^{T_s}e^{A_c\tau}\mathrm{d}\tau\cdot B_{cu}\\[1ex] B_d&=\int_0^{T_s}e^{A_c\tau}\mathrm{d}\tau\cdot B_{cd} \end{aligned}\tag{3} ABuBd=eAcTs=∫0TseAcτdτ⋅Bcu=∫0TseAcτdτ⋅Bcd(3)
其中 T s T_s Ts 是系统的采样时间。
2、预测方程
将模型(1)改写成增量模型
Δ
x
(
k
+
1
)
=
A
Δ
x
(
k
)
+
B
u
Δ
u
(
k
)
+
B
d
Δ
d
(
k
)
y
c
(
k
)
=
C
c
Δ
x
(
k
)
+
y
c
(
k
−
1
)
(4)
\begin{aligned} \Delta x(k+1)&=A\Delta x(k) + B_u\Delta u(k) + B_d\Delta d(k)\\[1ex] y_c(k)&=C_c\Delta x(k)+y_c(k-1)\tag{4} \end{aligned}
Δx(k+1)yc(k)=AΔx(k)+BuΔu(k)+BdΔd(k)=CcΔx(k)+yc(k−1)(4)
其中
Δ
x
(
k
)
=
x
(
k
)
−
x
(
k
−
1
)
Δ
u
(
k
)
=
u
(
k
)
−
u
(
k
−
1
)
Δ
d
(
k
)
=
d
(
k
)
−
d
(
k
−
1
)
\begin{aligned} \Delta x(k)=x(k)-x(k-1)\\[1ex] \Delta u(k)=u(k)-u(k-1)\\[1ex] \Delta d(k)=d(k)-d(k-1)\\[1ex] \end{aligned}
Δx(k)=x(k)−x(k−1)Δu(k)=u(k)−u(k−1)Δd(k)=d(k)−d(k−1)
首先以最新测量值为初始条件,基于模型(4)预测系统未来的动态。为此,设定预测时域为 p p p,控制时域为 m m m 且 m ≤ p m\leq p m≤p。为了推导系统的预测方程,我们假设:
- 控制时域之外,控制量不变,即
Δ
u
(
k
+
i
)
=
0
,
i
=
m
,
m
+
1
,
⋯
,
p
−
1
\Delta u(k+i)=0,\quad i=m,m+1,\cdots,p-1
Δu(k+i)=0,i=m,m+1,⋯,p−1;
该假设是因为控制时域有可能小于预测时域,而预测系统未来动态需要在整个预测时域的控制输入。 - 可测干扰在
k
k
k 时刻之后不变,即
Δ
d
(
k
+
i
)
=
0
,
i
=
1
,
2
,
⋯
,
p
−
1
\Delta d(k+i)=0,\quad i=1,2,\cdots,p-1
Δd(k+i)=0,i=1,2,⋯,p−1;
该假设是因为在当前时刻( k k k 时刻),我们还不知道干扰的未来取值。
在当前时刻
k
k
k,测量值为
x
(
k
)
x(k)
x(k),可以计算
Δ
x
(
k
)
=
x
(
k
)
−
x
(
k
−
1
)
\Delta x(k)=x(k)-x(k-1)
Δx(k)=x(k)−x(k−1),这个将作为预测系统未来动态的起点。由(4)可以预测
k
+
1
k+1
k+1 到
k
+
3
k+3
k+3 时刻的状态(实际上是状态增量,简单起见称为状态)如下:
Δ
x
(
k
+
1
∣
k
)
=
A
Δ
x
(
k
)
+
B
u
Δ
u
(
k
)
+
B
d
Δ
d
(
k
)
Δ
x
(
k
+
2
∣
k
)
=
A
Δ
x
(
k
+
1
∣
k
)
+
B
u
Δ
u
(
k
+
1
)
+
B
d
Δ
d
(
k
+
1
)
=
A
2
Δ
x
(
k
)
+
A
B
u
Δ
u
(
k
)
+
B
u
Δ
u
(
k
+
1
)
+
A
B
d
Δ
d
(
k
)
Δ
x
(
k
+
3
∣
k
)
=
A
Δ
x
(
k
+
2
∣
k
)
+
B
u
Δ
u
(
k
+
2
)
+
B
d
Δ
d
(
k
+
2
)
=
A
3
Δ
x
(
k
)
+
A
2
B
u
Δ
u
(
k
)
+
A
B
u
Δ
u
(
k
+
1
)
+
B
u
Δ
u
(
k
+
2
)
+
A
2
B
d
Δ
d
(
k
)
(5)
\begin{aligned} \Delta x(k+1|k)&=A\Delta x(k) + B_u\Delta u(k) + B_d\Delta d(k)\\[1ex] \Delta x(k+2|k)&=A\Delta x(k+1|k) + B_u\Delta u(k+1) + B_d\Delta d(k+1)\\[1ex] &=A^2\Delta x(k) + AB_u\Delta u(k) + B_u\Delta u(k+1) + AB_d\Delta d(k)\\[1ex] \Delta x(k+3|k)&=A\Delta x(k+2|k) + B_u\Delta u(k+2) + B_d\Delta d(k+2)\\[1ex] &=A^3\Delta x(k) + A^2B_u\Delta u(k) + AB_u\Delta u(k+1) + B_u\Delta u(k+2) + A^2B_d\Delta d(k)\tag{5} \end{aligned}
Δx(k+1∣k)Δx(k+2∣k)Δx(k+3∣k)=AΔx(k)+BuΔu(k)+BdΔd(k)=AΔx(k+1∣k)+BuΔu(k+1)+BdΔd(k+1)=A2Δx(k)+ABuΔu(k)+BuΔu(k+1)+ABdΔd(k)=AΔx(k+2∣k)+BuΔu(k+2)+BdΔd(k+2)=A3Δx(k)+A2BuΔu(k)+ABuΔu(k+1)+BuΔu(k+2)+A2BdΔd(k)(5)
式中,
k
+
1
∣
k
k+1|k
k+1∣k 表示
k
k
k 时刻对
k
+
1
k+1
k+1 时刻的预测;符号
∣
|
∣ 后面的
k
k
k 表示当前时刻为
k
k
k。进而,可以预测
k
+
m
k+m
k+m 至
k
+
p
k+p
k+p 时刻的状态
Δ
x
(
k
+
m
∣
k
)
=
A
Δ
x
(
k
+
m
−
1
∣
k
)
+
B
u
Δ
u
(
k
+
m
−
1
)
+
B
d
Δ
d
(
k
+
m
−
1
)
=
A
m
Δ
x
(
k
)
+
A
m
−
1
B
u
Δ
u
(
k
)
+
A
m
−
2
B
u
Δ
u
(
k
+
1
)
+
⋯
+
B
u
Δ
u
(
k
+
m
−
1
)
+
A
m
−
1
B
d
Δ
d
(
k
)
⋮
Δ
x
(
k
+
p
∣
k
)
=
A
Δ
x
(
k
+
p
−
1
∣
k
)
+
B
u
Δ
u
(
k
+
p
−
1
)
+
B
d
Δ
d
(
k
+
p
−
1
)
=
A
p
Δ
x
(
k
)
+
A
p
−
1
B
u
Δ
u
(
k
)
+
A
p
−
2
B
u
Δ
u
(
k
+
1
)
+
⋯
+
A
p
−
m
B
u
Δ
u
(
k
+
m
−
1
)
+
A
p
−
1
B
d
Δ
d
(
k
)
(6)
\begin{aligned} \Delta x(k+m|k)&=A\Delta x(k+m-1|k) + B_u\Delta u(k+m-1) + B_d\Delta d(k+m-1)\\[1ex] &=A^m\Delta x(k) + A^{m-1}B_u\Delta u(k) + A^{m-2}B_u\Delta u(k+1) +\cdots + B_u\Delta u(k+m-1) + A^{m-1}B_d\Delta d(k)\\[1ex] &\vdots\\[1ex] \Delta x(k+p|k)&=A\Delta x(k+p-1|k) + B_u\Delta u(k+p-1) + B_d\Delta d(k+p-1)\\[1ex] &=A^p\Delta x(k) + A^{p-1}B_u\Delta u(k) + A^{p-2}B_u\Delta u(k+1) +\cdots + A^{p-m}B_u\Delta u(k+m-1) + A^{p-1}B_d\Delta d(k)\\[1ex] \end{aligned}\tag{6}
Δx(k+m∣k)Δx(k+p∣k)=AΔx(k+m−1∣k)+BuΔu(k+m−1)+BdΔd(k+m−1)=AmΔx(k)+Am−1BuΔu(k)+Am−2BuΔu(k+1)+⋯+BuΔu(k+m−1)+Am−1BdΔd(k)⋮=AΔx(k+p−1∣k)+BuΔu(k+p−1)+BdΔd(k+p−1)=ApΔx(k)+Ap−1BuΔu(k)+Ap−2BuΔu(k+1)+⋯+Ap−mBuΔu(k+m−1)+Ap−1BdΔd(k)(6)
进一步,由增量方程(4)可以预测
k
+
1
k+1
k+1 至
k
+
p
k+p
k+p 的被控输出
y
c
(
k
+
1
∣
k
)
=
C
c
Δ
x
(
k
+
1
∣
k
)
+
y
c
(
k
)
=
C
c
A
Δ
x
(
k
)
+
C
c
B
u
Δ
u
(
k
)
+
C
c
B
d
Δ
d
(
k
)
+
y
c
(
k
)
,
y
c
(
k
+
2
∣
k
)
=
C
c
Δ
x
(
k
+
2
∣
k
)
+
y
c
(
k
+
1
∣
k
)
=
(
C
c
A
2
+
C
c
A
)
Δ
x
(
k
)
+
(
C
c
A
B
u
+
C
c
B
u
)
Δ
u
(
k
)
+
C
c
B
u
Δ
u
(
k
+
1
)
+
(
C
c
A
B
d
+
C
c
B
d
)
Δ
d
(
k
)
+
y
c
(
k
)
,
⋮
y
c
(
k
+
m
∣
k
)
=
C
c
Δ
x
(
k
+
m
∣
k
)
+
y
c
(
k
+
m
−
1
∣
k
)
=
∑
i
=
1
m
C
c
A
i
Δ
x
(
k
)
+
∑
i
=
1
m
C
c
A
i
−
1
B
u
Δ
u
(
k
)
+
∑
i
=
1
m
−
1
C
c
A
i
−
1
B
u
Δ
u
(
k
+
1
)
+
⋯
+
C
c
B
u
Δ
u
(
k
+
m
−
1
)
+
∑
i
=
1
m
C
c
A
i
−
1
B
d
Δ
d
(
k
)
+
y
c
(
k
)
,
⋮
y
c
(
k
+
p
∣
k
)
=
C
c
Δ
x
(
k
+
p
∣
k
)
+
y
c
(
k
+
p
−
1
∣
k
)
=
∑
i
=
1
p
C
c
A
i
Δ
x
(
k
)
+
∑
i
=
1
p
C
c
A
i
−
1
B
u
Δ
u
(
k
)
+
∑
i
=
1
p
−
1
C
c
A
i
−
1
B
u
Δ
u
(
k
+
1
)
+
⋯
+
∑
i
=
1
p
−
m
+
1
C
c
A
i
−
1
B
u
Δ
u
(
k
+
m
−
1
)
+
∑
i
=
1
p
C
c
A
i
−
1
B
d
Δ
d
(
k
)
+
y
c
(
k
)
,
(7)
\begin{aligned} y_c(k+1|k)&=C_c\Delta x(k+1|k)+y_c(k)\\[1ex] &=C_cA\Delta x(k)+C_cB_u\Delta u(k)+C_cB_d\Delta d(k)+y_c(k),\\[1ex] y_c(k+2|k)&=C_c\Delta x(k+2|k)+y_c(k+1|k)\\[1ex] &=(C_cA^2+C_cA)\Delta x(k)+(C_cAB_u+C_cB_u)\Delta u(k)\\[1ex]&\quad+C_cB_u\Delta u(k+1)+(C_cAB_d+C_cB_d)\Delta d(k)+y_c(k),\\[1ex] &\vdots\\[1ex] y_c(k+m|k)&=C_c\Delta x(k+m|k)+y_c(k+m-1|k)\\[1ex] &=\sum_{i=1}^mC_cA^i\Delta x(k)+\sum_{i=1}^mC_cA^{i-1}B_u\Delta u(k)+\sum_{i=1}^{m-1}C_cA^{i-1}B_u\Delta u(k+1)+\cdots\\[1ex]&\quad+C_cB_u\Delta u(k+m-1)+\sum_{i=1}^mC_cA^{i-1}B_d\Delta d(k)+y_c(k),\\[1ex] &\vdots\\[1ex] y_c(k+p|k)&=C_c\Delta x(k+p|k)+y_c(k+p-1|k)\\[1ex] &=\sum_{i=1}^pC_cA^i\Delta x(k)+\sum_{i=1}^pC_cA^{i-1}B_u\Delta u(k)+\sum_{i=1}^{p-1}C_cA^{i-1}B_u\Delta u(k+1)+\cdots\\[1ex]&\quad+\sum_{i=1}^{p-m+1}C_cA^{i-1}B_u\Delta u(k+m-1)+\sum_{i=1}^pC_cA^{i-1}B_d\Delta d(k)+y_c(k),\\[1ex] \end{aligned}\tag{7}
yc(k+1∣k)yc(k+2∣k)yc(k+m∣k)yc(k+p∣k)=CcΔx(k+1∣k)+yc(k)=CcAΔx(k)+CcBuΔu(k)+CcBdΔd(k)+yc(k),=CcΔx(k+2∣k)+yc(k+1∣k)=(CcA2+CcA)Δx(k)+(CcABu+CcBu)Δu(k)+CcBuΔu(k+1)+(CcABd+CcBd)Δd(k)+yc(k),⋮=CcΔx(k+m∣k)+yc(k+m−1∣k)=i=1∑mCcAiΔx(k)+i=1∑mCcAi−1BuΔu(k)+i=1∑m−1CcAi−1BuΔu(k+1)+⋯+CcBuΔu(k+m−1)+i=1∑mCcAi−1BdΔd(k)+yc(k),⋮=CcΔx(k+p∣k)+yc(k+p−1∣k)=i=1∑pCcAiΔx(k)+i=1∑pCcAi−1BuΔu(k)+i=1∑p−1CcAi−1BuΔu(k+1)+⋯+i=1∑p−m+1CcAi−1BuΔu(k+m−1)+i=1∑pCcAi−1BdΔd(k)+yc(k),(7)
定义
p
p
p 步预测输出向量和
m
m
m 步输入向量如下:
Y
p
(
k
+
1
∣
k
)
=
=
d
e
f
[
y
c
(
k
+
1
∣
k
)
y
c
(
k
+
2
∣
k
)
⋮
y
c
(
k
+
p
∣
k
)
]
p
×
1
,
Δ
U
(
k
)
=
=
d
e
f
[
Δ
u
(
k
)
Δ
u
(
k
+
1
)
⋮
Δ
u
(
k
+
m
−
1
)
]
m
×
1
(8)
\begin{aligned} Y_p(k+1|k)&\overset{\mathrm{def}}{=\!=}\left[ \begin{matrix} y_c(k+1|k) \\[2ex] y_c(k+2|k) \\[2ex] \vdots\\[2ex] y_c(k+p|k) \end{matrix} \right]_{p\times 1},\\[1ex] \Delta U(k)&\overset{\mathrm{def}}{=\!=}\left[ \begin{matrix} \Delta u(k) \\[2ex] \Delta u(k+1) \\[2ex] \vdots\\[2ex] \Delta u(k+m-1) \end{matrix} \right]_{m\times 1} \end{aligned}\tag{8}
Yp(k+1∣k)ΔU(k)==def
yc(k+1∣k)yc(k+2∣k)⋮yc(k+p∣k)
p×1,==def
Δu(k)Δu(k+1)⋮Δu(k+m−1)
m×1(8)
那么,对系统未来
p
p
p 步预测的输出可以由下面的预测方程计算:
Y
p
(
k
+
1
∣
k
)
=
S
x
Δ
x
(
k
)
+
I
y
c
(
k
)
+
S
d
Δ
d
(
k
)
+
S
u
Δ
U
(
k
)
(9)
Y_p(k+1|k)=S_x\Delta x(k)+{\cal{I}}y_c(k)+{\cal{S}_d}\Delta d(k)+{\cal{S}_u}\Delta U(k)\tag{9}
Yp(k+1∣k)=SxΔx(k)+Iyc(k)+SdΔd(k)+SuΔU(k)(9)
其中
S
x
=
[
C
c
A
∑
i
=
1
2
C
c
A
i
⋮
∑
i
=
1
p
C
c
A
i
]
p
×
1
,
I
=
[
I
n
c
×
n
c
I
n
c
×
n
c
⋮
I
n
c
×
n
c
]
p
×
1
,
S
d
=
[
C
c
B
d
∑
i
=
1
2
C
c
A
i
−
1
B
d
⋮
∑
i
=
1
p
C
c
A
i
−
1
B
d
]
p
×
1
,
S
u
=
[
C
c
B
u
0
0
⋯
0
∑
i
=
1
2
C
c
A
i
−
1
B
u
C
c
B
u
0
⋯
0
⋮
⋮
⋮
⋮
∑
i
=
1
m
C
c
A
i
−
1
B
u
∑
i
=
1
m
−
1
C
c
A
i
−
1
B
u
⋯
⋯
C
c
B
u
⋮
⋮
⋮
⋮
∑
i
=
1
p
C
c
A
i
−
1
B
u
∑
i
=
1
p
−
1
C
c
A
i
−
1
B
u
⋯
⋯
∑
i
=
1
p
−
m
+
1
C
c
A
i
−
1
B
u
]
p
×
m
(10)
\begin{aligned} S_x&=\left[ \begin{matrix} C_cA \\[2ex] \sum_{i=1}^2C_cA^i \\[2ex] \vdots\\[2ex] \sum_{i=1}^pC_cA^i \end{matrix} \right]_{p\times 1} ,\quad{\cal{I}}=\left[ \begin{matrix} I_{n_c\times n_c} \\[1ex] I_{n_c\times n_c} \\[1ex] \vdots\\[1ex] I_{n_c\times n_c} \end{matrix} \right]_{p\times 1},\quad{\cal{S}_d}=\left[ \begin{matrix} C_cB_d \\[2ex] \sum_{i=1}^2C_cA^{i-1}B_d \\[2ex] \vdots\\[2ex] \sum_{i=1}^pC_cA^{i-1}B_d \end{matrix} \right]_{p\times 1},\\[4ex] {\cal{S}_u}&=\left[ \begin{matrix} C_cB_u & 0 & 0 & \cdots & 0\\[2ex] \sum_{i=1}^2C_cA^{i-1}B_u & C_cB_u & 0 & \cdots & 0 \\[2ex] \vdots & \vdots & \vdots & &\vdots \\[2ex] \sum_{i=1}^mC_cA^{i-1}B_u & \sum_{i=1}^{m-1}C_cA^{i-1}B_u & \cdots & \cdots & C_cB_u \\[2ex] \vdots & \vdots & \vdots & &\vdots \\[2ex] \sum_{i=1}^pC_cA^{i-1}B_u & \sum_{i=1}^{p-1}C_cA^{i-1}B_u & \cdots & \cdots & \sum_{i=1}^{p-m+1}C_cA^{i-1}B_u \end{matrix} \right]_{p\times m} \end{aligned}\tag{10}
SxSu=
CcA∑i=12CcAi⋮∑i=1pCcAi
p×1,I=
Inc×ncInc×nc⋮Inc×nc
p×1,Sd=
CcBd∑i=12CcAi−1Bd⋮∑i=1pCcAi−1Bd
p×1,=
CcBu∑i=12CcAi−1Bu⋮∑i=1mCcAi−1Bu⋮∑i=1pCcAi−1Bu0CcBu⋮∑i=1m−1CcAi−1Bu⋮∑i=1p−1CcAi−1Bu00⋮⋯⋮⋯⋯⋯⋯⋯00⋮CcBu⋮∑i=1p−m+1CcAi−1Bu
p×m(10)
3、无约束预测控制
3.1、开环优化问题的数学描述
目标函数的选取反映了对系统性能的要求,如果希望被控输出接近参考输入,则可选取如下的最简单形式:
J
=
∑
i
=
1
p
∑
j
=
1
n
c
(
Γ
y
j
(
y
c
j
(
k
+
i
∣
k
)
−
r
j
(
k
+
i
)
)
)
2
(11)
J=\sum_{i=1}^p\sum_{j=1}^{n_c}\Big(\Gamma_{y_j}\big(y_{cj}(k+i|k)-r_j(k+i)\big)\Big)^2\tag{11}
J=i=1∑pj=1∑nc(Γyj(ycj(k+i∣k)−rj(k+i)))2(11)
其中
r
j
(
k
+
i
)
,
i
=
1
,
2
,
⋯
,
p
r_j(k+i),i=1,2,\cdots,p
rj(k+i),i=1,2,⋯,p 为给定的参考输入序列的第
j
j
j 个分量;
Γ
y
j
\Gamma_{y_j}
Γyj 是对第
j
j
j 个预测控制输出误差的加权因子。加权因子越大,表明我们期望对应的控制输出越接近给定的参考输入。在整个预测时域中,加权因子也可以不一样,即采用时变加权因子,目标函数如下:
J
=
∑
i
=
1
p
∑
j
=
1
n
c
(
Γ
y
j
,
i
(
y
c
j
(
k
+
i
∣
k
)
−
r
j
(
k
+
i
)
)
)
2
=
∑
i
=
1
p
∥
Γ
y
,
i
(
y
c
(
k
+
i
∣
k
)
−
r
(
k
+
i
)
)
∥
2
(12)
\begin{aligned} J&=\sum_{i=1}^p\sum_{j=1}^{n_c}\Big(\Gamma_{y_j,i}\big(y_{cj}(k+i|k)-r_j(k+i)\big)\Big)^2\\[1ex] &=\sum_{i=1}^p\parallel\Gamma_{y,i}\big(y_{c}(k+i|k)-r(k+i)\big)\parallel^2 \tag{12} \end{aligned}
J=i=1∑pj=1∑nc(Γyj,i(ycj(k+i∣k)−rj(k+i)))2=i=1∑p∥Γy,i(yc(k+i∣k)−r(k+i))∥2(12)
其中
Γ
y
j
,
i
\Gamma_{y_j,i}
Γyj,i 是在预测时刻
i
i
i 对预测控制输出第
j
j
j 个分量误差的加权因子,以及
Γ
y
j
,
i
=
=
d
e
f
d
i
a
g
(
Γ
y
1
,
i
,
Γ
y
2
,
i
,
⋯
,
Γ
y
n
c
,
i
)
\Gamma_{y_j,i}\overset{\mathrm{def}}{=\!=}\mathrm{diag}(\Gamma_{y_1,i},\Gamma_{y_2,i},\cdots,\Gamma_{y_{n_c},i})
Γyj,i==defdiag(Γy1,i,Γy2,i,⋯,Γync,i)
经常地,我们还希望控制动作变化不要太大,即采用如下目标函数:
J
=
∑
i
=
1
p
∥
Γ
y
,
i
(
y
c
(
k
+
i
∣
k
)
−
r
(
k
+
i
)
)
∥
2
+
∑
i
=
1
m
∥
Γ
u
,
i
Δ
u
(
k
+
i
−
1
)
∥
2
(13)
J=\sum_{i=1}^p\parallel\Gamma_{y,i}\big(y_c(k+i|k)-r(k+i)\big)\parallel^2+\sum_{i=1}^m\parallel\Gamma_{u,i}\Delta u(k+i-1)\parallel^2\tag{13}
J=i=1∑p∥Γy,i(yc(k+i∣k)−r(k+i))∥2+i=1∑m∥Γu,iΔu(k+i−1)∥2(13)
其中
Γ
u
,
i
=
=
d
e
f
d
i
a
g
(
Γ
u
1
,
i
,
Γ
u
2
,
i
,
⋯
,
Γ
u
n
u
,
i
)
\Gamma_{u,i}\overset{\mathrm{def}}{=\!=}\mathrm{diag}(\Gamma_{u_1,i},\Gamma_{u_2,i},\cdots,\Gamma_{u_{n_u},i})
Γu,i==defdiag(Γu1,i,Γu2,i,⋯,Γunu,i)
且 Γ u j , i \Gamma_{u_j,i} Γuj,i 是在预测时刻 i i i 对控制增量的第 j j j 个分量的加权因子,控制加权因子 Γ u , i \Gamma_{u,i} Γu,i 越大,表明我们期望对应的控制动作变化越小。因此,开环优化问题可以描述如下。
min Δ U ( k ) J ( x ( k ) , Δ U ( k ) , m , p ) (14) \min_{\Delta U(k)}J\big(x(k),\Delta U(k),m,p\big)\tag{14} ΔU(k)minJ(x(k),ΔU(k),m,p)(14)
满足系统动力学 ( i = 0 , 1 , ⋯ , p ) (i=0,1,\cdots,p) (i=0,1,⋯,p)
Δ x ( k + i + 1 ∣ k ) = A Δ x ( k + i ∣ k ) + B u Δ u ( k + i ) + B d Δ d ( k + i ) Δ x ( k ∣ k ) = Δ x ( k ) y c ( k + i ∣ k ) = C c Δ x ( k + i ∣ k ) + y c ( k + i − 1 ∣ k ) (15) \begin{aligned} \Delta x(k+i+1|k)&=A\Delta x(k+i|k)+B_u\Delta u(k+i)+B_d\Delta d(k+i)\\[1ex] \Delta x(k|k)&=\Delta x(k)\\[1ex] y_c(k+i|k)&=C_c\Delta x(k+i|k)+y_c(k+i-1|k) \end{aligned}\tag{15} Δx(k+i+1∣k)Δx(k∣k)yc(k+i∣k)=AΔx(k+i∣k)+BuΔu(k+i)+BdΔd(k+i)=Δx(k)=CcΔx(k+i∣k)+yc(k+i−1∣k)(15)其中
J ( x ( k ) , Δ U ( k ) , m , p ) = ∑ i = 1 p ∥ Γ y , i ( y c ( k + i ∣ k ) − r ( k + i ) ) ∥ 2 + ∑ i = 1 m ∥ Γ u , i Δ u ( k + i − 1 ) ∥ 2 (16) J\big(x(k),\Delta U(k),m,p\big)=\sum_{i=1}^p\parallel\Gamma_{y,i}\big(y_c(k+i|k)-r(k+i)\big)\parallel^2+\sum_{i=1}^m\parallel\Gamma_{u,i}\Delta u(k+i-1)\parallel^2\tag{16} J(x(k),ΔU(k),m,p)=i=1∑p∥Γy,i(yc(k+i∣k)−r(k+i))∥2+i=1∑m∥Γu,iΔu(k+i−1)∥2(16)将(16)写成矩阵向量形式,则
J ( x ( k ) , Δ U ( k ) , m , p ) = ∥ Γ y , i ( Y p ( k + 1 ∣ k ) − R ( k + 1 ) ) ∥ 2 + ∥ Γ u Δ U ( k ) ∥ 2 (17) J\big(x(k),\Delta U(k),m,p\big)=\parallel\Gamma_{y,i}\big(Y_p(k+1|k)-R(k+1)\big)\parallel^2+\parallel\Gamma_u\Delta U(k)\parallel^2\tag{17} J(x(k),ΔU(k),m,p)=∥Γy,i(Yp(k+1∣k)−R(k+1))∥2+∥ΓuΔU(k)∥2(17)
其中 Y p ( k + 1 ∣ k ) Y_p(k+1|k) Yp(k+1∣k) 由预测方程(9)给出。上式中,加权矩阵为
Γ y = d i a g ( Γ y , 1 , Γ y , 2 , ⋯ , Γ y , p ) Γ u = d i a g ( Γ u , 1 , Γ u , 2 , ⋯ , Γ u , m ) (18) \begin{aligned} \Gamma_y&=\mathrm{diag}(\Gamma_{y,1},\Gamma_{y,2},\cdots,\Gamma_{y,p})\\[1ex] \Gamma_u&=\mathrm{diag}(\Gamma_{u,1},\Gamma_{u,2},\cdots,\Gamma_{u,m}) \end{aligned}\tag{18} ΓyΓu=diag(Γy,1,Γy,2,⋯,Γy,p)=diag(Γu,1,Γu,2,⋯,Γu,m)(18)参考输入序列为
R ( k + 1 ) = [ r ( k + 1 ) r ( k + 2 ) ⋮ r ( k + p ) ] p × 1 (19) R(k+1)=\left[ \begin{matrix} r(k+1) \\[1ex] r(k+2) \\[1ex] \vdots\\[1ex] r(k+p) \end{matrix} \right]_{p\times 1}\tag{19} R(k+1)= r(k+1)r(k+2)⋮r(k+p) p×1(19)
3.2 开环优化问题的求解
为了方便求解优化问题(14),定义辅助变量
ρ
=
=
d
e
f
[
Γ
y
(
Y
p
(
k
+
1
∣
k
)
−
R
(
k
+
1
)
)
Γ
u
Δ
U
(
k
)
]
(20)
\rho\overset{\mathrm{def}}{=\!=}\left[ \begin{matrix} \Gamma_y\big(Y_p(k+1|k)-R(k+1)\big) \\[1ex] \Gamma_u\Delta U(k) \\[1ex] \end{matrix} \right]\tag{20}
ρ==def[Γy(Yp(k+1∣k)−R(k+1))ΓuΔU(k)](20)
则目标函数(17)变为
J
(
x
(
k
)
,
Δ
U
(
k
)
,
m
,
p
)
=
ρ
T
ρ
(21)
J\big(x(k),\Delta U(k),m,p\big)=\rho^T\rho\tag{21}
J(x(k),ΔU(k),m,p)=ρTρ(21)
将预测方程(9)代入(20),得
ρ
=
[
Γ
y
(
S
x
Δ
x
(
k
)
+
I
y
c
(
k
)
+
S
d
Δ
d
(
k
)
+
S
u
Δ
U
(
k
)
−
R
(
k
+
1
)
)
Γ
u
Δ
U
(
k
)
]
=
[
Γ
y
S
u
Γ
u
]
Δ
U
(
k
)
−
[
Γ
y
(
R
(
k
+
1
)
−
S
x
Δ
x
(
k
)
−
I
y
c
(
k
)
−
S
d
Δ
d
(
k
)
)
⏞
E
p
(
k
+
1
∣
k
)
0
]
=
[
Γ
y
S
u
Γ
u
]
Δ
U
(
k
)
⏟
A
z
−
[
Γ
y
E
p
(
k
+
1
∣
k
)
0
]
⏟
b
=
A
z
−
b
(22)
\begin{aligned} \rho&=\left[ \begin{matrix} \Gamma_y\big(S_x\Delta x(k)+{\cal{I}}y_c(k)+{\cal{S}_d}\Delta d(k)+{\cal{S}_u}\Delta U(k)-R(k+1)\big) \\[1ex] \Gamma_u\Delta U(k) \\[1ex] \end{matrix} \right]\\[1ex] &=\left[ \begin{matrix} \Gamma_y\cal{S}_u \\[1ex] \Gamma_u \\[1ex] \end{matrix} \right]\Delta U(k)- \left[ \begin{matrix} \Gamma_y\overbrace{\big(R(k+1)-\cal{S}_x\Delta x(k)-\cal{I}{y_c}(k)-\cal{S}_d\Delta d(k)\big)}^{E_p(k+1|k)} \\[1ex] 0 \\[1ex] \end{matrix} \right]\\ &= \underbrace{\left[ \begin{matrix} \Gamma_y\cal{S}_u \\[1ex] \Gamma_u \\[1ex] \end{matrix} \right]\Delta U(k)}_{Az}- \underbrace{\left[ \begin{matrix} \Gamma_yE_p(k+1|k) \\[1ex] 0 \\[1ex] \end{matrix} \right]}_b\\[1ex] &=Az-b \end{aligned}\tag{22}
ρ=[Γy(SxΔx(k)+Iyc(k)+SdΔd(k)+SuΔU(k)−R(k+1))ΓuΔU(k)]=[ΓySuΓu]ΔU(k)−
Γy(R(k+1)−SxΔx(k)−Iyc(k)−SdΔd(k))
Ep(k+1∣k)0
=Az
[ΓySuΓu]ΔU(k)−b
[ΓyEp(k+1∣k)0]=Az−b(22)
上式中
z
=
Δ
U
(
k
)
,
A
=
[
Γ
y
S
u
Γ
u
]
,
b
=
[
Γ
y
E
p
(
k
+
1
∣
k
)
0
]
E
p
(
k
+
1
∣
k
)
=
R
(
k
+
1
)
−
S
x
Δ
x
(
k
)
−
I
y
c
(
k
)
−
S
d
Δ
d
(
k
)
(23)
\begin{aligned} &z=\Delta U(k),\quad A=\left[ \begin{matrix} \Gamma_y\cal{S}_u \\[1ex] \Gamma_u \\[1ex] \end{matrix} \right],\quad b=\left[ \begin{matrix} \Gamma_yE_p(k+1|k) \\[1ex] 0 \\[1ex] \end{matrix} \right]\\ &E_p(k+1|k)=R(k+1)-\cal{S}_x\Delta x(k)-\cal{I}y_c(k)-\cal{S}_d\Delta d(k)\tag{23} \end{aligned}
z=ΔU(k),A=[ΓySuΓu],b=[ΓyEp(k+1∣k)0]Ep(k+1∣k)=R(k+1)−SxΔx(k)−Iyc(k)−SdΔd(k)(23)
因此,无约束预测控制的开环优化问题变为
min
z
ρ
T
ρ
,
其中
ρ
=
A
z
−
b
(24)
\min_z\rho^T\rho,\quad其中\quad\rho=Az-b\tag{24}
zminρTρ,其中ρ=Az−b(24)
得极值解为
z
∗
=
(
A
T
A
)
−
1
A
T
b
(25)
z^\ast=(A^TA)^{-1}A^Tb\tag{25}
z∗=(ATA)−1ATb(25)
又由
d
(
ρ
T
ρ
)
d
z
2
=
2
A
T
A
>
0
(26)
\frac{\mathrm{d}(\rho^T\rho)}{\mathrm{d}z^2}=2A^TA>0\tag{26}
dz2d(ρTρ)=2ATA>0(26)
知(25)是取得最小值的解。将式(23)代入(25),得到优化问题的解,即
k
k
k 时刻的最优控制序列为
Δ
∗
U
(
k
)
=
(
S
u
T
Γ
y
T
Γ
y
S
u
+
Γ
u
T
Γ
u
)
−
1
S
u
T
Γ
y
T
Γ
y
E
p
(
k
+
1
∣
k
)
(27)
\Delta^\ast U(k)=({\cal{S}}_u^T\Gamma_y^T\Gamma_y{\cal{S}_u}+\Gamma_u^T\Gamma_u)^{-1}{\cal{S}}_u^T\Gamma_y^T\Gamma_yE_p(k+1|k)\tag{27}
Δ∗U(k)=(SuTΓyTΓySu+ΓuTΓu)−1SuTΓyTΓyEp(k+1∣k)(27)
其中 E p ( k + 1 ∣ k ) E_p(k+1|k) Ep(k+1∣k) 由(23)计算。
注意:本节讨论的是预测控制基本原理的第二个步骤:(数值)求解优化问题。由于我们采用的预测模型是线性的,目标函数是二次型的,且没有考虑时域硬约束,因此,可以得到优化问题的解析解,无须采用数值方法求解。
3.3、预测控制闭环解
根据模型预测控制的基本原理,只有开环最优控制序列的第一个元素将作用于系统(即预测控制基本原理的第三个步骤:优化解的第一个元素作用于系统),即
Δ
u
(
k
)
=
[
I
n
u
×
n
u
0
⋯
0
]
1
×
m
Δ
U
∗
(
k
)
=
[
I
n
u
×
n
u
0
⋯
0
]
1
×
m
(
S
u
T
Γ
y
T
Γ
y
S
u
+
Γ
u
T
Γ
u
)
−
1
S
u
T
Γ
y
T
Γ
y
E
p
(
k
+
1
∣
k
)
\begin{aligned} \Delta u(k)&=\left[ \begin{matrix} \ \ I_{n_u\times n_u} &0 &\cdots &0\ \ \end{matrix} \right]_{1\times m}\Delta U^\ast(k)\\ &=\left[ \begin{matrix} \ \ I_{n_u\times n_u} &0 &\cdots &0\ \ \end{matrix} \right]_{1\times m}({\cal{S}}_u^T\Gamma_y^T\Gamma_y{\cal{S}_u}+\Gamma_u^T\Gamma_u)^{-1}{\cal{S}}_u^T\Gamma_y^T\Gamma_yE_p(k+1|k) \end{aligned}
Δu(k)=[ Inu×nu0⋯0 ]1×mΔU∗(k)=[ Inu×nu0⋯0 ]1×m(SuTΓyTΓySu+ΓuTΓu)−1SuTΓyTΓyEp(k+1∣k)
定义预测控制增益
K
m
p
c
=
[
I
n
u
×
n
u
0
⋯
0
]
1
×
m
(
S
u
T
Γ
y
T
Γ
y
S
u
+
Γ
u
T
Γ
u
)
−
1
S
u
T
Γ
y
T
Γ
y
(28)
K_{mpc}=\left[ \begin{matrix} \ \ I_{n_u\times n_u} &0 &\cdots &0\ \ \end{matrix} \right]_{1\times m}({\cal{S}}_u^T\Gamma_y^T\Gamma_y{\cal{S}_u}+\Gamma_u^T\Gamma_u)^{-1}{\cal{S}}_u^T\Gamma_y^T\Gamma_y\tag{28}
Kmpc=[ Inu×nu0⋯0 ]1×m(SuTΓyTΓySu+ΓuTΓu)−1SuTΓyTΓy(28)
那么,控制增量可由下式计算:
Δ
u
(
k
)
=
K
m
p
c
E
p
(
k
+
1
∣
k
)
(29)
\Delta u(k)=K_{mpc}E_p(k+1|k)\tag{29}
Δu(k)=KmpcEp(k+1∣k)(29)
其中 E p ( k + 1 ∣ k ) E_p(k+1|k) Ep(k+1∣k) 由(23)在线计算。显然,如果加权矩阵 Γ y \Gamma_y Γy 和 Γ u \Gamma_u Γu 是与时间无关的常数,则 K m p c K_mpc Kmpc 可以由(28)离线计算。在 k + 1 k+1 k+1 时刻,得到新的测量值 x ( k + 1 ) x(k+1) x(k+1),将由预测方程(9)重新计算系统未来的输出,并且由(27)计算最优控制序列 Δ U ∗ ( k + 1 ) \Delta U^\ast(k+1) ΔU∗(k+1)。最后,由预测控制基本原理中的”滚动时域,重复进行“的机制,给出无约束预测控制的算法如下。
无约束预测控制算法
- (1) 初始化:设定预测时域 p p p 和控制时域 m m m,初始值 u ( − 1 ) = 0 , x ( − 1 ) = 0 u(-1)=0,x(-1)=0 u(−1)=0,x(−1)=0;由(10)计算 S x , I , S d \cal{S_x},I,S_d Sx,I,Sd 和 S u \cal S_u Su,由(28)计算 K m p c K_{mpc} Kmpc。
- (2) k ≥ 0 k\geq 0 k≥0 时刻,得到测量值 x ( k ) x(k) x(k) 和 d ( k ) d(k) d(k)。由(1)计算 y c ( k ) y_c(k) yc(k);计算 Δ x ( k ) = x ( k ) − x ( k − 1 ) \Delta x(k)=x(k)-x(k-1) Δx(k)=x(k)−x(k−1)。
- (3) 由(23)计算误差 E p ( k + 1 ∣ k ) E_p(k+1|k) Ep(k+1∣k)。
- (4) 由(29)计算控制量变化量 Δ u ( k ) \Delta u(k) Δu(k)。
- (5) 将 u ( k ) = u ( k − 1 ) + Δ u ( k ) u(k)=u(k-1)+\Delta u(k) u(k)=u(k−1)+Δu(k) 作用于系统。
- (6) 在 k + 1 k+1 k+1 时刻,测量 x ( k + 1 ) x(k+1) x(k+1) 和 d ( k + 1 ) d(k+1) d(k+1) 的值,并且令 k = k + 1 k=k+1 k=k+1,返回第(2)步。
下面仔细分析一下预测控制器(29)的结构。为此,将
y
c
(
k
)
=
C
c
x
(
k
)
y_c(k)=C_cx(k)
yc(k)=Ccx(k) 和
Δ
x
(
k
)
=
x
(
k
)
−
x
(
k
−
1
)
\Delta x(k)=x(k)-x(k-1)
Δx(k)=x(k)−x(k−1) 代入(23),推导得
E
p
(
k
+
1
∣
k
)
=
R
(
k
+
1
)
−
S
x
Δ
x
(
k
)
−
I
y
c
(
k
)
−
S
d
Δ
d
(
k
)
=
R
(
k
+
1
)
−
S
x
x
(
k
)
+
S
x
x
(
k
−
1
)
−
I
C
c
x
(
k
)
−
S
d
Δ
d
(
k
)
=
R
(
k
+
1
)
−
(
S
x
+
I
C
c
)
x
(
k
)
−
S
d
Δ
d
(
k
)
+
S
x
x
(
k
−
1
)
\begin{aligned} E_p(k+1|k)&=R(k+1)-\cal{S}_x\Delta x(k)-\cal{I}{y_c}(k)-\cal{S}_d\Delta d(k)\\[1ex] &=R(k+1)-{\cal{S}}_xx(k) + {\cal{S}}_xx(k-1)-{\cal{I}}C_cx(k)-\cal{S}_d\Delta d(k)\\[1ex] &=R(k+1)-({\cal{S}}_x+{\cal{I}}C_c)x(k)-\cal{S}_d\Delta d(k)+{\cal{S}}_xx(k-1) \end{aligned}
Ep(k+1∣k)=R(k+1)−SxΔx(k)−Iyc(k)−SdΔd(k)=R(k+1)−Sxx(k)+Sxx(k−1)−ICcx(k)−SdΔd(k)=R(k+1)−(Sx+ICc)x(k)−SdΔd(k)+Sxx(k−1)
将其代入(29),得
Δ
u
(
k
)
=
K
m
p
c
E
p
(
k
+
1
∣
k
)
=
K
m
p
c
R
(
k
+
1
)
−
K
m
p
c
(
S
x
+
I
C
c
)
x
(
k
)
−
K
m
p
c
S
d
Δ
d
(
k
)
+
K
m
p
c
S
x
x
(
k
−
1
)
\begin{aligned} \Delta u(k)&=K_{mpc}E_p(k+1|k)\\[1ex] &=K_{mpc}R(k+1)-K_{mpc}({\cal{S}}_x+{\cal{I}}C_c)x(k)-K_{mpc}{\cal{S}}_d\Delta d(k)+K_{mpc}{\cal{S}}_xx(k-1) \end{aligned}
Δu(k)=KmpcEp(k+1∣k)=KmpcR(k+1)−Kmpc(Sx+ICc)x(k)−KmpcSdΔd(k)+KmpcSxx(k−1)
上式中的各项具有一下解释:
(1)
K
m
p
c
R
(
k
+
1
)
K_{mpc}R(k+1)
KmpcR(k+1) 是基于未来参考输入的前馈补偿。
(2)
−
K
m
p
c
S
d
Δ
d
(
k
)
-K_{mpc}{\cal{S}}_d\Delta d(k)
−KmpcSdΔd(k) 是基于可测干扰的前馈补偿。
(3)
−
K
m
p
c
(
S
x
+
I
C
c
)
x
(
k
)
+
K
m
p
c
S
x
x
(
k
−
1
)
-K_{mpc}({\cal{S}}_x+{\cal{I}}C_c)x(k)+K_{mpc}{\cal{S}}_xx(k-1)
−Kmpc(Sx+ICc)x(k)+KmpcSxx(k−1) 是状态反馈补偿。值得注意的是,这里的反馈补偿不仅用到了当前时刻的状态值,还用到了前一时刻的状态值。
注:需要指出的是计算前馈控制量时用到了参考输入在预测时域内的所有值。因此,选择过长的预测时域可能会导致保守的控制动作。
6、单输入单输出例子
6.1 问题描述
在无限光滑的一维水平直线上有一个质量为
m
m
m 的滑块,初始位置和初始速度都为 0,现需要设计控制器,在传感器测得滑块位置
x
x
x 的基础上,为滑块提供外力
u
u
u,使其跟随参考点
x
r
=
1
x_r=1
xr=1。
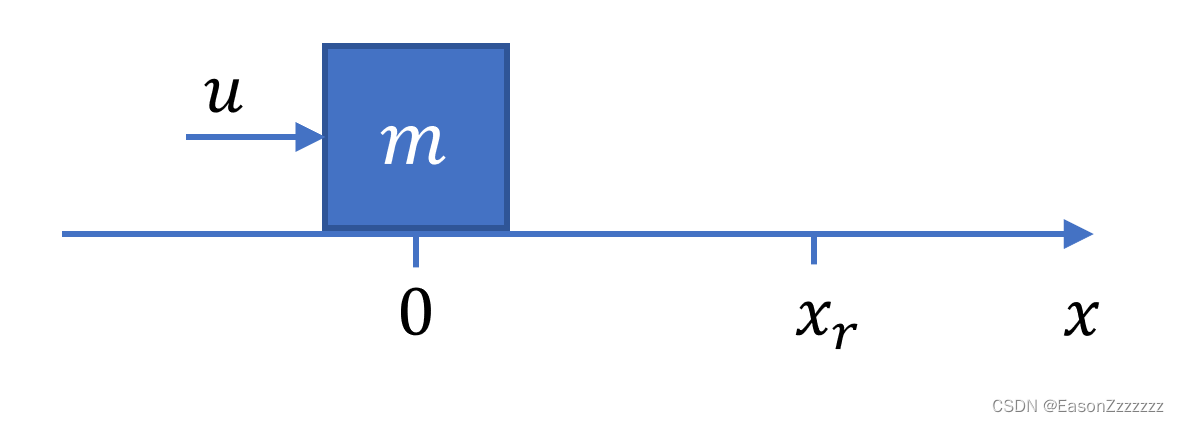
6.2 预测模型(连续时间模型)
首先建立动力学微分方程
x
¨
=
u
m
\ddot{x} = \frac{u}{m}
x¨=mu
选取状态向量
x
=
[
x
x
˙
]
x=\left[ \begin{matrix} \ x\\ \ \dot x \end{matrix} \right]
x=[ x x˙] (除非特殊说明,后文中
x
x
x 表示状态向量,而不是滑块位置)。
构建系统状态方程:
x
˙
=
A
c
x
(
t
)
+
B
c
u
u
(
t
)
y
c
(
t
)
=
C
c
x
(
t
)
\begin{aligned} \dot x &= A_cx(t)+B_{cu}u(t)\\[1ex] y_c(t)&=C_cx(t) \end{aligned}
x˙yc(t)=Acx(t)+Bcuu(t)=Ccx(t)
其中 A c = [ 0 1 0 0 ] , B c u = [ 0 1 m ] , C c = [ 1 0 ] A_c=\left[ \begin{matrix} \ 0&1\\[1ex] \ 0&0 \end{matrix} \right],B_{cu}=\left[ \begin{matrix} \ 0\\[1ex] \ \dfrac{1}{m} \end{matrix} \right],C_c=\left[ \begin{matrix} \ 1&0\\ \end{matrix} \right] Ac=[ 0 010],Bcu= 0 m1 ,Cc=[ 10]
6.3 预测模型(离散时间模型)
由(3),得
A
=
e
A
c
T
s
=
I
+
A
T
s
+
1
2
!
A
2
T
s
2
+
⋯
≈
[
1
T
s
0
1
]
B
u
=
∫
0
T
s
e
A
c
τ
d
τ
⋅
B
c
u
≈
[
0
T
s
m
]
\begin{aligned} A&=e^{A_cT_s}=I+AT_s+\frac{1}{2!}A^2{T_s}^2+\cdots\approx\left[ \begin{matrix} \ 1&T_s\\[1ex] \ 0&1 \end{matrix} \right]\\ B_u&=\int_0^{T_s}e^{A_c\tau}\mathrm{d}\tau\cdot B_{cu}\approx\left[ \begin{matrix} \ 0\\[1ex] \ \dfrac{T_s}{m} \end{matrix} \right] \end{aligned}
ABu=eAcTs=I+ATs+2!1A2Ts2+⋯≈[ 1 0Ts1]=∫0TseAcτdτ⋅Bcu≈
0 mTs
6.4 预测方程
Y p ( k + 1 ∣ k ) = S x Δ x ( k ) + I y c ( k ) + S d Δ d ( k ) + S u Δ U ( k ) Y_p(k+1|k)=S_x\Delta x(k)+{\cal{I}}y_c(k)+{\cal{S}_d}\Delta d(k)+{\cal{S}_u}\Delta U(k) Yp(k+1∣k)=SxΔx(k)+Iyc(k)+SdΔd(k)+SuΔU(k)
其中
S
x
=
[
C
c
A
∑
i
=
1
2
C
c
A
i
⋮
∑
i
=
1
p
C
c
A
i
]
p
×
1
,
I
=
[
I
n
c
×
n
c
I
n
c
×
n
c
⋮
I
n
c
×
n
c
]
p
×
1
,
S
d
=
[
C
c
B
d
∑
i
=
1
2
C
c
A
i
−
1
B
d
⋮
∑
i
=
1
p
C
c
A
i
−
1
B
d
]
p
×
1
,
S
u
=
[
C
c
B
u
0
0
⋯
0
∑
i
=
1
2
C
c
A
i
−
1
B
u
C
c
B
u
0
⋯
0
⋮
⋮
⋮
⋮
∑
i
=
1
m
C
c
A
i
−
1
B
u
∑
i
=
1
m
−
1
C
c
A
i
−
1
B
u
⋯
⋯
C
c
B
u
⋮
⋮
⋮
⋮
∑
i
=
1
p
C
c
A
i
−
1
B
u
∑
i
=
1
p
−
1
C
c
A
i
−
1
B
u
⋯
⋯
∑
i
=
1
p
−
m
+
1
C
c
A
i
−
1
B
u
]
p
×
m
\begin{aligned} S_x&=\left[ \begin{matrix} C_cA \\[2ex] \sum_{i=1}^2C_cA^i \\[2ex] \vdots\\[2ex] \sum_{i=1}^pC_cA^i \end{matrix} \right]_{p\times 1} ,\quad{\cal{I}}=\left[ \begin{matrix} I_{n_c\times n_c} \\[1ex] I_{n_c\times n_c} \\[1ex] \vdots\\[1ex] I_{n_c\times n_c} \end{matrix} \right]_{p\times 1},\quad{\cal{S}_d}=\left[ \begin{matrix} C_cB_d \\[2ex] \sum_{i=1}^2C_cA^{i-1}B_d \\[2ex] \vdots\\[2ex] \sum_{i=1}^pC_cA^{i-1}B_d \end{matrix} \right]_{p\times 1},\\[4ex] {\cal{S}_u}&=\left[ \begin{matrix} C_cB_u & 0 & 0 & \cdots & 0\\[2ex] \sum_{i=1}^2C_cA^{i-1}B_u & C_cB_u & 0 & \cdots & 0 \\[2ex] \vdots & \vdots & \vdots & &\vdots \\[2ex] \sum_{i=1}^mC_cA^{i-1}B_u & \sum_{i=1}^{m-1}C_cA^{i-1}B_u & \cdots & \cdots & C_cB_u \\[2ex] \vdots & \vdots & \vdots & &\vdots \\[2ex] \sum_{i=1}^pC_cA^{i-1}B_u & \sum_{i=1}^{p-1}C_cA^{i-1}B_u & \cdots & \cdots & \sum_{i=1}^{p-m+1}C_cA^{i-1}B_u \end{matrix} \right]_{p\times m} \end{aligned}
SxSu=
CcA∑i=12CcAi⋮∑i=1pCcAi
p×1,I=
Inc×ncInc×nc⋮Inc×nc
p×1,Sd=
CcBd∑i=12CcAi−1Bd⋮∑i=1pCcAi−1Bd
p×1,=
CcBu∑i=12CcAi−1Bu⋮∑i=1mCcAi−1Bu⋮∑i=1pCcAi−1Bu0CcBu⋮∑i=1m−1CcAi−1Bu⋮∑i=1p−1CcAi−1Bu00⋮⋯⋮⋯⋯⋯⋯⋯00⋮CcBu⋮∑i=1p−m+1CcAi−1Bu
p×m
6.5 优化求解
预测控制增益
K
m
p
c
=
[
I
n
u
×
n
u
0
⋯
0
]
1
×
m
(
S
u
T
Γ
y
T
Γ
y
S
u
+
Γ
u
T
Γ
u
)
−
1
S
u
T
Γ
y
T
Γ
y
K_{mpc}=\left[ \begin{matrix} \ \ I_{n_u\times n_u} &0 &\cdots &0\ \ \end{matrix} \right]_{1\times m}({\cal{S}}_u^T\Gamma_y^T\Gamma_y{\cal{S}_u}+\Gamma_u^T\Gamma_u)^{-1}{\cal{S}}_u^T\Gamma_y^T\Gamma_y
Kmpc=[ Inu×nu0⋯0 ]1×m(SuTΓyTΓySu+ΓuTΓu)−1SuTΓyTΓy
误差
E
p
(
k
+
1
∣
k
)
=
R
(
k
+
1
)
−
S
x
Δ
x
(
k
)
−
I
y
c
(
k
)
−
S
d
Δ
d
(
k
)
E_p(k+1|k)=R(k+1)-\cal{S}_x\Delta x(k)-\cal{I}y_c(k)-\cal{S}_d\Delta d(k)
Ep(k+1∣k)=R(k+1)−SxΔx(k)−Iyc(k)−SdΔd(k)
控制增量
Δ
u
(
k
)
=
K
m
p
c
E
p
(
k
+
1
∣
k
)
\Delta u(k)=K_{mpc}E_p(k+1|k)
Δu(k)=KmpcEp(k+1∣k)
























 1660
1660

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








