一,单位阶跃函数:
- 如图:
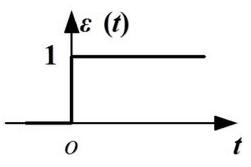 ,它有三个定义:
,它有三个定义: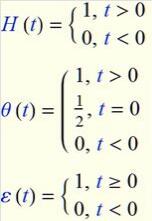
- 设
 为单位阶跃函数,那么
为单位阶跃函数,那么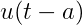 表示单位阶跃函数向右平移a个单位,如图:
表示单位阶跃函数向右平移a个单位,如图: 

二,单位方框函数:
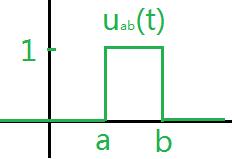

 如图:
如图: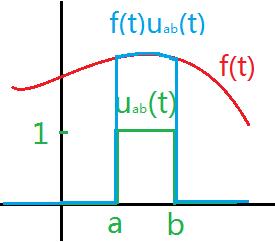
- 意义:去掉了
 在区间
在区间![[a,b]](https://i-blog.csdnimg.cn/blog_migrate/be62e9ac929e22aa27205b4c26e89e62.png) 以外的部分。
以外的部分。
三,单位阶跃函数的拉普拉斯变换:
![\mathcal {L}[u(t)]=\int_{0}^{\infty }u(t)e^{-st}dt](https://i-blog.csdnimg.cn/blog_migrate/6d52b422182f8789d220659198d60794.png)
- 因为当
 时,
时, ,所以:
,所以: ![\mathcal {L}[u(t)]=\int_{0}^{\infty }u(t)e^{-st}dt=\int_{0}^{\infty }e^{-st}dt=\frac{1}{s}](https://i-blog.csdnimg.cn/blog_migrate/2092ef2e40857d487f4e92a78e59960e.png) ,
,
![\mathcal {L}[1]=\frac{1}{s}](https://i-blog.csdnimg.cn/blog_migrate/c771631ffe87534b821d3f1a7d820810.png) (查表)
(查表)
四,逆变换的唯一性:
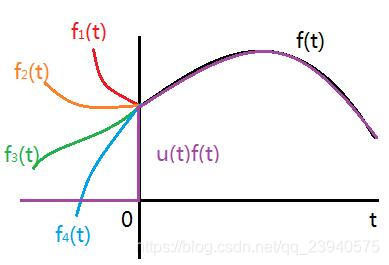
- 如图:
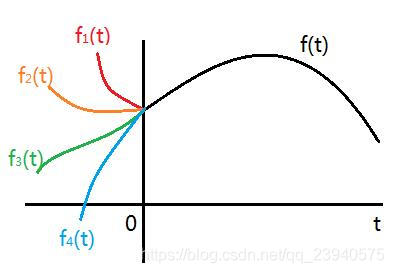
![\mathcal {L}[f_{1}(t)]=\mathcal {L}[f_{2}(t)]=\mathcal {L}[f_{3}(t)]=\mathcal {L}[f_{4}(t)]=\mathcal {L}[f(t)]=\int_{0}^{\infty }f(t)e^{-st}dt](https://i-blog.csdnimg.cn/blog_migrate/26787ee40918de66788d2972bd95874f.png)
- 因为拉普拉斯变换只关注
![\dpi{150} [0,\infty ]](https://i-blog.csdnimg.cn/blog_migrate/af700c76a11305208a25f6acb297e152.png) 这段区间,所以在这段区间内相等的函数,变换后的结果相等(无法区别)。
这段区间,所以在这段区间内相等的函数,变换后的结果相等(无法区别)。 - 那么:
![\mathcal {L}^{-1}[f(t)]=?](https://i-blog.csdnimg.cn/blog_migrate/de9344c0596d21229115c13f50809db8.png)
- 规定:
![\mathcal {L}^{-1}[f(t)]=u(t)\cdot f(t)](https://i-blog.csdnimg.cn/blog_migrate/a431a4d29394bbfd0bbce8641acbc10b.png)
- 如图:
五,延迟定理(t域平移定理):
![\mathcal {L}[f(t-a)]](https://i-blog.csdnimg.cn/blog_migrate/84380ef027bacd3ee05e283119525fac.png) (
( )不能用一个包含
)不能用一个包含![\mathcal {L}[f(t)]](https://i-blog.csdnimg.cn/blog_migrate/df887d5ecd6d8a2aa17377b3f7984ebe.png) 的式子表示
的式子表示- 为什么不能表示?
- 因为拉普拉斯变换只关注
![\dpi{150} [0,\infty ]](https://i-blog.csdnimg.cn/blog_migrate/af700c76a11305208a25f6acb297e152.png) 区间内的函数,如果
区间内的函数,如果 的区间是
的区间是![[-a,\infty ]](https://i-blog.csdnimg.cn/blog_migrate/6c821ea0a1fc55a0bc6050b5d6f65ded.png) ,那么向右平移a后会多出原负轴上的一段
,那么向右平移a后会多出原负轴上的一段 - 如图:
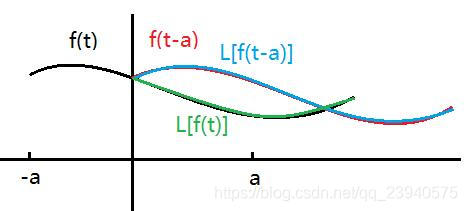
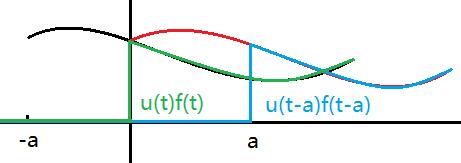
- 但是,如果乘上一个单位阶跃函数
 ,使当
,使当 时,
时,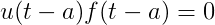
- 则以下延迟定理1成立:
![\mathcal {L}[u(t-a)f(t-a)]=e^{-as}F(s)=e^{-as}\mathcal {L}[f(t)]](https://i-blog.csdnimg.cn/blog_migrate/30c877db743eabbdce05d653adef4ba8.png)
- 如图:
- 另一个方便计算的等价公式——延迟定理2:
![\mathcal {L}[u(t-a)f(t)]=e^{-as}\mathcal {L}[f(t+a)]](https://i-blog.csdnimg.cn/blog_migrate/460c8b0c69870fbfecf19f33295b0328.png)
- 这时,可以和指数位移定律做个比较:
- 指数位移定律:
![\mathcal {L}[e^{at}\cdot u(t-a)f(t-a)]=F(s-a)](https://i-blog.csdnimg.cn/blog_migrate/bdfc4e12e433d137266877b6ecbe180e.png) ,见第十九讲第五节
,见第十九讲第五节
六,证明![\mathcal {L}[u(t-a)f(t-a)]=e^{-as}F(s)](https://i-blog.csdnimg.cn/blog_migrate/c5d692909c929ac30060d8c96763286e.png) :
:
![\mathcal {L}[u(t-a)f(t-a)]=\int_{0}^{\infty }e^{-st}u(t-a)f(t-a)dt](https://i-blog.csdnimg.cn/blog_migrate/d8bad92a2711b733d88ece0f40b7c53a.png)
- 设
 ,
,
- 则


- 因为当
 时,
时, ;当
;当 时,
时,
- 所以
![e^{-as}\int_{-a}^{\infty }e^{-st_{1}}u(t_{1})f(t_{1})dt_{1}=e^{-as}\int_{0}^{\infty }e^{-st_{1}}f(t_{1})dt_{1}=e^{-as}F(s)=e^{-as}\mathcal {L}[f(t)]](https://i-blog.csdnimg.cn/blog_migrate/147f6f3f100737a09739fe2159118cf9.png)
- 这里严重注意:
![\int_{0}^{\infty }e^{-st_{1}}f(t_{1})dt_{1}\neq \mathcal {L}[f(t_{1})]=\int_{0}^{\infty }e^{-st}f(t_{1})dt](https://i-blog.csdnimg.cn/blog_migrate/ed47ad0eb8a94a9d87f5864c39fb3c4c.png)
七,证明![\mathcal {L}[u(t-a)f(t)]=e^{-as}\mathcal {L}[f(t+a)]](https://i-blog.csdnimg.cn/blog_migrate/460c8b0c69870fbfecf19f33295b0328.png) :
:
- 已知
![\mathcal {L}[u(t-a)f(t-a)]=e^{-as}F(s)=e^{-as}\mathcal {L}[f(t)]](https://i-blog.csdnimg.cn/blog_migrate/30c877db743eabbdce05d653adef4ba8.png)
- 将
 替换
替换 :
: ![\mathcal {L}[u(t-a)f(t+a-a)]=e^{-as}\mathcal {L}[f(t+a)]](https://i-blog.csdnimg.cn/blog_migrate/fa4ef37e7dcd1c3c2246fed60d472556.png)
![\mathcal {L}[u(t-a)f(t)]=e^{-as}\mathcal {L}[f(t+a)]](https://i-blog.csdnimg.cn/blog_migrate/460c8b0c69870fbfecf19f33295b0328.png)
























 3386
3386

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








