什么是运动学奇异位型?
在初步系统地了解了机器人正逆运动学、雅可比矩阵相关知识后,下面来分析运动学的奇异性问题。
准备知识:
机器人学回炉重造(2-2):雅可比矩阵的求法——矢量积法、微分变换法、Manipulator Jacobian(Jacobian for short)
机械手微分运动方程中的雅可比矩阵揭示了关节速度
q
˙
\dot{\boldsymbol{q}}
q˙与末端执行器速度
v
e
=
[
p
˙
e
T
ω
e
T
]
T
\boldsymbol{v}_e = [\dot{\boldsymbol{p}}_e^T \quad \boldsymbol{\omega}_e^T]^T
ve=[p˙eTωeT]T之间的线性映射关系,这也是雅可比矩阵的核心定义。
v
e
=
J
(
q
)
q
˙
…
…
(
1
)
\boldsymbol{v}_e = \boldsymbol{J}(\boldsymbol{q})\dot{\boldsymbol{q}}……(1)
ve=J(q)q˙……(1)
通常情况下,雅可比矩阵是位型
q
\boldsymbol{q}
q(关节变量)的函数,那些使雅可比矩阵非满秩的位型被称为奇异位型。研究机械手奇异位型意义重大,原因如下:
a) 当机械手处于奇异位型时,会出现自由度缺失的情况,末端执行器的灵活性变差;
b) 当机械手处于奇异位型时,逆运动学问题可能出现无穷解;
c) 当接近奇异位型时,操作空间中细微的速度会导致关节空间中出现很大的速度。
机械手的奇异位型主要分为两种:(1)边界奇异位型,出现在机械手工作空间的边界,可通过阻止机械手运动到可达空间的边界来避免出现这种情况;(2)内部奇异位型,出现在机械手工作空间内,通常是由于两个或两个以上的关节轴重合导致,或者是由特定的末端执行器构型所导致,这种情况很危险,遇到的可能性较大。
例子:平面二连杆机械手的奇异位型

经过分析,可计算得到平面二连杆机械手的雅可比矩阵为
J
=
[
−
a
1
s
1
−
a
2
s
12
−
a
2
s
12
a
1
c
1
+
a
2
c
12
a
2
c
12
]
…
…
(
2
)
\boldsymbol{J} = \begin{bmatrix} -a_1s_1 - a_2s_{12} & -a_2s_{12} \\ a_1c_1 + a_2c_{12} & a_2c_{12} \end{bmatrix}……(2)
J=[−a1s1−a2s12a1c1+a2c12−a2s12a2c12]……(2)
矩阵行列式为
d
e
t
(
J
)
=
a
1
a
2
s
2
…
…
(
3
)
det(\boldsymbol{J}) = a_1a_2s_2……(3)
det(J)=a1a2s2……(3)
因为
a
1
,
a
2
≠
0
a_1,a_2 \neq 0
a1,a2=0,因此很容易看出当
θ
2
=
0
\theta_2 = 0
θ2=0或者
θ
2
=
π
\theta_2 = \pi
θ2=π时机械手处于奇异构型,这两个均是边界奇异位型。
奇异位型解耦
在机械手结构复杂的情况下,通过分析雅可比矩阵行列式来求内部奇异位型就显得比较困难。在分析了部分机械手的逆运动学问题后,可以看出,对于具有球腕结构的机械手而言,可以将其奇异位型计算分割为两个问题:
- 由前三个或三个以上连杆运动带来的手臂奇异位型计算;
- 由腕部关节运动带来的腕部奇异位型计算。
为了简单起见,考虑机械手的总自由度
n
=
6
n = 6
n=6,其雅可比矩阵可划分为四个
3
×
3
3 \times 3
3×3块矩阵,如下所示
J
=
[
J
11
J
12
J
21
J
22
]
…
…
(
4
)
\boldsymbol{J} = \begin{bmatrix} \boldsymbol{J}_{11} & \boldsymbol{J}_{12} \\ \boldsymbol{J}_{21} & \boldsymbol{J}_{22} \end{bmatrix}……(4)
J=[J11J21J12J22]……(4)
其中,由于后三个关节(已知为球腕)均为旋转关节,可以得到式(4)中右边两个块矩阵分别为
J
12
=
[
z
3
×
(
p
e
−
p
3
)
z
4
×
(
p
e
−
p
4
)
z
5
×
(
p
e
−
p
5
)
]
J
22
=
[
z
3
z
4
z
5
]
…
…
(
5
)
\boldsymbol{J}_{12} = \begin{bmatrix} \boldsymbol{z}_3 \times(\boldsymbol{p_e - \boldsymbol{p}_3}) & \boldsymbol{z}_4 \times(\boldsymbol{p_e - \boldsymbol{p}_4}) & \boldsymbol{z}_5 \times(\boldsymbol{p_e - \boldsymbol{p}_5}) \end{bmatrix}\\ \boldsymbol{J}_{22} = \begin{bmatrix} \boldsymbol{z_3} & \boldsymbol{z_4} & \boldsymbol{z_5} \end{bmatrix}……(5)
J12=[z3×(pe−p3)z4×(pe−p4)z5×(pe−p5)]J22=[z3z4z5]……(5)
由于奇异位型是机械结构的典型特征,并不会因为运动学坐标系选择的不同而不同(这句话超级重要!!!),因此将末端执行器的坐标系选在腕部轴线的交叉处显得更为方便简单,如下图所示,即将末端执行器坐标系{6}移到前面{3}、{4}、{5}的原点处,这是雅可比行列式简化计算的方法。可得到

J
12
=
[
0
0
0
]
…
…
(
6
)
\boldsymbol{J}_{12} = \begin{bmatrix} 0 & 0 & 0 \end{bmatrix}……(6)
J12=[000]……(6)
在这种情况下,机械手的雅可比矩阵变成了一个下三角矩阵,这就大大简化了行列式计算的过程,也就是对角线两个矩阵行列式相乘即可,如下
d
e
t
(
J
)
=
d
e
t
(
J
11
)
d
e
t
(
J
22
)
…
…
(
7
)
det(\boldsymbol{J}) = det(\boldsymbol{J}_{11})det(\boldsymbol{J}_{22})……(7)
det(J)=det(J11)det(J22)……(7)
综上,奇异位型解耦完成。上述行列式结果为0,有两种可能,第一,
d
e
t
(
J
11
)
=
0
det(\boldsymbol{J}_{11}) = 0
det(J11)=0,这个导致的是手臂奇异位型;第二,
d
e
t
(
J
22
)
=
0
det(\boldsymbol{J}_{22}) = 0
det(J22)=0,这个导致的是腕部奇异位型。可以看出,这种形式的雅可比矩阵并不能表示关节速度与末端执行器速度之间的关系,但这能够简化奇异位型的计算。下面详细讨论这两种可能的情况。
腕部奇异位型

基于上文奇异位型解耦,通过观察式(5)可以确定腕部奇异位型。当单位向量 z 3 z_3 z3、 z 4 z_4 z4、 z 5 z_5 z5线性相关时,可认为腕部处于某个奇异位型上。进一步可以发现,当 z 3 z_3 z3和 z 5 z_5 z5对齐时,腕部就处在奇异位型上,此时 θ 5 = 0 \theta_5 = 0 θ5=0或者 θ 5 = π \theta_5 = \pi θ5=π,上图即为第一种情况( θ 5 = 0 \theta_5 = 0 θ5=0)。可以看出,关于 θ 4 \theta_4 θ4和 θ 6 \theta_6 θ6的大小相等方向相反的旋转并不能使得末端执行器产生旋转,正因如此造成了自由度的缺失。更进一步地,该腕部无法产生绕垂直于 z 4 z_4 z4和 z 3 z_3 z3轴线的运动。这个奇异位型在关节空间中非常自然地产生,并且能够在操作臂可达空间中的任意位置遇到,需要额外注意。
手臂奇异位型

考虑上图所示拟人臂的奇异位型,计算得到该构型的雅可比矩阵为
J
=
[
−
s
1
(
a
2
c
2
+
a
3
c
23
)
−
c
1
(
a
2
s
2
+
a
3
s
23
)
−
a
3
c
1
s
23
c
1
(
a
2
c
2
+
a
3
c
23
)
−
s
1
(
a
2
s
2
+
a
3
s
23
)
−
a
3
s
1
s
23
0
a
2
c
2
+
a
3
c
23
a
3
c
23
0
s
1
s
1
0
−
c
1
−
c
1
1
0
0
]
…
…
(
8
)
\boldsymbol{J} = \begin{bmatrix} -s_1(a_2c_2 + a_3c_{23}) & -c_1(a_2s_2 + a_3s_{23}) & -a_3c_1s_{23} \\ c_1(a_2c_2 +a_3c_{23}) & -s_1(a_2s_2 + a_3s_{23}) & -a_3s_1s_{23} \\ 0 & a_2c_2 + a_3c_{23} & a_3c_{23} \\ 0 & s_1 & s_1 \\ 0 & -c_1 & -c_1 \\ 1 & 0 & 0 \end{bmatrix}……(8)
J=⎣⎢⎢⎢⎢⎢⎢⎡−s1(a2c2+a3c23)c1(a2c2+a3c23)0001−c1(a2s2+a3s23)−s1(a2s2+a3s23)a2c2+a3c23s1−c10−a3c1s23−a3s1s23a3c23s1−c10⎦⎥⎥⎥⎥⎥⎥⎤……(8)
可计算得到线性运动部分的雅可比矩阵行列式值为
d
e
t
(
J
v
)
=
−
a
2
a
3
s
3
(
a
2
c
2
+
a
3
c
23
)
…
…
(
9
)
det(\boldsymbol{J}_v) = -a_2a_3s_3(a_2c_2 + a_3c_{23})……(9)
det(Jv)=−a2a3s3(a2c2+a3c23)……(9)
可看出该行列式的值与第一个关节变量
θ
1
\theta_1
θ1无关。因为
a
2
a_2
a2和
a
3
a_3
a3不为零,因此当
s
3
=
0
s_3 = 0
s3=0亦或者
a
2
c
2
+
a
3
c
23
=
0
a_2c_2 + a_3c_{23} = 0
a2c2+a3c23=0时行列式值为零。考虑第一种情况,当
θ
3
=
0
\theta_3 = 0
θ3=0或
θ
3
=
π
\theta_3 = \pi
θ3=π时,如下图所示,此时拟人臂伸长或收缩,处于奇异位型,也称为肘部奇异位型,这种奇异位型在概念上等价于平面二连杆机械手的奇异位型。

从之前的拟人臂正运动学分析中可以看出(机器人学回炉重造(1-2):各种典型机械臂的正运动学建模(标准D-H法)),当腕关节点位于轴 z 0 z_0 z0上时,即此时 p x = p y = 0 p_x = p_y = 0 px=py=0,第二种情况就会发生,如下图所示,将其称为肩部奇异位型。在这种情况下, θ 1 \theta_1 θ1的旋转不会引起腕部位置的变化, J v \boldsymbol{J}_v Jv的第一列一直为空,而且此时逆运动学问题存在无穷解。另外,在该奇异位型下,腕部无法沿着 z 1 z_1 z1方向移动。
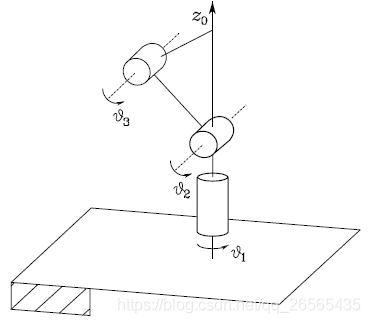
综上,与腕部奇异位型不同,手臂奇异位型在操作空间中可较容易被识别出来,故在轨迹规划阶段可适当避免该问题发生。
从线性方程的角度看,当机器人接近Singularity时,雅可比矩阵也越来越“病态”(ill-conditioned),很小的dx可能求得很大的dq,方程对数值误差也更加敏感;而当机器人处于Singularity时,线性方程可能无解、也可能有无数多个解。
下面的动图展示了控制机械臂运动轨迹通过两种常见的Singularity Configuration的情况,可以帮助你理解什么叫“接近Singularity时,很小的dx可能得到很大的dq”。(图中end effector走直线轨迹,它停顿的那一点就是机械臂处于singularity的点,可以看到在那个点关节突然快速运动)。以第二个动图为例,考虑拟人臂肩关节奇点的例子,可以看出指定给末端执行器的路径从基旋转轴附近经过(奇异位型的几何轨迹),基础关节将被迫在相对较短时间内旋转大约
π
\pi
π角度才能使末端执行器保持跟踪给定轨迹。因此当机械臂在运动时由于接近奇异位型而产生非常大的关节速度,常见的方法就是降低关节速度。

腕部奇异位型

手臂奇异位型
转载:6轴串联关节机器人的奇异点
六轴串联关节机器人有三种奇点:腕部奇点,肩部奇点,肘部奇点。
1、腕部奇点发生在4轴和6轴重合(平行)时。
2、肩部奇点发生在腕部中心位于1轴旋转中心线时。
3、肘部奇点发生在腕部中心和2轴3轴一条线 。
1. 4轴和6轴产生奇异点(wrist singularity)
下图中的六轴机器人,四轴和六轴相交[3](大部分机器人四轴和六轴都会相交,所以很多机器人都会存在这种奇异点,这玩意跟机器人的品牌无关,只和结构有关).
机器人的五轴与四轴和六轴的轴线相交,因此,机器人四,五,六三个轴便形成了上面提到的Gimbal Lock. 当五轴旋转到某个角度时,比如下面这个角度(所有的关节角度都是0°),四轴和六轴共线,奇异在此发生。当第4轴与第6轴共线,会造成系统尝试著将第4轴与第6轴瞬间旋转180度。


因此,在某系机器人仿真软件里,比如说ABB的robotstudio,当你打开机器人模型的时候,机器人的五轴会是这样的:

耷拉着小脑袋真不是为了卖萌,而是为了避开奇异点。
2.1轴和6轴奇异点(Alignment singularity)
当第1轴与腕关节中心C点(第5轴与第6轴之交点)共线,会造成系统尝试将第1轴与第4轴瞬间旋转180度。此类型有个特殊的情况,当第1轴与腕关节中心共线,且与第6轴共线时,会造成系统尝试第1轴与第6轴瞬间旋转180度,称之为Alignment Singularity (对齐奇异点)。
3.当机器人的2轴和3轴产生奇异点(Elbow singularity)

比如在当前的姿态下,机器人的端点可以产生的速度是由两个速度合成的:v1和v2.
v1是由于第一个旋转关节产生的;
v2是由于第二个旋转关节产生的;


图(a) 图(b)
可以看到图(a)中两个速度矢量v1和v2在平面上没有共线,它们是独立的、不共线的,我们是可以通过调整v1和v2的大小来得到任意的合速度的(大小和方向)。
但是,当机器人处于图(b)这个姿态的时候:这个情况很直接,无论你怎样改变v1和v2的大小,你都只能合成出和v1(v2)方向相同的速度。这就意味着你的机器人端点的速度不是任意的了,你只能产生某个方向上的速度。当腕关节中心C点与第2轴、第3轴共平面时,会造成肘关节卡住,像是被锁住一般,无法再移动。
这样机器人就奇异了。在机器人控制上来说,就意味着,你一旦奇异了,你就不能随意控制你的机器人朝着你想要的方向前进了。这也就是前面所谓的自由度退化、逆运动学无解。
解决办法:
1.在规划路径中尽可能的避免机器人经过奇异点。
2.结合机器人运动学,优化机器人反解算法,确保在奇异点附近伪逆解的稳定性 。
参考文献
Robotics - Modelling, Planning and Control
6轴串联关节机器人的奇异点
六轴机械手臂有哪些奇异点?

























 3万+
3万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










