【三维重建】三维重建学习笔记（1）—— 摄像机几何

第一章 摄像机几何

一、针孔摄像机和透镜

1. 针孔摄像机的原理

        如果将胶片直接放置在物体前方，物体的每一个点都会发散出很多束光线，胶片上的每一个点都会叠加物体不同位置发出的光线，这样没有办法在胶片上清晰地成像。

将胶片直接放置在物体前方

        如果在物体和胶片中间加一块隔板，隔板中间有一个小针孔，这样隔板会滤除大部分对成像产生干扰的光束，最后在胶片上呈现出一个倒立的像。这就是“小孔成像”原理的直观解释。

添加屏障以减少模糊

        针孔摄像机就利用了“小孔成像”原理，示意图如下：

针孔摄像机模型

         其中，f=焦距，o=光圈=针孔=摄像机中心。虚拟相平面与真实像平面对称，内容一样，x, y方向与真实相平面相反。实际处理中默认分析的是虚拟像平面。

        随着光圈减小，成像效果越来越清晰，但是图像越来越暗。为了解决这一问题，可以增加透镜，将多条光线聚焦到胶片上，增加照片的亮度。

凸透镜成像示意图​​​​

2. 近轴折射模型

        在凸透镜成像中，我们只关心透镜和胶片之间的距离\({z}'\)，其中\({z}'={{z}_{0}}+f\)。

近轴折射模型

        由上图可以看出，凸透镜成像与小孔成像满足同样的相似关系。因此，凸透镜成像满足以下关系：\[\left\{ \begin{align} & {x}'={z}'\frac{x}{z} \\ & {y}'={z}'\frac{y}{z} \\ \end{align} \right.\]

3. 镜头畸变问题

        由于镜头制造工艺不完美，镜头形状存在缺陷，因此相机成像会发生畸变。畸变主要分为径向畸变和切向畸变，这里主要考虑径向畸变。

        径向畸变可以分为枕形畸变和桶形畸变。通常情况下，广角镜头容易产生桶形畸变，而长焦镜头则更容易出现枕形畸变。

径向畸变示意图

二、摄像机几何

1. 数学基础

        图像点（欧式坐标→齐次坐标）：\[(x,y)\Rightarrow\left[\begin{matrix}x\\y\\1\\\end{matrix}\right]\]

        空间点（欧式坐标→齐次坐标）：\[(x,y,z)\Rightarrow\left[\begin{matrix}x\\y\\z\\1\\\end{matrix} \right]\]

        图像点（齐次坐标→欧式坐标）：\[\left[ \begin{matrix}x\\y\\w\\\end{matrix}\right]\Rightarrow (\frac{x}{w},\frac{y}{w})\]

        空间点（齐次坐标→欧式坐标）：\[\left[ \begin{matrix}x\\y\\z\\w\\\end{matrix}\right]\Rightarrow (\frac{x}{w},\frac{y}{w},\frac{z}{w})\]

        注意：如果两个齐次坐标成比例，如\(p=kq\)，则\(p\)和\(q\)对应的欧式坐标是相等的。

2. 相机坐标系（空间点）→像素坐标系的映射关系：

\[(x,y,z)=(fk\frac{x}{z}+{{c}_{x}},fl\frac{y}{z}+{{c}_{y}})\]

        其中，\(k\)和\(l\)单位：像素/米。通常令\(\alpha =fk,\beta =fl\)，单位：像素。

空间点到像素平面映射关系示意图

注意：

        实际标定中，相机坐系\(x\),\(y\)轴的方向是与像素坐标系\(u\),\(v\)轴的方向（注意：此处成像平面为虚拟像平面）相同的，而像素坐标系\(u\),\(v\)轴的方向是人为规定的，一般是左上角第一个像素为坐标原点，向右为\(u\)轴正方向，向下为\(v\)轴正方向。

        实际处理时都是使用虚拟像平面。虚拟像平面与像平面坐标系相比，\(x\), \(y\)轴反向。

        在上图中，假设相机与物体之间存在一个虚拟像平面，则像素坐标原点一般为从左向右观察到的虚拟相平面的左上角。

        设\({{P}_{h}}^{\prime }\)为像素点的齐次坐标，\({P}'\)为像素点的欧式坐标，\({{P}_{h}}\)为空间点相对于相机坐标系的齐次坐标，可以写出：\[{{P}_{h}}^{\prime }=\left[ \begin{matrix} \alpha x+{{c}_{x}}z  \\   \beta y+{{c}_{y}}z  \\   z  \\\end{matrix} \right]=\left[ \begin{matrix}   \alpha  & 0 & {{c}_{x}} & 0  \\   0 & \beta  & {{c}_{y}} & 0  \\   0 & 0 & 1 & 0  \\\end{matrix} \right]\left[ \begin{matrix}   x  \\   y  \\   z  \\   1  \\\end{matrix} \right]=\left[ \begin{matrix}   \alpha  & 0 & {{c}_{x}} & 0  \\   0 & \beta  & {{c}_{y}} & 0  \\   0 & 0 & 1 & 0  \\\end{matrix} \right]{{P}_{h}}\]

        当摄像机不存在偏斜时，摄像机的投影矩阵如上。但是实际中摄像机可能偏斜，如下图所示：

摄像机偏斜

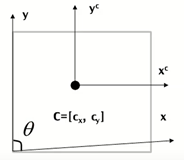
        当摄像机偏斜时，摄像机的投影矩阵定义为：\[{{P}_{h}}^{\prime }=\left[ \begin{matrix}   \alpha  & -\alpha \cot \theta  & {{c}_{x}} & 0  \\   0 & \frac{\beta }{\sin \theta } & {{c}_{y}} & 0  \\   0 & 0 & 1 & 0  \\\end{matrix} \right]\left[ \begin{matrix}   x  \\   y  \\   z  \\   1  \\\end{matrix} \right]\]

        由此可以定义摄像机内参数矩阵：\[K=\left[ \begin{matrix}   \alpha  & -\alpha \cot \theta  & {{c}_{x}}  \\   0 & \frac{\beta }{\sin \theta } & {{c}_{y}}  \\   0 & 0 & 1  \\\end{matrix} \right]\]

        因此，\({{P}_{h}}^{\prime }=K\left[ \begin{matrix}   I & 0  \\\end{matrix} \right]{{P}_{h}}\)。

3. 规范化投影变换

\[{{P}_{h}}^{\prime }=\left[ \begin{matrix}   1 & 0 & 0 & 0  \\   0 & 1 & 0 & 0  \\   0 & 0 & 1 & 0  \\\end{matrix} \right]\left[ \begin{matrix}   x  \\   y  \\   z  \\   1  \\\end{matrix} \right]\]

4. 世界坐标系→像素坐标系的映射关系： 

\[{{P}_{h}}^{\prime }=K\left[ \begin{matrix}   I & 0  \\\end{matrix} \right]{{P}_{h}}\text{=}K\left[ \begin{matrix}   I & 0  \\\end{matrix} \right]\left[ \begin{matrix}   R & T  \\   0 & 1  \\\end{matrix} \right]{{P}_{w}}=K\left[ \begin{matrix}   R & T  \\\end{matrix} \right]{{P}_{w}}=M{{P}_{w}}\]

        其中，\(K\)为相机的内参数，\(R\)和\(T\)为相机的外参数。\(K\)有5个自由度，\(R\)有3个自由度，\(T\)有三个自由度，故透视投影矩阵\(M\)有11个自由度。

5. 定理（Faugeras, 1993）

        假设\(M=K\left[ \begin{matrix}   R & T  \\\end{matrix} \right]=\left[ \begin{matrix}   KR & KT  \\\end{matrix} \right]=\left[ \begin{matrix}   A & b  \\\end{matrix} \right]\)，其中\(A=\left[ \begin{matrix}   {{a}_{1}}  \\   {{a}_{2}}  \\   {{a}_{3}}  \\\end{matrix} \right]\)。

        令\(M=\left[ \begin{matrix}   A & b  \\\end{matrix} \right]\)为3×4的矩阵，\({{a}_{i}}^{T}(i=1,2,3)\)表示矩阵\(A\)的行，则：

1. \(M\)是透视投影矩阵的一个充分必要条件是\(\text{Det}(A)\ne 0\)；
2. \(M\)是零倾斜透视投影矩阵的一个充分必要条件是\(\text{Det}(A)\ne 0\)且\(({{a}_{1}}\times {{a}_{3}})\cdot ({{a}_{2}}\times {{a}_{3}})=0\)；
3. \(M\)是零倾斜且宽高比为1（方形像素）的透视投影矩阵的一个充分必要条件是\(\text{Det}(A)\ne 0\)且：\[\left\{ \begin{align}  & ({{a}_{1}}\times {{a}_{3}})\cdot ({{a}_{2}}\times {{a}_{3}})=0 \\  & ({{a}_{1}}\times {{a}_{3}})\cdot ({{a}_{1}}\times {{a}_{3}})=({{a}_{2}}\times {{a}_{3}})\cdot ({{a}_{2}}\times {{a}_{3}}) \\ \end{align} \right.\]

6. 投影变换的性质

1. 点投影为点
2. 线投影为线
3. 近大远小
4. 角度不再保持
5. 平行线相交（3D世界中的平行线在图像中相交于“影消点”）

三、其他摄像机模型

1. 弱透视投影摄像机

        当相对场景深度小于其与相机的距离时，可以近似认为\(z\)保持不变。

弱透视投影摄像机

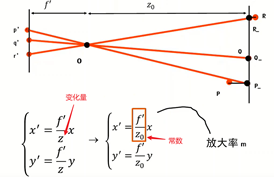
注意：

        弱透视投影摄像机的透视投影矩阵\(M\)的最后一行一定是0 0 0 1。

2. 正交投影摄像机

        当摄像机中心到像平面的距离无限远时，空间点和像平面点的坐标呈1:1的比例关系。

正交投影摄像机

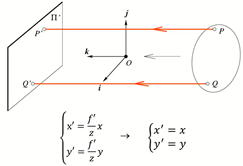
3. 透视投影摄像机和正交投影摄像机的比较

透视投影摄像机

正交投影摄像机

4. 各种摄像机模型的应用场合

• 正交投影：更多应用在建筑设计（AutoCAD）或者工业设计行业。
• 弱透视投影：在数学方面更简单。当物体较小且较远时准确，常用于图像识别任务。
• 透视投影：对于3D到2D映射的建模更为准确。用于运动恢复结构或SLAM。